-
1、下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2、如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成……那么第n个黑色L形的正方形个数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、有理数 , 在数轴上对应的位置如图,则下列结论不成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、如图,在中,B为上一点,连接 , 且 , , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如图,在网格中有一个以格点(网格线的交点)为顶点的 , 网格中的每个小正方形的边长都是1.
 (1)、作关于直线l对称的 .(2)、求的面积.
(1)、作关于直线l对称的 .(2)、求的面积. -
6、我们把按一定规律排列的一列数,称为数列,若对于一个数列中依次排列的相邻的三个数m、n、p,总满足 , 则称这个数列为理想数列.(1)、若数列 , , , , , , 是理想数列,则 , ;(2)、若数列 , , , , 是理想数列,求代数式的值;(3)、若数列…, , , , , 是理想数列,且 , 求代数式的值.
-
7、某服装店某员工周一的销售量恰好为每日标准销售量件,相比标准销售量,周二至周日销售量如下:件,件,件,件,件,件.(1)、周_____的销售量最高,这周的总销售量是________件.(2)、该服装店实行每日计件工资制,每销售一件可得30元,若超额完成任务,则超过部分每件另奖10元;少一件扣5元,当时,那么该售货员这一周的工资总额是多少元?
-
8、用代数式表示:(1)、的平方与的差;(2)、比的倒数与的倒数的和大的数;(3)、、两数的和与差的积;(4)、、两数的平方差除以、两数的和的平方所得的商.
-
9、计算:(1)、;(2)、;(3)、;(4)、 .
-
10、如图,在数轴上有若干个点,每相邻两个点之间的距离是一个单位长度,有理数、、、所表示的点是这些点中的个,且在数轴上的位置如图所示,已知 , 则 .

-
11、用表示不大于x的整数中的最大整数,如 , , 则 .
-
12、试写出一个含x的代数式 , 使得当时,代数式的值为 .
-
13、按要求取近似数(精确到).
-
14、若 , , 为整数,且 , 则的值为( )A、0 B、1 C、2 D、2024
-
15、根据世界食品物流组织()制定的要求,某种冷冻食品的标准储存温度是 , 下列四个储藏室的温度中不适合储藏这种冷冻食品的是( )A、 B、 C、 D、
-
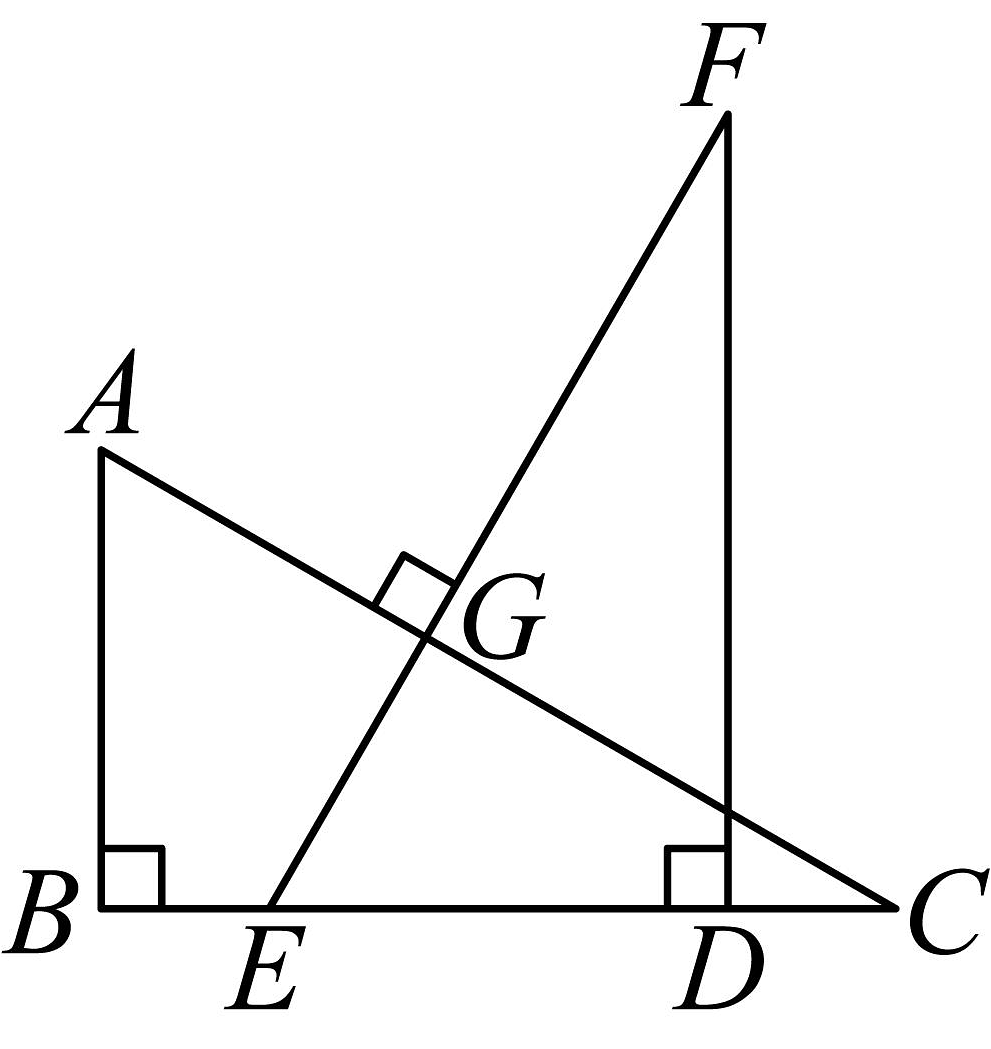
16、如图, 已知:AB⊥BC于B , EF⊥AC于G , DF ⊥BC于D , BC=DF.求证:AC=EF.
-
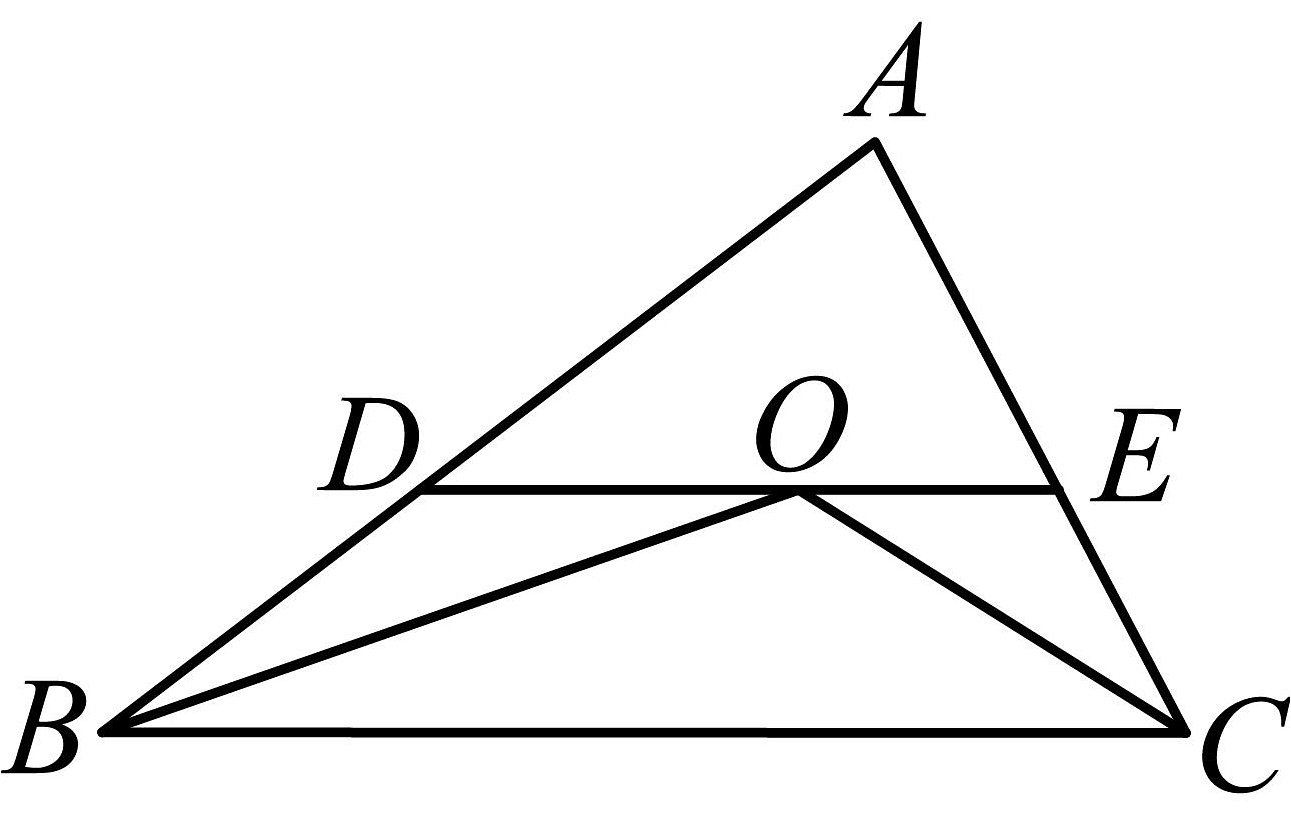
17、如图,中,点是与的平分线的交点,过作与平行的直线分别交、于、 . 已知的周长为15,的长为6,求的周长.
-
18、如图:
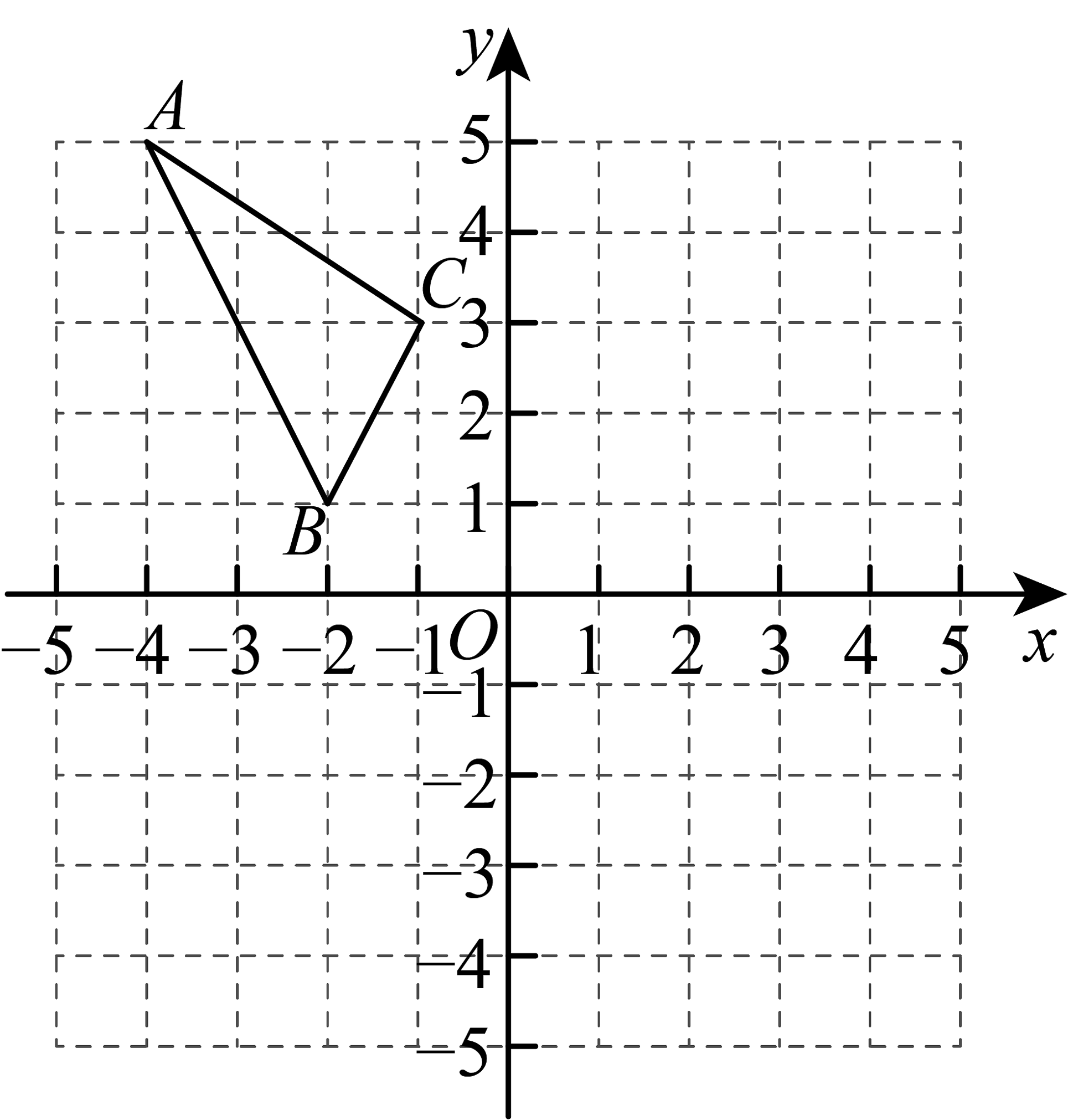 (1)、画出关于轴对称的;(2)、求的面积;(3)、在轴上找出点 , 使得最小.
(1)、画出关于轴对称的;(2)、求的面积;(3)、在轴上找出点 , 使得最小. -
19、已知中
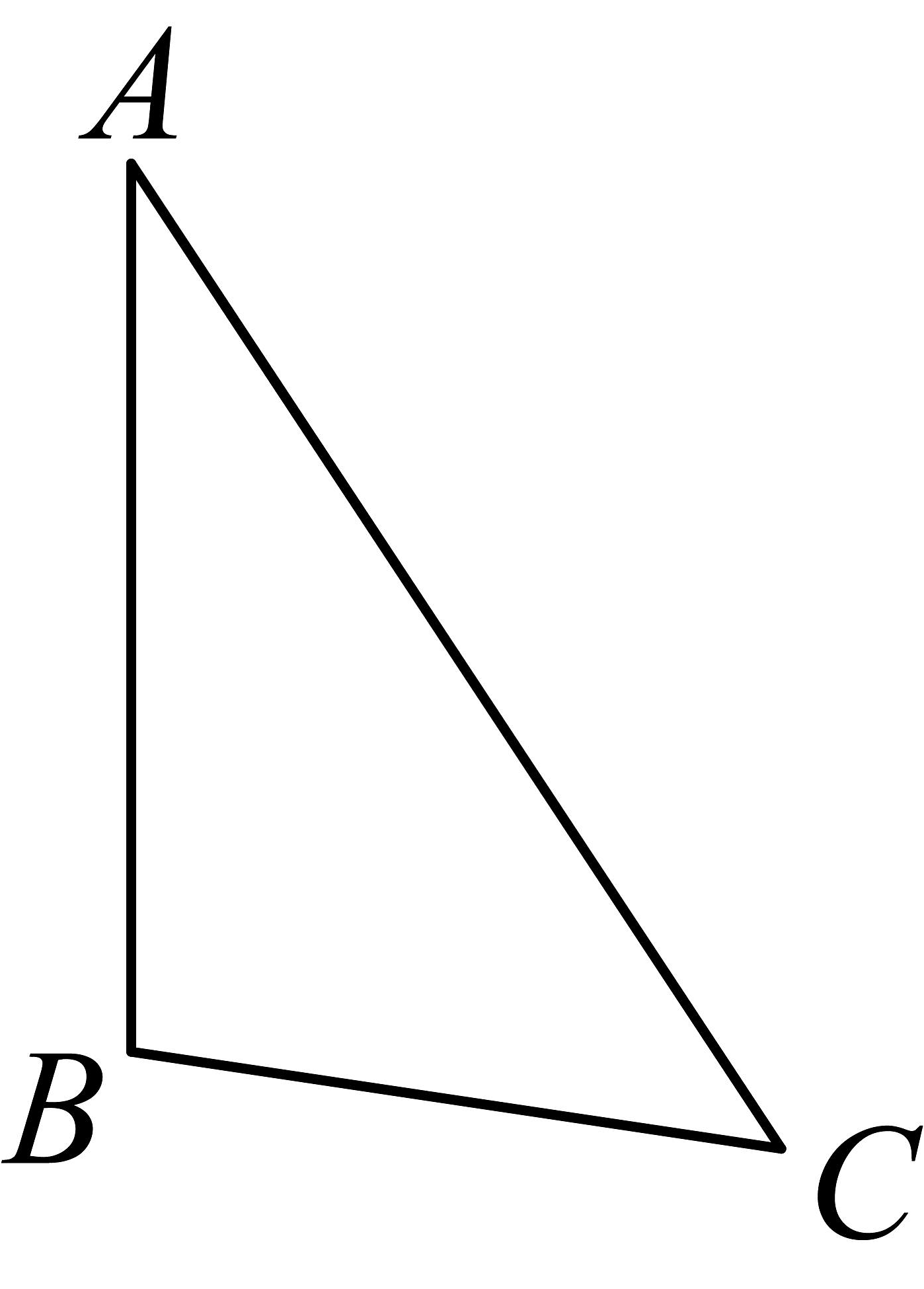 (1)、作的垂直平分线交于点 . (用尺规作图,保留作图痕迹)(2)、连接 . 若 , 求的度数.
(1)、作的垂直平分线交于点 . (用尺规作图,保留作图痕迹)(2)、连接 . 若 , 求的度数. -
20、如图,且 , , , 求的长度.
