相关试卷

1、如果水平面升高 $8 m$ 时水位变化记作 $+ 8 m$ ，那么水平面下降 $5 m$ 时水位变化记作（　　）

A、 $- 8 m$ B、 $+ 8 m$ C、 $- 5 m$ D、 $+ 5 m$

查看解析
2、比较大小：3 $\sqrt{7}$ ．（填“ $>$ ”“ $=$ ”或“ $<$ ”）

查看解析
3、已知数轴上A、B两点表示的数分别为a、b，且a、b满足 $|a + 9| + {(b - 6)}^{2} = 0$ ．点P沿数轴从A出发以n个单位长度/秒的速度向右匀速运动．

(1)、求a与b的值；

(2)、若5秒后，点P到点A的距离是点P到点B距离的2倍，求此时点P运动的速度；

(3)、在点P运动2秒后，点Q从点B出发以m个单位长度/秒的速度向左匀速运动，又经过4秒后，P、Q两点之间的距离为1，求m和n之间的数量关系．

查看解析
4、为了加强公民的节水意识，合理利用水资源，某市采取价格调控手段以达到节水的目的，下表是该市自来水收费价格的价目表．注：水费按月结算．
每月用水量
单价（单位：元 $/ m^{3}$ ）
不超过 $5 m^{3}$ 的部分
2
超过 $5 m^{3}$ 但不超过 $10 m^{3}$ 的部分
4
超过 $10 m^{3}$ 的部分
8

(1)、若某户居民2月份用水 $4 m^{3}$ ，求该月应缴纳水费多少元？

(2)、若某户居民3月份用水 $a (5 < a < 10) m^{3}$ ，则该用户3月份应缴纳水费多少元？（用含 $a$ 的代数式表示，并化简）

(3)、若某户居民4，5月份共用水 $10 m^{3}$ （5月份用水量多于4月份），设4月份用水 $x m^{3}$ 求该户居民4，5月份共缴纳水费多少元？（用含 $x$ 的代数式表示，并化简）．

查看解析
5、某校体育组需添置一批体育器材，包括足球50个；跳绳 $x$ 条（ $x > 50$ ）．已知某品牌足球每个统一定价为110元，跳绳每条统一定价为20元．现有 $A$ 、 $B$ 两家商店提出了各自的优惠方案：
$A$ 店：买一个足球送一条跳绳；
$B$ 店：足球和跳绳都打9折．

(1)、分别在 $A$ ， $B$ 两家商店购买，各需付款多少元？（用含 $x$ 的代数式表示，并化简）

(2)、当 $x = 300$ 时，
①通过计算说明此时在哪家商店购买较为合算？
②你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并计算共需付款多少元．

查看解析
6、如图，现有5张卡片上面分别各标注了一个数，请你仅使用“＋，－，×，÷”4种运算符号，将这5张卡片上的数全部连起来，组合成一个式子，使其计算结果为一个有理数，请你写出这个式子，并计算出结果．注：4种运算不一定全都用到，可使用括号．

查看解析
7、先化简，再求值： $3 (3 x - 2 y) - (6 x - 4 y - 1) + 3 x - 2 y$ ，其中 $x = \frac{2}{3}$ ， $y = \frac{3}{2}$ ．

查看解析
8、请选择你觉得最好的方法进行计算：

(1)、 $- 29 \frac{8}{9} \times 9$ ．

(2)、 $- 4 \times (- \frac{11}{6}) + 13 \times (- \frac{11}{6}) - 9 \times (- \frac{11}{6})$ ．

查看解析
9、请你将 $- 3$ ， $\sqrt{\frac{1}{4}}$ ， ${(- 2)}^{2}$ ， $- (- 1)$ ， $\sqrt[3]{27}$ 在数轴上表示出来，并用“ $<$ ”将上列各数连接起来．

查看解析
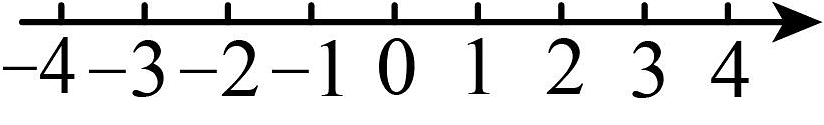
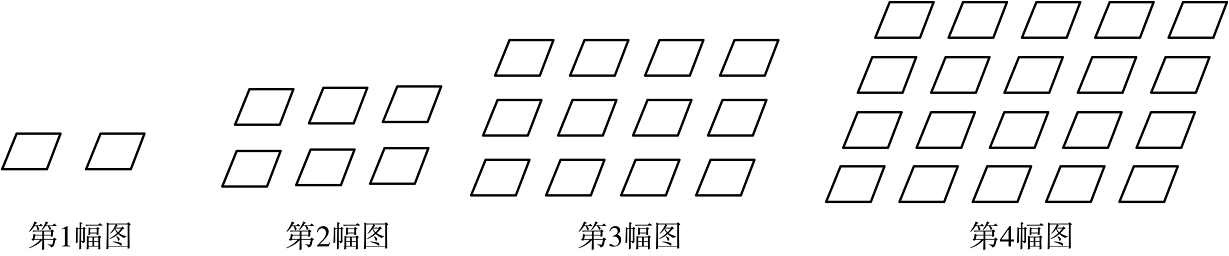
10、如图所示，将形状大小完全相同的“ $▱$ ”按照一定规律摆成下列图形，第1幅图中“ $▱$ ”的个数为 $a_{1}$ ，第2幅图中“ $▱$ ”的个数为 $a_{2}$ ，第3幅图中“ $▱$ ”的个数为 $a_{3}$ ， $\dots$ ．则 $\frac{2}{a_{1}} + \frac{2}{a_{2}} + \frac{2}{a_{3}}$ 的值为， $\frac{2}{a_{1}} + \frac{2}{a_{2}} + \dots + \frac{2}{a_{2023}} = \frac{n}{2024}$ ， $n$ 为正整数，则 $n$ 的值为．

查看解析
11、某公司去年每季度盈亏情况如下：“+”表示盈利，“-”表示亏损，单位：万元．第一季度 $- 1.5$ ；第二季度 $+ 1$ ；第三季度 $+ 1.3$ ，第四季度 $+ 3.2$ ，则这个公司去年一年共（填“盈利”或“亏损”）万元．

查看解析
12、以下各数：①0，② $\sqrt{8}$ ， ③﹣2，④ $\frac{π}{2}$ ， ⑤ $\sqrt{3}$ ， ⑥ $\frac{22}{7}$ ， ⑦0.1010010001…（相邻两个1之间依次增加一个0），其中是无理数的有．（只需填写序号）

查看解析
13、合并同类项： $3 a^{2} b - a^{2} b =$ ．

查看解析
14、若 $a$ 是最大的负整数， $b$ 是绝对值最小的数， $c$ 表示的数在原点左侧且距离原点3个单位长度，则 $a + b - c$ 的值为（）

A、2 B、 $- 2$ C、4 D、 $- 4$

查看解析
15、在 $- 1, + 7.5, 0, - \frac{2}{3}, - 0.9, 15$ 中，负数共有（）

A、1个 B、2个 C、3个 D、4个

查看解析
16、若分式 $\frac{m^{2} - 4}{- m + 2}$ 的值为0，则m的值为．

查看解析
17、若关于x的多项式 $x^{3} + 2 m x^{2} - 6 x^{2} - 7 x + 3$ 不含二次项，则m的值为．

查看解析
18、已知一次函数 $y = x + 1$ 的图象与二次函数 $y = x^{2} - b x + c$ 的图象相交于点 $A (- 1, 0)$ ， $B (4, n)$ ．

(1)、求二次函数的表达式；

(2)、结合图象，直接写出当 $x^{2} - b x + c > x + 1$ 时x的取值范围．

查看解析
19、如图，点A、B、C在⨀O上，∠ACB＝125°．请仅用无刻变的直尺分别按下列要求作图．
（1）在图（1）中，作一个度数为55°的圆周角；
（2）在图（2）中，作一个度数为35°的圆周角．

查看解析
20、解方程：

(1)、 $x^{2} + 2 x = 0$

(2)、 $4 x (2 x + 1) = 3 (2 x + 1)$

查看解析

上一页 1102 1103 1104 1105 1106 下一页跳转

每月用水量	单价（单位：元 $/ m^{3}$ ）
不超过 $5 m^{3}$ 的部分	2
超过 $5 m^{3}$ 但不超过 $10 m^{3}$ 的部分	4
超过 $10 m^{3}$ 的部分	8