-
1、计算下列各题.(1)、;(2)、;(3)、 .
-
2、如图是一组有规律的图案.第1个图中有4个小黑点.第2个图中有7个小黑点,第3个图中有12个小黑点.第4个图中有19个小黑点.…、按此规律,第9个图中有个小黑点,第n个图中有个小黑点.(用含n的代数式表示)

-
3、如图,已知点C为线段上一点,、 , 点D、E分别是 , 的中点,则cm, cm.

-
4、如图,将绕点C顺时针旋转得到 , 若 , 则°.

-
5、如图,数轴上 , 两点间的距离为 , 一动点从点出发,按以下规律跳动:第次跳动到的中点处,第次从点跳动到的中点处,第次从点跳动到的中点处按照这样的规律继续跳动到点 , , , 是正整数处,经过这样次跳动后的点所表示的数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、如下是嘉淇对一道题的解题过程:
……第①步
……第②步
. ……第③步
下列判断正确的是( )
A、第①步运用了乘法交换律 B、第②步运用了乘法对加法的分配律,但结果错误 C、第②步的运算结果正确 D、第③步的结果是本题的正确结果 -
7、如图,若 , 则下列结论正确的是( )
 A、 B、 C、 D、与的大小关系不确定
A、 B、 C、 D、与的大小关系不确定 -
8、综合与实践
【问题情境】
某综合实践小组进行废物再利用的环保小卫士行动,他们准备用废弃的宣传单制作长方体纸盒.
【操作探究】
(1)、若准备制作一个无盖的正方体纸盒,图1中的 图形经过折叠能围成无盖正方体纸盒.(2)、图2是嘉嘉的设计图,把它折成无盖正方体纸盒后与“保”字相对的是 字.(3)、如图3,有一张边长为的正方形废弃宣传单,嘉嘉准备将其四个角各剪去一个小正方形,折成无盖长方体纸盒,折成的纸盒高为 .①四角应各剪去边长为 的小正方形;
②计算此长方体纸盒的容积.
(4)、根据如图4方式制作一个有盖的长方体纸盒.方法:先在边长为的正方形纸板四角剪去两个边长为的小正方形和两个同样大小的小长方形,再沿虚线折叠起来.该长方体纸盒的体积为多少?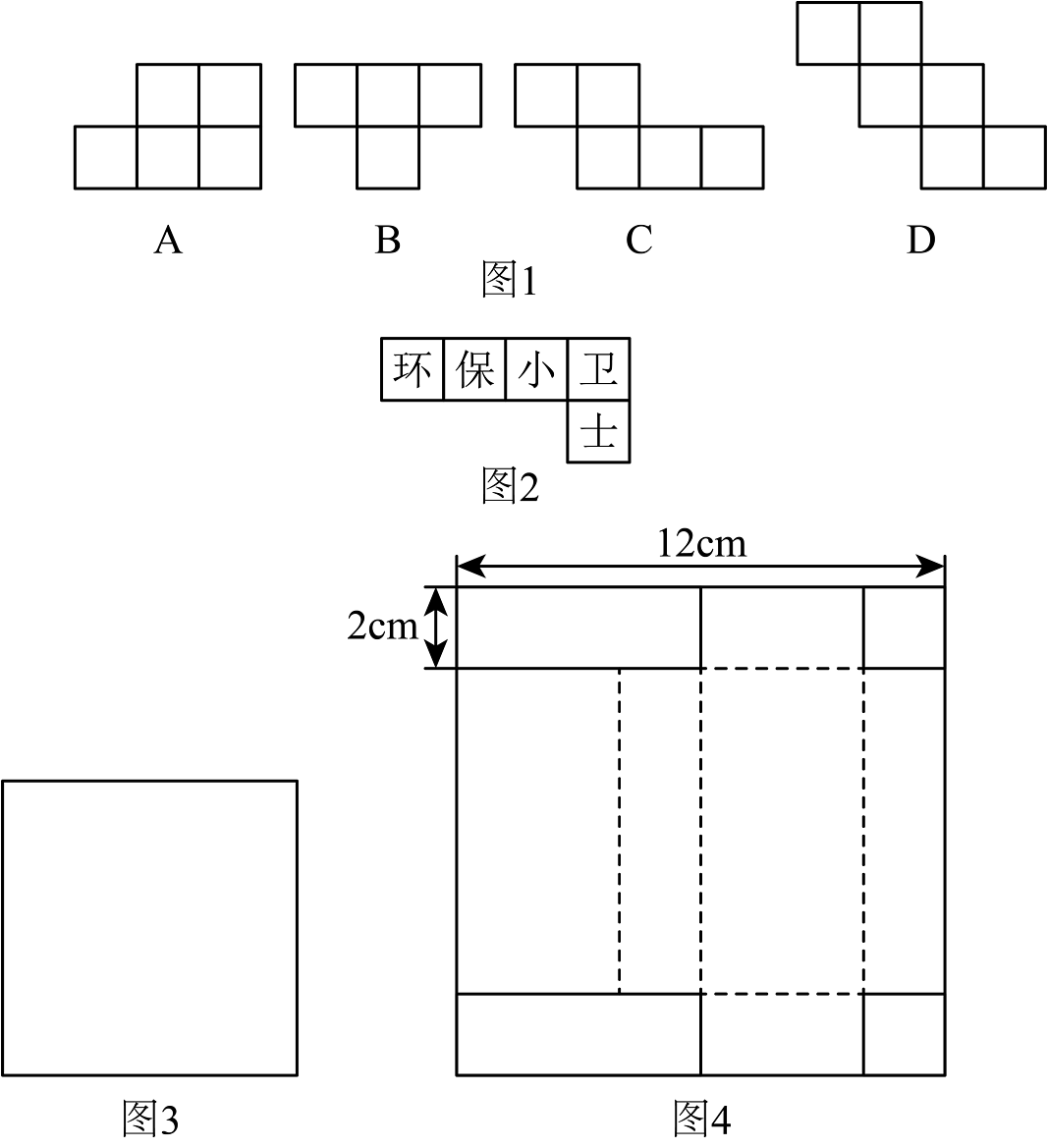
-
9、已知关于、的多项式 .(1)、求;老师展示了一位同学的作业如下:
解: 第一步
第二步
第三步
回答问题:这位同学第 步开始出现错误,错误原因是 ;
(2)、若的结果与字母的取值无关,求的值. -
10、化简并求值: , 其中x、y取值的位置如图所示.
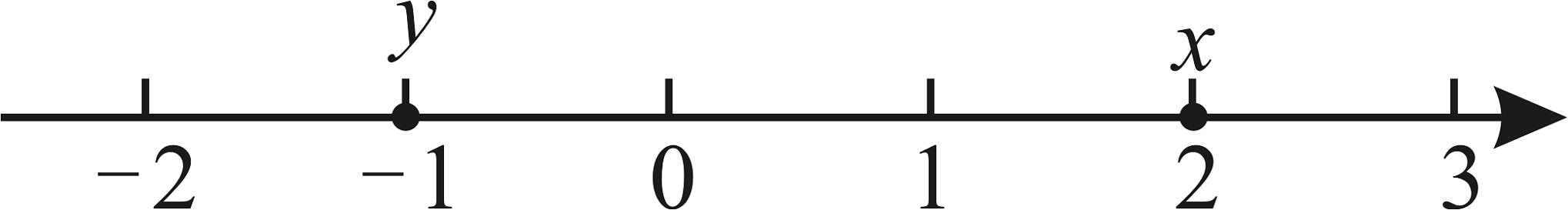
-
11、计算: .
-
12、已知 , 则 .
-
13、单项式的系数是 .
-
14、在某月的日历上用长方形圈到a,b,c,d四个数(如图),如果 , 那么的值为( )
 A、22 B、25 C、29 D、30
A、22 B、25 C、29 D、30 -
15、下列个数、、、、、每两个之间依次一个、 , 其中有理数有( )个A、3 B、4 C、5 D、6
-
16、在 , , , 这四个数中,最小的数是( )A、 B、 C、 D、
-
17、如图,直线 , 直线和被所截, , 则的长为( )
 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8 -
18、已知关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;(2)、当时,求出方程的解.
-
19、如图,⊙O的半径OA=1,B是⊙O上的动点(不与点A重合),过点B作⊙O的切线BC,BC=OA,连结OC,AC.当△OAC是直角三角形时,其斜边长为 .

-
20、已知点都在二次函数的图象上,则的大小关系是 .