相关试卷

1、如图，在正方形网格中， $△ A B C$ 各顶点都在格点上，点A的坐标为 $(- 5, 1)$ ，结合所给的平面直角坐标系解答下列问题：

(1)、画出 $△ A B C$ 绕点A顺时针旋转 $90 °$ 后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、画出 $△ A B C$ 关于原点O对称的 $△ A_{2} B_{2} C_{2}$ ；

(3)、点 $C_{1}$ 的坐标是；点 $C_{2}$ 的坐标是．

查看解析
2、如图，在每个小正方形的边长为1的网格中，点 $A$ ，点 $B$ ，点 $D$ 均在格点上，并且在同一个圆上，取格点 $M$ ，连接 $A M$ 并延长交圆于点 $C$ ．
（Ⅰ）四边形 $A B C D$ 外接圆的半径为．
（Ⅱ）请在如图所示的网格中，用无刻度的直尺画出线段 $A P$ ，使 $A P$ 平分 $∠ C A D$ ，且点 $P$ 在圆上，并简要说明点 $P$ 的位置是如何找到的（不要求证明）．

查看解析
3、若 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} + 4 x + 3 = 0$ 的两个根，则 $x_{1} x_{2}$ 的值是．

查看解析
4、如图，在△ABC中，∠CAB=65°，以点A为旋转中心，将△ABC绕点A逆时针旋转，得△AB^'C^' ，连接BB^' 若BB^' $∥$ AC，则旋转角的大小为（　　）．

A、35° B、40° C、50° D、65°

查看解析
5、已知一元二次方程 $x^{2} + k x + 3 = 0$ 有一个根为1，则k的值为（　　）

A、 $- 2$ B、 $- 4$ C、2 D、4

查看解析
6、下列图案中，是轴对称图形但不是中心对称图形的是（　　）

A、 B、 C、 D、

查看解析
7、如图，圆O为 $Rt △ A B C$ 的外接圆， $∠ A C B = 90 ° ， B C = 4 \sqrt{3}$ ， $A C = 4$ ，点D是圆O上的动点，且点C、D分别位于 $A B$ 的两侧．

(1)、求圆O的半径；

(2)、当 $C D = 4 \sqrt{2}$ 时，求 $∠ A C D$ 的度数；

(3)、设 $A D$ 的中点为M，在点D的运动过程中，线段 $C M$ 的最大值为．

查看解析
8、如图，已知二次函数 $y = a x^{2} + 2 x + c$ 的图象与x轴交于A，B两点，A点坐标为 $(- 1, 0)$ ，与y轴交于点 $C (0, 3)$ ．

(1)、求二次函数的表达式；

(2)、在直线 $B C$ 上方的抛物线上存在点Q，使得 $∠ Q C B = 2 ∠ A B C$ ，求点Q的坐标．

查看解析
9、阅读下列材料：
解方程： $x^{4} - 6 x^{2} + 5 = 0$ ．这是一个一元四次方程，根据该方程的特点，
它的解法通常是：
设 $x^{2} = y$ ，那么 $x^{4} = y^{2}$ ，于是原方程可变为 $y^{2} - 6 y + 5 = 0$ ①，
解这个方程得： $y_{1} = 1$ ， $y_{2} = 5$ ．
当 $y_{1} = 1$ 时， $x^{2} = 1$ ． ∴ $x = \pm 1$ ；当 $y_{2} = 5$ 时， $x^{2} = 5$ ， ∴ $x = \pm \sqrt{5}$
以原方程有四个根： $x_{1} = 1$ ， $x_{2} = - 1$ ， $x_{3} = \sqrt{5}$ ， $x_{4} = - \sqrt{5}$ ．
这个过程中，我们利用换元法达到降次的目的，体现了转化的数学思想．

(1)、用换元法解方程： ${(x^{2} - x)}^{2} - 4 (x^{2} - x) - 12 = 0$

(2)、 $Rt △ A B C$ 三边是 $a$ ， $b$ ， $c$ ，若两直角边 $a$ ， $b$ 满足 $(a + b) (a + b - 7) + 10 = 0$ ，斜边 $c = 4$ ，求 $Rt △ A B C$ 的面积．

查看解析
10、已知直线 $A B$ 与 $⊙ O$ 相切于点 $B$ ，连接 $O A$ 交 $⊙ O$ 于点 $C$ ．
（1）如图①，点 $D$ 是优弧 $B C$ 上一点，连接 $C D, B D$ ，若 $∠ C D B = 25 °$ ，则 $∠ B A C =$ $°$ ；
（2）如图②，延长 $A O$ 交 $⊙ O$ 于点 $D$ ，连接 $B D$ ，若 $A B = B D$ ，则 $∠ B A C =$ $°$ ；
（3）如图③，点 $E$ 是 $A O$ 上一点，且 $A E = A B$ ，连接 $B E$ 并延长交 $⊙ O$ 于点 $D$ ，连接 $O D$ ，若 $∠ B D O = 20 °$ ，则 $∠ B A C =$ $°$ ．

查看解析
11、某种麦粒在相同条件下进行发芽试验，结果如下表所示，则任取一粒麦粒，估计它能发芽的概率约为．（结果精确到 $0.01$ ）
试验的麦粒数 $n$
$100$
$200$
$500$
$1000$
$2000$
$5000$
发芽的麦粒数 $m$
$93$
$188$
$473$
$954$
$1906$
$4748$
发芽的频率 $\frac{m}{n}$
$0.93$
$0.94$
$0.946$
$0.954$
$0.953$
$0.9496$

查看解析
12、已知锐角 $△ A B C$ 中，O是 $A B$ 的中点，小明、小英二人想在 $A C$ 线段上找一点P，使得 $∠ A P B$ 为直角，其作法如图．对于小明、小英二人的作法，正确的是（）
小明的作法
过点B作与 $A C$ 垂直的直线，交 $A C$ 于点P，则P即为所求
小英的作法
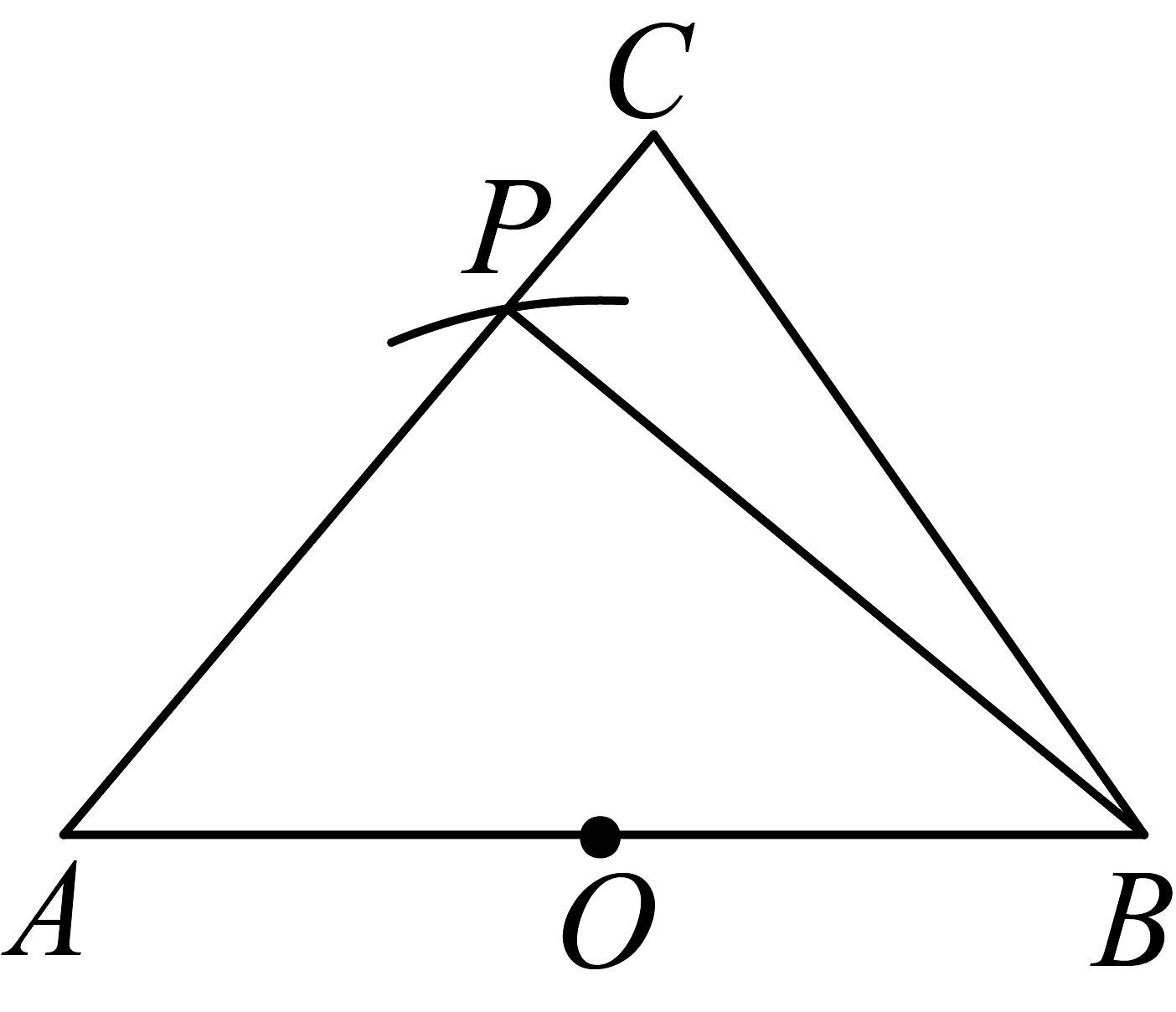
以O为圆心， $O A$ 长为半径画弧，交 $A C$ 于点P，则P即为所求

A、只有小明正确 B、只有小英正确 C、两人都正确 D、两人都不正确

查看解析
13、如图， $△ A B C$ 中， $∠ A C B = 90 ° ， A C = 3$ ．将 $△ A B C$ 绕点B逆时针旋转得到 $△ A^{'} B C^{'}$ ，点C的对应点 $C^{'}$ 落在 $A B$ 边上， $A^{'} B ＝ 5$ ，连接 $A A^{'}$ ．则 $A A^{'}$ 长为（　　）

A、 $2 \sqrt{2}$ B、 $\sqrt{10}$ C、3 D、4

查看解析
14、全班共有 $53$ 名学生，其中有 $26$ 名女生， $27$ 位男生，班级需选出一名女生参加升旗仪式，在女生中选到王芳的概率为（）

A、 $\frac{26}{53}$ B、 $\frac{27}{53}$ C、 $\frac{1}{27}$ D、 $\frac{1}{26}$

查看解析
15、关于x的方程 $x^{2} - 2 x - k = 0$ 有实数根，则k的取值范围是（　　）

A、 $k > - 1$ B、 $k \geq - 1$ C、 $k < - 1$ D、 $k \leq - 1$

查看解析
16、下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看解析
17、【定义概念】
如图，已知 $∠ A O B$ ，在 $∠ A O B$ 内部画射线 $O C$ ，得到三个角，分别为 $∠ A O C$ ， $∠ B O C$ ， $∠ A O B$ ，若这三个角中有一个角是另外一个角的2倍，则称射线 $O C$ 为 $∠ A O B$ 的“幸运线”，例如：图中 $∠ B O C = 2 ∠ A O C$ ，射线 $O C$ 为 $∠ A O B$ 的一条“幸运线”．（本题中所研究的角都是大于 $0 °$ 且小于 $180 °$ 的角．）
[阅读理解]
（1）一个角的平分线______这个角的“幸运线”．（填“是”或“不是”）
[初步应用]
（2）若 $∠ A O B = 45 °$ ，射线 $O C$ 为 $∠ A O B$ 的“幸运线”，求 $∠ A O C$ 的度数；
【解决问题】
（3）如图，已知 $∠ A O B = 60 °$ ，射线 $O M$ 从 $O A$ 出发，以每秒 $20 °$ 的速度绕点O逆时针旋转，同时，射线 $O N$ 从 $O B$ 出发，以每秒 $15 °$ 的速度绕点O逆时针旋转，设运动的时间为x秒（ $0 < t < 9$ ），若 $O M$ ， $O N$ ， $O A$ 三条射线中，一条射线恰好是以另外两条射线为边的角的“幸运线”，直接写出所有t的值．

查看解析
18、某体育用品商店推出促销活动，向客户提供了两种优惠方案：
方案一：买一件运动外套送一件卫衣；
方案二：运动外套和卫衣均在定价的基础上打 $8$ 折．
运动外套每件定价 $300$ 元，卫衣每件定价 $100$ 元 $.$ 在开展促销活动期间，某学校要到该商场购买运动外套 $100$ 件，卫衣 $x$ 件 $(x > 100)$ ．

(1)、用含 $x$ 的代数式表示；
方案一需付款______元；
方案二需付款______元 $.$

(2)、若该校购买卫衣 $150$ 件，以上两种方案哪种更合算？请通过计算说明理由．

查看解析
19、点A，B在数轴上的位置如图所示，点O为原点，且 $O A = 2$ ， $A B = 6$ ．

(1)、直接写出点A和点B表示的数；

(2)、若点C从点B出发以每秒3个单位长度的速度沿数轴向右运动，求4秒后点C表示的数；

(3)、对折纸面，使数轴上点A与点B重合，直接写出与（2）中4秒后的点C重合的点所表示的数．

查看解析
20、如图，有A、B、C、D四个点．使用直尺、圆规按下列要求画出图形（不写作法，保留作图痕迹）．

(1)、画线段 $A B$ ，射线 $A D$ ，直线 $A C$ ；

(2)、连接 $B D$ ， $B D$ 与直线 $A C$ 交于点E；

(3)、在线段 $A B$ 上，截取 $A F = A D$ ．

查看解析

上一页 1083 1084 1085 1086 1087 下一页跳转

试验的麦粒数 $n$	$100$	$200$	$500$	$1000$	$2000$	$5000$
发芽的麦粒数 $m$	$93$	$188$	$473$	$954$	$1906$	$4748$
发芽的频率 $\frac{m}{n}$	$0.93$	$0.94$	$0.946$	$0.954$	$0.953$	$0.9496$