相关试卷

1、如图，在数轴上点A，B，C分别表示的数为a，b，c．已知a，b分别是多项式 $- x^{3} y^{2} - 2$ 的次数和常数项，c是单项式 $- 6 x y^{2}$ 的系数．

(1)、填空： $a =$ ______， $b =$ ______， $c =$ ______；并在数轴上标出原点O；

(2)、若动点M，N分别从点A，B同时出发沿数轴向左运动，点M的速度是每秒2个单位长度，点N的速度是每秒1个单位长度，求运动几秒后，点M可以追上点N？

(3)、若动点P从原点O出发，以每秒3个单位长度的速度向左运动，同时另一动点Q从点A出发，以每秒2个单位长度的速度向左运动，到达原点后立即以原来的速度返回，向右运动．设运动的时间为t秒，当点Q到原点O的距离为3时，求点P表示的数．

查看解析
2、已知 $(2 x^{2} + a x - y + b) - (2 b x^{2} - 3 x + 5 y - 1)$ 的值与字母x的取值无关，求代数式 $6 (a^{2} - a b - b^{2}) - 2 (3 a^{2} + a b - 3 b^{2})$ 的值．

查看解析
3、星光中学召开秋季运动会，七（1）班同学准备统一购买运动鞋和运动服．已知 $A$ ， $B$ 两家运动品牌店的一款运动鞋每双 $120$ 元，运动服每套 $300$ 元．国庆期间，这两家店都开展促销活动，如下：
A店：买 $2$ 套运动服送一双运动鞋；
B店：运动服原价，运动鞋打六五折．
若七（1）班要购买运动服 $20$ 套，运动鞋 $x$ 双（ $x$ 大于 $10$ ）．

(1)、分别求出七（1）班在 $A$ 店， $B$ 店购买时，所要付款的金额；（用含 $x$ 的代数式表示）

(2)、当 $x = 25$ 时，请你通过计算说明到哪家店购买更划算？

查看解析
4、外卖送餐为我们生活带来了很多便利，小宇所在的兴趣小组调查了外卖员小李一周的送餐情况．若规定每天送餐量 $50$ 单为标准，超过标准的单数记为“ $+$ ”，少于标准的单数记为“ $-$ ”，下表是外卖员小李一周的送餐量情况．（送一次外卖称为一单）
星期
一
二
三
四
五
六
日
送餐量
$- 5$
$+ 6$
$- 3$
$+ 12$
$- 7$
$+ 8$
$+ 13$

(1)、小李这一周送餐量最多一天比最少一天多送多少单？

(2)、小李这一周共送餐多少单？

(3)、小李每天的工资构成：底薪 $50$ 元 $+$ 送单补贴．送单补贴方案：每天送餐量不超过 $50$ 单的部分，每单补贴 $2.5$ 元；超过 $50$ 单但不超过 $60$ 单的部分，每单补贴 $3.5$ 元；超过 $60$ 单的部分，每单补贴 $5$ 元．求小李这一周的工资总额．

查看解析
5、有理数a，b，c在数轴上的位置如图所示，化简： $|b - c| + |a + b| - |a - c|$ ．

查看解析
6、计算：

(1)、 $(- 3) - (- 5) - (+ 7) + (+ 4)$

(2)、 $- 2^{4} + (1 - \frac{1}{3}) \times |3 - {(- 3)}^{2}|$

查看解析
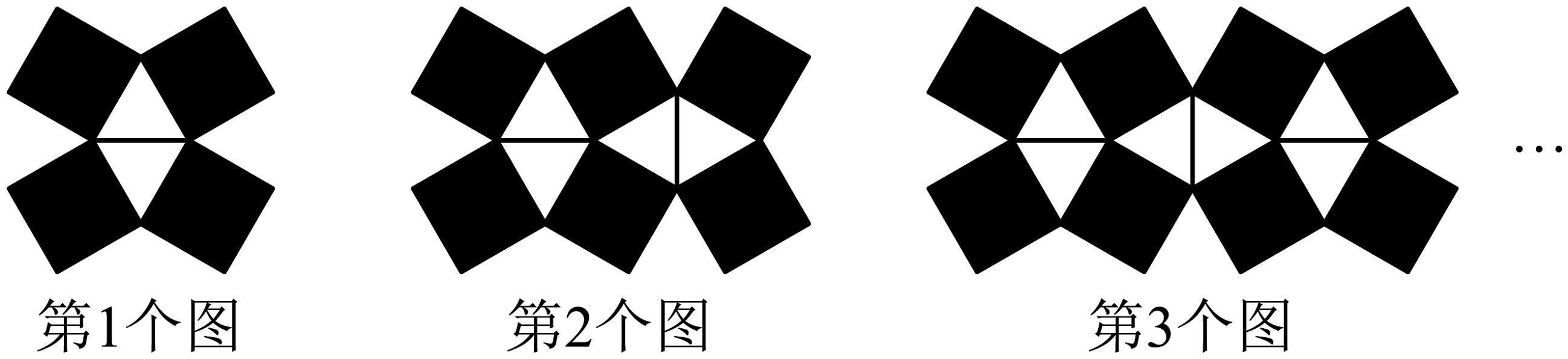
7、如图，下列图形都是由同样大小的正方形按一定的规律组成的，其中第 $1$ 个图形有 $4$ 个正方形，第 $2$ 个图形有 $6$ 个正方形，第 $3$ 个图形有 $8$ 个正方形，…，依此规律，第 $n$ 个图形中有个正方形．（用含 $n$ 的代数式表示）

查看解析
8、如图所示的数轴上，点 $O$ 表示原点，点 $A$ 表示的数是 $3$ ，若点 $B$ 距离点 $A$ 是 $5$ 个单位长度，则点 $B$ 表示的数是（）

A、 $5$ B、 $5$ 或 $- 3$ C、 $8$ 或 $- 2$ D、 $8$ 或 $- 5$

查看解析
9、如图是小宇设计的一个求代数式值的运算程序框图，若开始输入的x值为 $- 3$ ，则最后输出的结果是（）

A、 $- 7$ B、 $- 17$ C、 $- 28$ D、 $- 23$

查看解析
10、下列说法中，不正确的是（）

A、 $- x + 1$ 不是单项式 B、多项式 $3 x^{2} - x y - 4$ 的次数是 $4$ C、单项式 $- 2 x^{2}$ 的系数是 $- 2$ D、多项式 $x - 5$ 的常数项是 $- 5$

查看解析
11、若 $|a - 4| = |a| + |- 4|$ ，则a的值是（）

A、任意有理数 B、任意一个非负数 C、任意一个非正数 D、任意一个负数

查看解析
12、下列各组数中，互为倒数的一组是（　　）

A、4和 $- 4$ B、 $- 2$ 和 $- \frac{1}{2}$ C、 $- 3$ 和 $\frac{1}{3}$ D、0和0

查看解析
13、广安市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米售价a元，其中 $∠ A B C = 150 °$ ，则购买这种草皮至少需要多少元．

查看解析
14、小马虎同学在计算一个多项式A乘 $(1 - 2 x)$ 时，因抄错运算符号，算成了加上 $(1 - 2 x)$ ，得到的结果是 $x^{2} - x + 1$ ．

(1)、这个多项式A是多少？

(2)、正确的计算结果是多少？

查看解析
15、中国古代在数学方面的成就辉煌，《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》等都是我国古代数学的重要文献．某数学兴趣小组准备采用抽签的方式确定学习内容，将书目制成编号为 $A$ ， $B$ ， $C$ ， $D$ 的4张卡片（卡片除编号和书目外，其余完全相同)，现将这4张卡片背面朝上洗匀放好．

(1)、若从4张卡片中随机抽取一张，则抽到《九章算术》的概率为_____________；

(2)、若从4张卡片中随机抽取两张，求抽到《九章算术》和《海岛算经》的概率．（请用“画树状图”或“列表”等方法写出分析过程）

查看解析
16、如图，矩形 $A B C D$ 的对角线 $A C ， B D$ 相交于点O，若 $O A = A B$ ，则 $∠ B O C$ 的度数为（）

A、 $60 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看解析
17、已知代数式 $A = 2 x^{2} + 3 x y + 2 y$ ， $B = x^{2} - x y + x$ ．

(1)、求 $A - 2 B$ ；

(2)、当 $x = - 1$ ， $y = 3$ 时，求 $A - 2 B$ 的值；

(3)、若 $A - 2 B$ 的值与 $x$ 的取值无关，求 $y$ 的值．

查看解析
18、已知如图，点 C 是线段 AB 的黄金分割点（AC＞BC），则下列结论中正确的是（）

A、AB²＝AC²+BC² B、BC²＝AC•BA C、 $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{A C}{B C} = \frac{\sqrt{5} - 1}{2}$

查看解析
19、阅读下面材料：点A、B在数轴上分别表示有理数a、b，在数轴上A、B两点之间的距离 $A B = |a - b|$ ．回答下列问题：

(1)、数轴上表示 $- 3$ 和1两点之间的距离是____，数轴上表示x和2的两点之间的距离是____；

(2)、数轴上表示a和1的两点之间的距离为6，则a表示的数为____；

(3)、若x表示一个有理数，则 $|x + 2| + |x - 4|$ 有最小值吗？若有，请求出最小值；若没有，请说明理由．

查看解析
20、中国是最早采用正负数表示相反意义的量的国家，如果将“向东走 $50$ 米”记作“ $+ 50$ 米”，那么“向西走 $80$ 米”记作（）

A、 $- 80$ 米 B、 $+ 80$ 米 C、 $+ 30$ 米 D、 $- 30$ 米

查看解析

上一页 1086 1087 1088 1089 1090 下一页跳转

星期	一	二	三	四	五	六	日
送餐量	$- 5$	$+ 6$	$- 3$	$+ 12$	$- 7$	$+ 8$	$+ 13$