相关试卷

1、为筹备学校秋季运动会，小明制作了如图所示的宣传牌，在正五边形 $A B C D E$ 和正方形 $C D F G$ 中， $C F$ ， $D G$ 的延长线分别交 $A E$ ， $A B$ 于点M，N，则 $∠ F M E$ 的度数是°．

查看解析
2、如图，将长为 $8 cm$ 的铁丝首尾相接围成半径为 $2 cm$ 的扇形．则 $S_{扇形} =$ ${cm}^{2}$ ．

查看解析
3、如图，已知A，B，C是 $⊙ O$ 上三点， $∠ C = 20 °$ ，则 $∠ A O B$ 的度数为．

查看解析
4、如图．在平面直角坐标系中，四边形 $A B O C$ 是正方形，点A的坐标为 $(1, 1)$ ，弧 $A A_{1}$ 是以点B为圆心， $B A$ 为半径的圆弧；弧 $A_{1} A_{2}$ 是以点O为圆心， $O A_{1}$ 为半径的圆弧；弧 $A_{2} A_{3}$ 是以点C为圆心， $C A_{2}$ 为半径的圆弧；弧 $A_{3} A_{4}$ 是以点A为圆心， $A A_{3}$ 为半径的圆弧．继续以点B，O，C，A为圆心按上述作法得到的曲线 $A A_{1} A_{2} A_{3} A_{4} A_{5}$ …称为正方形的“渐开线”，则点 $A_{2024}$ 的坐标是（）

A、 $(1, 2025)$ B、 $(1, 2024)$ C、 $(2025, 0)$ D、 $(2024, 0)$

查看解析
5、数学期中考试，齐思所在班级的平均分是112分，苗想所在班级的平均分是122分，这次齐思的数学成绩与苗想相比（）

A、齐思分数高 B、苗想分数高 C、他们分数一样 D、以上三种都有可能

查看解析
6、如图， $O$ 是弧 $A D$ 所在圆的圆心．已知点B、C将弧AD三等分，那么下列四个选项中不正确的是（）

A、 $\overset{⌢}{A C} = 2 \overset{⌢}{C D}$ B、 $A C = 2 C D$ C、 $∠ A O C = 2 ∠ C O D$ D、 $S_{扇形 A O C} = 2 S_{扇形 C O D}$ ．

查看解析
7、下列说法：①三点确定一个圆；②圆的直径是圆的对称轴；③三角形的外心到三个顶点的距离相等．其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看解析
8、若 $⊙ O$ 的半径为 $6 cm$ ， $P O = 5 cm$ ，则点P与 $⊙ O$ 的位置关系是（）

A、点P在 $⊙ O$ 外 B、点P在 $⊙ O$ 上 C、点P在 $⊙ O$ 内 D、点P在 $⊙ O$ 内或 $⊙ O$ 上

查看解析
9、老师出示问题：“解方程 $x^{2} - 1 = 0$ ， ”四位同学给出了以下答案：
甲 $x = 1$ ；乙 $x_{1} = x_{2} = 1$ ；丙 $x_{1} = x_{2} = - 1$ ；丁 $x_{1} = 1$ ， $x_{2} = - 1$ ．
下列判断正确的是（）

A、甲正确 B、乙正确 C、丙正确 D、丁正确

查看解析
10、已知 $α$ 、 $β$ 是关于x的一元二次方程 $x^{2} + (2 m + 3) x + m^{2} = 0$ 的两个不相等的实数根

(1)、直接写出m的取值范围

(2)、若满足 $\frac{1}{α} + \frac{1}{β} = - 1$ ，求m的值．

查看解析
11、某乳品公司向某地运输一批牛奶，由铁路运输每千克只需运费0.58元；由公路运输，每千克需运费0.28元，运完这批牛奶还需其他费用600元．
（1）设该公司运输的这批牛奶为 $x kg$ ，选择铁路运输时，所需运费为 $y_{1}$ 元，选择公路运输时，所需运费为 $y_{2}$ 元，请分别写出 $y_{1}$ ， $y_{2}$ 与x之间的关系式；
（2）若公司只支出运费 $1500$ 元，则选用哪种运输方式运送的牛奶多？若公司运送 $1500 kg$ 牛奶，则选用哪种运输方式所需费用较少？

查看解析
12、如图，在直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (1, 4)$ ， $B (4, 2)$ ， $C (3, 5)$ ，请回答下列问题．

(1)、作 $△ A B C$ 的关于y轴的对称图形，A、B、C对应点坐标分别为 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ ．

(2)、分别写出 $△ A^{'} B^{'} C^{'}$ 的坐标： $A^{'}$ _______； $B^{'}$ ______； $C^{'}$ _____；

查看解析
13、已知实数 $a, b, c$ 在数轴上的位置如图所示，化简代数式 $\sqrt{{(a - c)}^{2}} - \sqrt{{(c - b)}^{2}}$ 的结果等于．

查看解析
14、若 $△ A B C$ 为等腰三角形，其中b，c满足 $|c - 5| + \sqrt{b - 2} = 0$ ，则 $△ A B C$ 的周长为（）

A、9 B、 $10$ C、9或 $12$ D、 $12$

查看解析
15、如图所示的一段楼梯，高 $B C$ 是3米，斜边 $A B$ 长是5米，现打算在楼梯上铺地毯，至少需要地毯的长度为（）

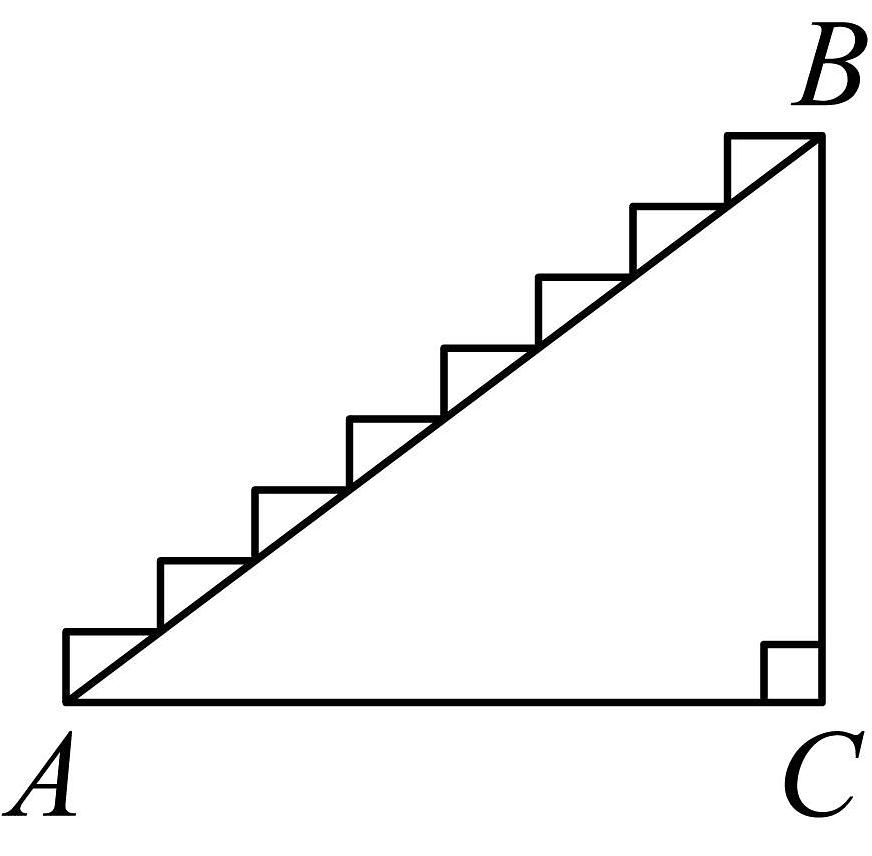A、4米 B、5米 C、6米 D、7米

查看解析
16、下列式子中，为最简二次根式的是（　　）

A、 $\sqrt{30}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\sqrt{a^{2}}$

查看解析
17、“疫情防控，我们在一起”，每个人都是疫情防控的重要一环，下面是人民日报发布的疫情防控宣传图，上有图案和文字说明，其中图案是轴对称图形的是（）

A、有症状早就医 B、防控疫情我们在一起 C、打喷嚏捂口鼻 D、勤洗手勤通风

查看解析
18、下列各数中，最大的数是（）

A、1 B、0 C、 $- 2$ D、 $\sqrt{2}$

查看解析
19、华罗庚先生说：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休”．
【知识储备】：数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．点 $M$ ， $N$ 在数轴上分别表示有理数 $m$ ， $n$ ，则 $M$ ， $N$ 两点之间的距离可表示为 $| m - n |$ ．
例如：从“形”的角度看： $|3 - 1|$ 可以理解为数轴上表示 $3$ 和 $1$ 的两点之间的距离； $|3 + 1|$ 可以理解为数轴上表示 $3$ 与 $- 1$ 的两点之间的距离．从“数”的角度看：数轴上表示 $4$ 和 $- 3$ 的两点之间的距离可用 $|4 - (- 3)|$ 表示．根据以上阅读材料探索下列问题
【初步运用】
（1）①数轴上表示 $- 2$ 和 $5$ 两点之间的距离是               ；
②数轴上表示 $x$ 与 $3$ 两点间的距离是             ；
（2）下面对式子 $| x + 1 | + | x - 3 |$ 进行探究：
①当表示数x的点在 $- 1$ 与3之间移动时， $| x + 1 | + | x - 3 |$ 的值总是一个固定的值为：             ．
②如果表示数 $x$ 和 $- 1$ 的两点之间的距离是 $4$ ，那么 $x =$               ．
③使 $| x + 1 | + | x - 3 | = 8$ ，数轴上表示的数 $x =$       ．
【深入探究】
（3）利用数轴解决问题：
①找出所有符合条件的整数点 $x$ ，使得 $|x + 3 |+| x - 4| = 7$ ，这些点表示的数的和是           ．
②利用数轴解决问题：当 $x =$         时， $|x + 3 |+| x - 1 |+| x - 4|$ 的值最小，最小值是         ．

查看解析
20、观察下面的变形规律：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$
$\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$
$\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4} \cdot \cdot \cdot \cdot \cdot \cdot$
解答下面的问题：

(1)、根据上述变化规律写出下面等号后面的式子：
$\frac{1}{4 \times 5} =$ ； $\frac{1}{2024 \times 2025} =$ ．
若 $n$ 为正整数，猜想 $\frac{1}{n (n + 1)} =$ ．

(2)、求值 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2024 \times 2025}$ ．

查看解析

上一页 1076 1077 1078 1079 1080 下一页跳转