-
1、甲、乙、丙、丁四位同学参加校田径运动会4×100米接力跑比赛,因为丁的速度最快,所以由他负责跑最后一棒,其他三位同学的跑步顺序随机安排.
(1)请用画树状图或列表的方法表示甲、乙、丙三位同学所有的跑步顺序;
(2)请求出正好由丙将接力棒交给丁的概率.
-
2、如图,中, .
 (1)、作的角平分线交于点(要求:用尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,若 , , 求的长.
(1)、作的角平分线交于点(要求:用尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,若 , , 求的长. -
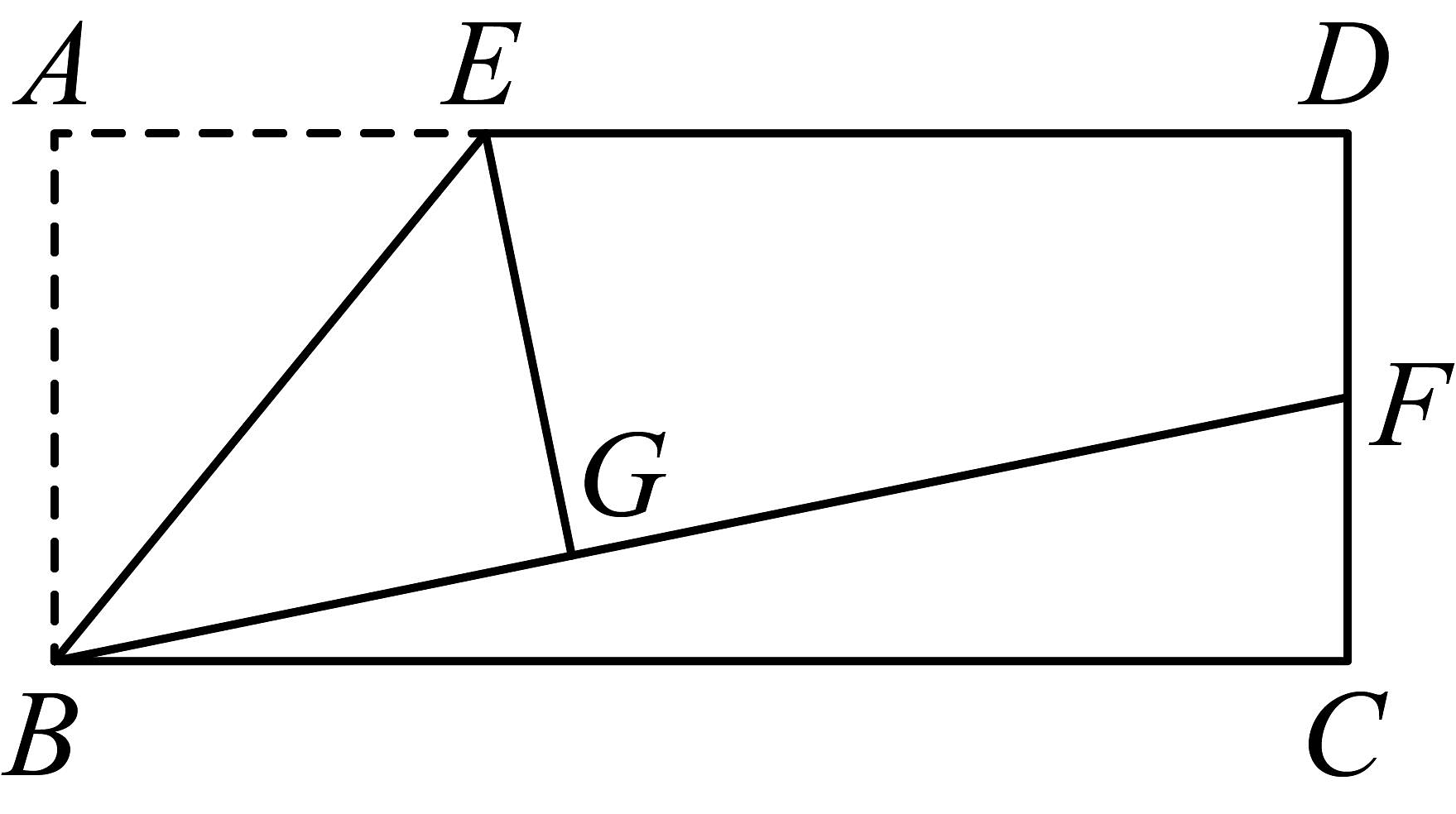
3、如图,矩形ABCD中,AE=AD,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=FD=3,则BC的长为 .
-
4、如图,坡面CD的坡比为 , 坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=米,则小树AB的高是 .

-
5、如图,在正方形中,对角线相交于点 , 点在边上,且 , 连接交于点 , 过点作 , 连接并延长,交于点 , 过点作分别交于点 , 交的延长线于点 , 现给出下列结论:①;②;③;④;其中正确的结论有( )
 A、①②③ B、②③④ C、①②④ D、①②③④
A、①②③ B、②③④ C、①②④ D、①②③④ -
6、如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB与CD相交于点P,则tan∠APD的值为( )
 A、2 B、 C、3 D、
A、2 B、 C、3 D、 -
7、如图,已知点A是反比例函数的图像上一点,AB∥x轴交另一个反比例函数的图像于点B,C为x轴上一点,若S△ABC=2,则k的值为( )
 A、4 B、2 C、3 D、1
A、4 B、2 C、3 D、1 -
8、若点A(﹣6,y1),B(﹣2,y2),C(3,y3)在反比例函数(a为常数)的图象上,则y1 , y2 , y3大小关系为( )A、y1>y2>y3 B、y2>y3>y1 C、y3>y2>y1 D、y3>y1>y2
-
9、一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最少是( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
10、已知两个完全相同的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为 .

-
11、已知二次函数(b,c为常数)的图象经过点 , 对称轴为直线 .(1)、求二次函数的表达式;(2)、若点向上平移2个单位长度,向左平移m()个单位长度后,恰好落在的图象上,求m的值;
-
12、已知a是方程的一个根,则代数式的值是 .
-
13、【阅读理解】若 , , 求的值.
解:因为 , 所以 , 即: , 又因为 , 所以
【方法应用】
(1)若 , , 求的值.
(2)若 , 则________.
【拓展提升】
(3)在中, , , 的面积为 , 求的长.
(4)如图,在四边形中,对角线于点O,且 , , 则四边形的面积为_________.

-
14、立德朝阳中学的小花,准备假期和父母出去旅游,于是在网上购买了一个行旅拉杆箱,如图 , 图分别是拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆、箱长、拉杆的长度都相等,即 , 点在线段上,点在上,支杆 .
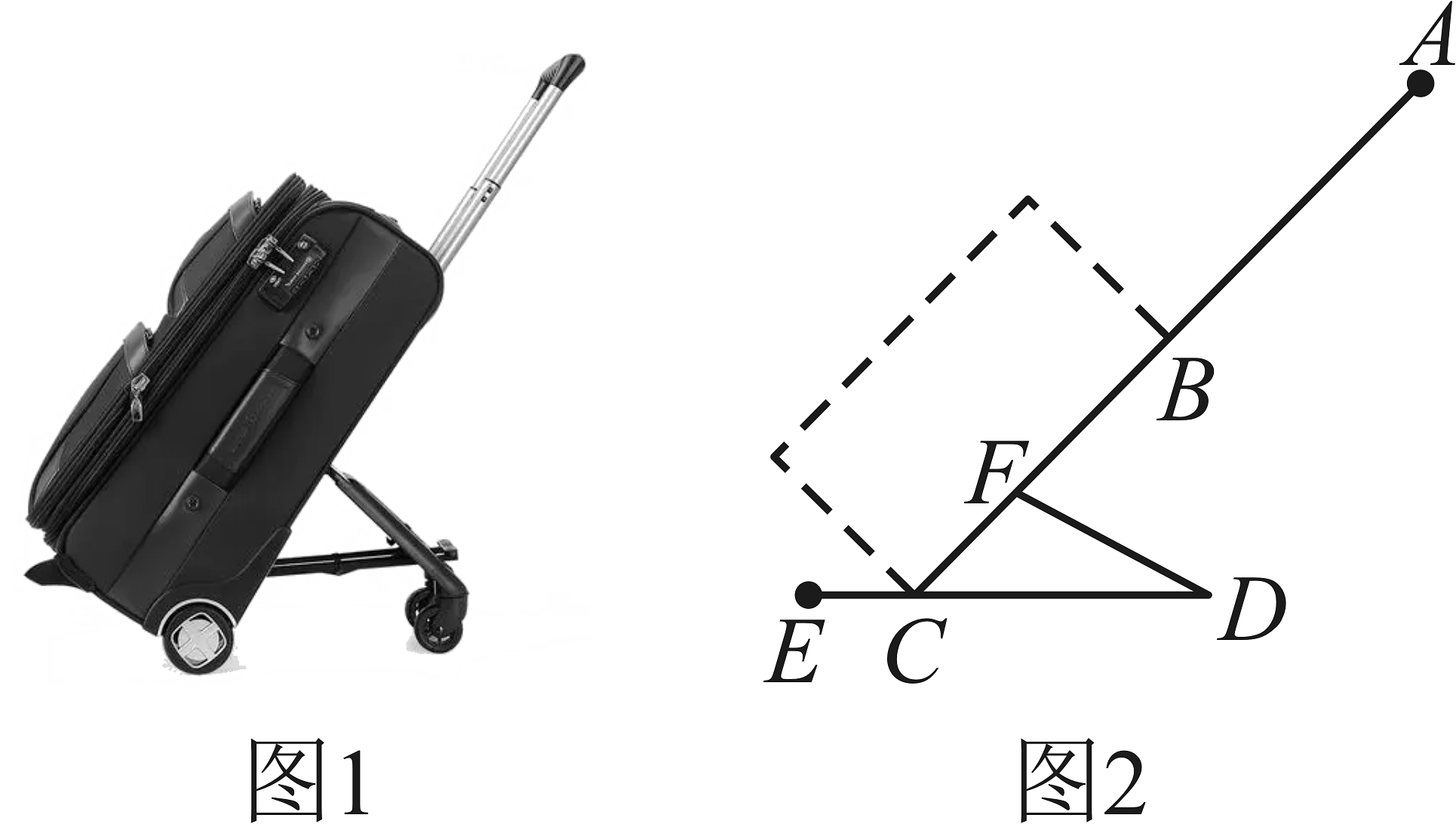 (1)、当与点重合,时,是什么三角形.(2)、当时,求的长.
(1)、当与点重合,时,是什么三角形.(2)、当时,求的长. -
15、如图,在四边形中, , , , , .
 (1)、求的长;(2)、求四边形的面积.
(1)、求的长;(2)、求四边形的面积. -
16、计算:
-
17、如图, 中, , , , 在数轴上,以点为圆心,的长为半径作弧交数轴的正半轴于 . 若点在数轴上表示的数为 , 则点表示的数为 .

-
18、在等腰三角形中, , , 则边上的高是 .
-
19、若电影院的5排2号记为 , 则3排5号记为 .
-
20、下列说法中,不正确的是( )A、的绝对值是 B、的平方根是 C、的算术平方根是1 D、的立方根是1