-
1、先化简,再求值: , 其中 , .
-
2、抛物线的顶点坐标为( )A、 B、 C、 D、
-
3、如图,四个全等的直角三角形拼成“赵爽弦图”,其中四边形与四边形都是正方形.连结并延长,交于点P,点P为的中点.若 , , 则正方形的面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、在一个三角形中,如果一个角是另一个角的2倍,这样的三角形我们称之为“倍角三角形”.如图,在中, , , 点P是线段上一点(不与A,B重合),连接 .
 (1)、若 , 则 “倍角三角形”(填“是”或“不是”);(2)、若是“倍角三角形”,求的度数.
(1)、若 , 则 “倍角三角形”(填“是”或“不是”);(2)、若是“倍角三角形”,求的度数. -
5、如图, , , 点E、F在上,且 . 求证: .

-
6、如图,点P是内任意一点, , 点M和点N分别是射线和射线上的动点.若周长的最小值是 , 求的度数.

-
7、如图,已知点与坐标系原点重合,若点P在x轴上,且是等腰三角形,则点P的坐标最多有( )个.
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
8、如图,直线分别与x轴、y轴相交于点E和点F,点E的坐标为 , 点A的坐标为 .
 (1)、求k的值;(2)、若点是第二象限内的直线上的一个动点,在点P运动过程中,试写出的面积S与x的函数关系式,并写出自变量x的取值范围;(3)、在(2)条件下,探究:当P运动到什么位置时,的面积为4,并说明理由.
(1)、求k的值;(2)、若点是第二象限内的直线上的一个动点,在点P运动过程中,试写出的面积S与x的函数关系式,并写出自变量x的取值范围;(3)、在(2)条件下,探究:当P运动到什么位置时,的面积为4,并说明理由. -
9、①,
以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:
②.
(1)、请用不同的方法化简,参照①式得= ;参照②式得= ;(2)、化简 . -
10、某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
 (1)、分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式.(2)、两种租书方式每天租书的收费分别是多少元?
(1)、分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式.(2)、两种租书方式每天租书的收费分别是多少元? -
11、中, ,过A作 , 垂足为H,求的长.

-
12、已知点 , 请分别根据下列条件,求出点P的坐标.(1)、点Q的坐标是 , 轴;(2)、点P在第一、三象限的角平分线上.
-
13、如图,在中,于点D,求的长.

-
14、在平面直角坐标系中,作出 , 使各顶点的坐标分别是: , , , 并求出的面积.

-
15、计算
-
16、在平面直角坐标系中,有一个微型机器人从原点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示:

则点的坐标是 .
-
17、直线平行于直线 , 且过点 , 则直线的函数解析式是 .
-
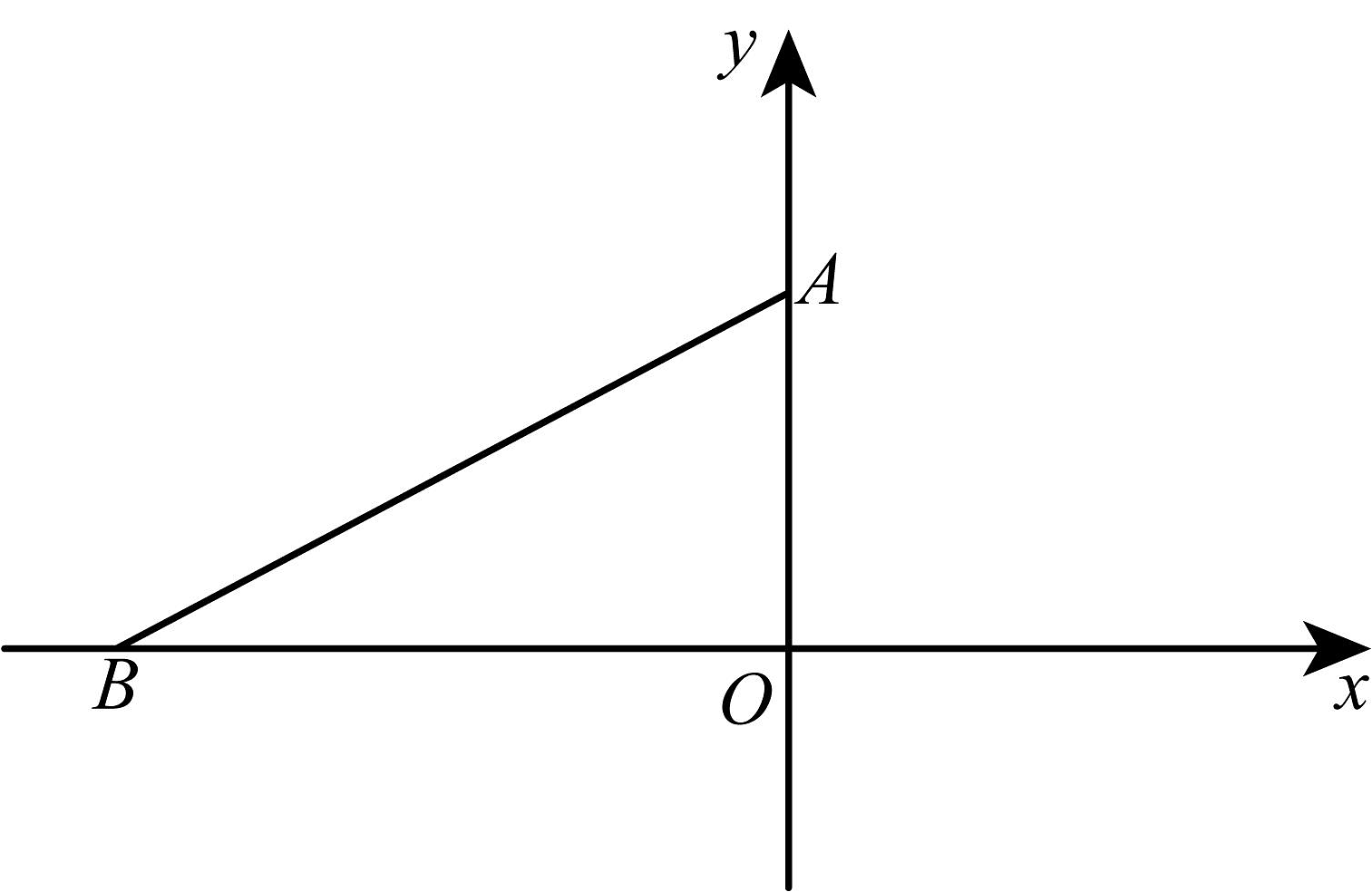
18、如图,点到原点的距离为 .

-
19、点在直角坐标系的轴上,则点的坐标为 .
-
20、若一个正数的平方根是和 , 则 .