相关试卷

1、已知 $∠ A O B = 130 °$ ，作射线 $O C$ ， $∠ B O C = α$ ，射线 $O D$ ， $O E$ 分别是 $∠ A O B, ∠ B O C$ 的平分线．

(1)、当射线 $O C$ 在 $∠ A O B$ 的内部时，如图，若 $α = 30 °$ ，求 $∠ D O E$ 的度数；
下面是小东的解答过程，请你补充完整．
解：（1）因为 $O D$ 是 $∠ A O B$ 的平分线，且 $∠ A O B = 130 °$ ，
所以 $∠ B O D = \frac{1}{2} ∠ A O B = 65 °$ （______）（填写推理依据）．
因为 $O E$ 是 $∠ B O C$ 的平分线，且 $∠ B O C = α = 30 °$ ，
所以 $∠ B O E = \frac{1}{2} ∠ B O C =$ ______，
所以 $∠ D O E = ∠ B O D - ∠ B O E =$ ______．

(2)、当射线 $O C$ 在 $∠ A O B$ 的外部时， $∠ D O E$ 的度数为______．（用含 $α$ 的式子表示）

查看解析
2、如图，已知线段 $A B$ 和点 $C$ ，已知点 $D$ 是线段 $A B$ 的中点．

根据要求画图，并填空：

(1)、画直线 $D C$ ；

(2)、画射线 $B C$ ；

(3)、连接 $A C$ 并延长到点 $E$ ，使 $C E = A C$ ；（用尺规作出线段 $C E$ ，要求保留作图痕迹）

(4)、连接 $B E$ ，探究并猜想线段 $D C$ ， $B E$ 之间具有怎样的等量关系？写出你的猜想无需说明理由：______；

(5)、在 $B C$ 上确定一点 $P$ ，使线段 $P E$ 与线段 $P D$ 的和最短，保留作图痕迹并说明画图的依据是：______．

查看解析
3、解下列方程：

(1)、 $5 x - 3 (x - 1) = 6$ ；

(2)、 $\frac{5 x - 1}{4} = \frac{3 x + 1}{2} - \frac{2 - x}{3}$ ；

(3)、 $\frac{x - 2}{4} = 1 - \frac{2 x - 1}{3}$ ．

查看解析
4、先化简，再求值： $3 x^{2} - 2 (x^{2} - \frac{1}{3} y^{2}) + \frac{1}{3} y^{2}$ ，其中 $x = - 1$ ， $y = \frac{2}{3}$ .

查看解析
5、计算题：

(1)、 $3 \frac{1}{2} \times (- \frac{6}{7}) + (- 10) \div (- \frac{2}{3})$ ；

(2)、 $- 1^{4} + {(- 2)}^{3} \div 4 \times [5 - {(- 3)}^{2}]$ ．

查看解析
6、“霜降见霜，谷米满仓”，2023年我国粮食再获丰收．据统计，去年秋粮的种植面积为13.1亿亩，比前年增加了700多万亩，奠定了增产的基础．将1310000000用科学记数法表示应为．

查看解析
7、在体育课的立定跳远测试中，以 $2.00 m$ 为标准，若小明跳出了 $2.35 m$ ，可记作 $+ 0.35 m$ ，则小亮跳出了 $1.65 m$ ，应记作 $m$ ．

查看解析
8、某商店在甲批发市场以每包 $m$ 元的价格进了 $60$ 包茶叶，又在乙批发市场以每包 $n$ 元 $(m < n)$ 的价格进了同样的 $40$ 包茶叶，如果商家以每包 $\frac{m + n}{2}$ 元的价格卖出这种茶叶，卖完后，这家商店的盈亏情况为（）

A、盈利 $10 (m - n)$ 元 B、亏损 $10 (n - m)$ 元 C、盈利 $10 (n - m)$ 元 D、没盈利也没亏损

查看解析
9、如图， $O$ 是线段 $A B$ 的中点， $P$ 是 $A O$ 上一点．已知 $B P$ 比 $A P$ 长 $6$ ，则 $O P =$ （）

A、6 B、2 C、 $\frac{3}{2}$ D、3

查看解析
10、综合与实践：
问题情境：已知 $O M$ 是 $∠ A O B$ 的平分线，P是射线 $O M$ 上的一点，点C，D分别在射线 $O A$ ， $O B$ 上，连接 $P C, P D$ ．

(1)、初步探究：如图1，当 $P C ⊥ O A$ ， $P D ⊥ O B$ 时， $P C$ 与 $P D$ 的数量关系是；

(2)、深入探究：如图2，点C，D分别在射线 $O A$ ， $O B$ 上运动，且 $∠ A O B = 90 °$ ，当 $∠ C P D = 90 °$ 时， $P C$ 与 $P D$ 在（1）中的数量关系还成立吗？请说明理由；

(3)、拓展应用：如图3，如果点C在射线 $O A$ 上运动，且 $∠ A O B = 90 °$ ，当 $∠ C P D = 90 °$ 时，点D落在了射线 $O B$ 的反向延长线上，若点P到 $O B$ 的距离为3， $O D = 1$ ，求 $O C$ 的长（直接写出答案）．

查看解析
11、（1）一个多边形的内角和是 $1080 °$ ，若该多边形每个内角都相等，求每一个外角的度数．
（2）如图， $∠ A = ∠ B$ ， $C E ∥ D A$ ， $∠ E C B = 60 °$ ，求证： $△ B C E$ 是等边三角形．

查看解析
12、已知：如图所示，在 $△ A B C$ 中，点 $D$ ， $E$ ， $F$ 分别为 $B C$ ， $A D$ ， $C E$ 的中点，且 $S_{△ A B C} = 4 {cm}^{2}$ ，则阴影部分的面积为 ${cm}^{2}$ ．

查看解析
13、如图，小明不小心将书上的一个三角形用墨迹污染了一部分，但他很快就根据所学知识画出了一个和书上完全一样的三角形，那么这两个三角形完全一样的依据为．

查看解析
14、如图所示，该正六边形图案的外角和为．

查看解析
15、如图，已知 $∠ A B C$ ，以点B为圆心，以任意长为半径作弧分别交射线 $B A, B C$ 于点M，N，分别以点M，N为圆心，大于 $\frac{1}{2}$ $M N$ 长为半径作弧，两弧相交于点P；在射线 $B C$ 上取点H，以点H为圆心，以线段 $B H$ 长为半径作弧交射线 $B P$ 于点D；点E，F分别在射线 $B A, H D$ 上， $∠ A E F = 68 °$ ，射线 $E F, B D$ 交于点G， $∠ F D G = 39 °$ ，则 $∠ E G B =$ （　　）

A、 $29 °$ B、 $30 °$ C、 $38 °$ D、 $39 °$

查看解析
16、如图，将矩形纸片 $A B C D$ 沿对角线 $B D$ 折叠一次，则图中全等三角形有（）

A、2对 B、3对 C、4对 D、5对

查看解析
17、如图， $△ A B C ≌ △ D B C$ ， $A C = 2$ ，则 $D C$ 等于（）

A、1 B、2 C、3 D、4

查看解析
18、甲骨文是我国古代的一种文字，反映了我国悠久的历史文化，下列甲骨文中，可看作是轴对称图形的是（）

A、 B、 C、 D、

查看解析
19、如图，矩形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，点 $E$ 与点 $O$ 关于 $C D$ 对称．

(1)、连接 $C E$ 、 $D E$ ，求证：四边形 $C E D O$ 是菱形；

(2)、若 $A B = 2$ ， $∠ A O B = 60 °$ ，求点 $E$ 、 $O$ 之间的距离．

查看解析
20、如图，一次函数 $y = - x + 3$ 的图象与 $x$ 轴、 $y$ 轴分别交于A、 $B$ 两点，二次函数 $y = - x^{2} + b x + c$ 的图象经过点A， $B$ ．

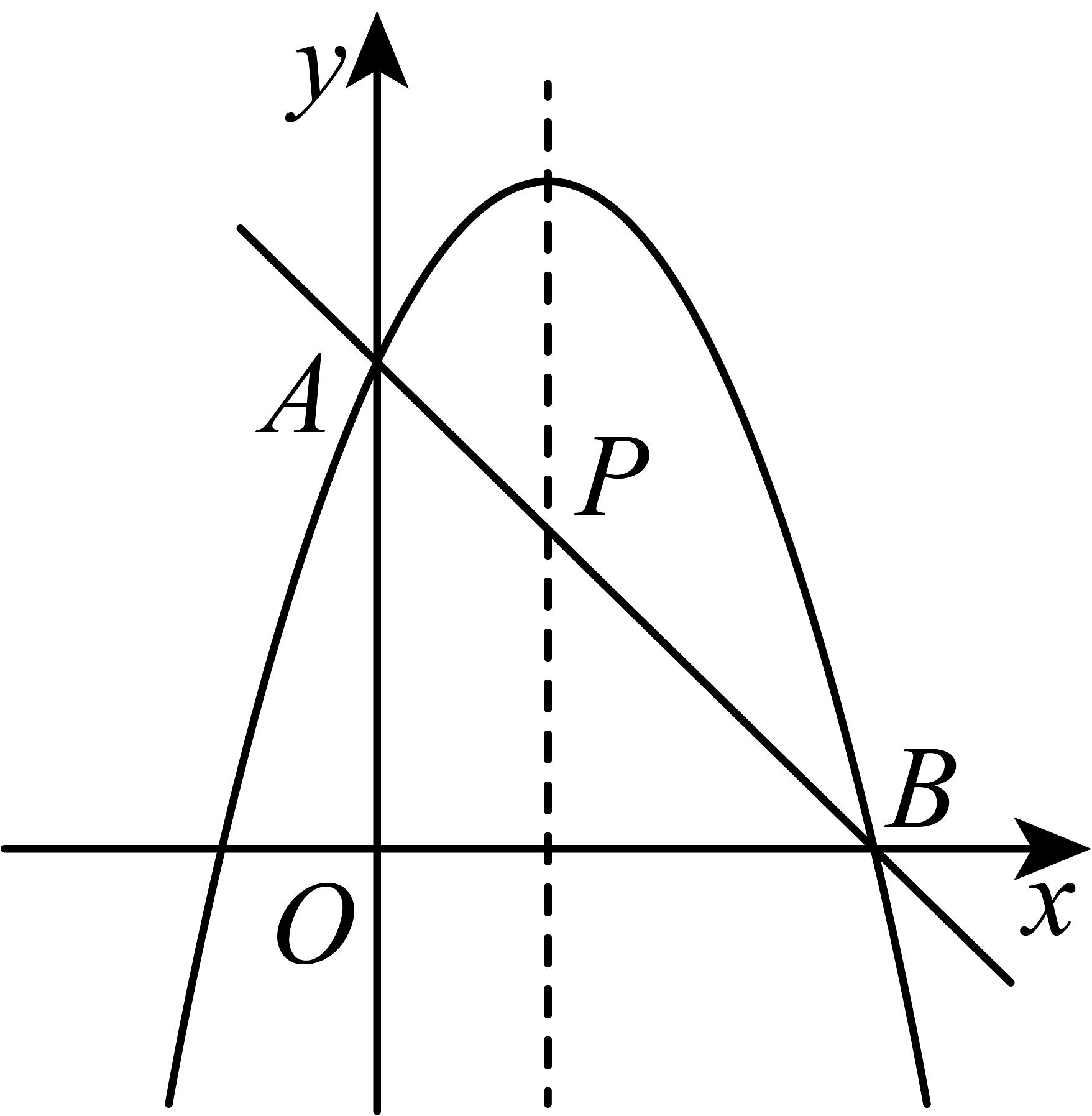(1)、求二次函数的表达式；

(2)、直线 $A B$ 与二次函数图象的对称轴交于点 $P$ ，求点 $P$ 坐标．

查看解析

上一页 999 1000 1001 1002 1003 下一页跳转