相关试卷
- 广东省部分学校2025-2026学年高三1月综合练习数学试卷
- 广东省广州第四中学2025-2026学年高三上学期期末数学试题
- 广东省深圳市龙岗区布吉高级中学2025-2026学年高二高中期末教学质量监测数学试题
- 河北省张家口市2026届高三上学期期末教学质量监测数学试题
- 湖南省邵阳市海谊中学2025-2026学年高二上学期12月阶段检测数学试题
- 河北省张家口市2025-2026学年高二上学期期末教学质量监测数学试卷
- 湖南省常德市石门县第一中学2025-2026学年高一上学期元月份阶段性检测数学试题
- 广东省佛山市部分学校2025-2026学年高一上学期12月月考数学试题
- 湖南省教育战略合作学校2025-2026学年高三上学期第二次联考数学试题
- 广东省佛山市南海区2025-2026学年高二上学期学业水平测试(12月)数学试题
-
1、已知、、分别是椭圆的左、右焦点和上顶点,连接并延长交椭圆于点 , 若为等腰三角形,则椭圆的离心率为.
-
2、已知直线 , 若 , 则实数的值为.
-
3、如图.三棱台中,是上一点,平面 , , 则( )
 A、平面 B、平面平面 C、三棱台的体积为 D、若点在侧面上运动(含边界),且与平面所成角的正切值为4,则BP长度的最小值为.
A、平面 B、平面平面 C、三棱台的体积为 D、若点在侧面上运动(含边界),且与平面所成角的正切值为4,则BP长度的最小值为. -
4、已知圆是直线上一动点,过点P作直线PA,PB分别与圆C相切于点A,B,则( )A、圆C上恰有1个点到直线l的距离为 B、|PA|的最小值是 C、|AB|存在最大值 D、|AB|的最小值是
-
5、在三棱锥P-ABC中, , 平面PAB⊥平面ABC,若球O是三棱锥P-ABC的外接球,则球O的表面积为( )A、96π B、84π C、72π D、48π
-
6、如图,在平行六面体中,底面和侧面都是正方形, , 点是与的交点,则( )
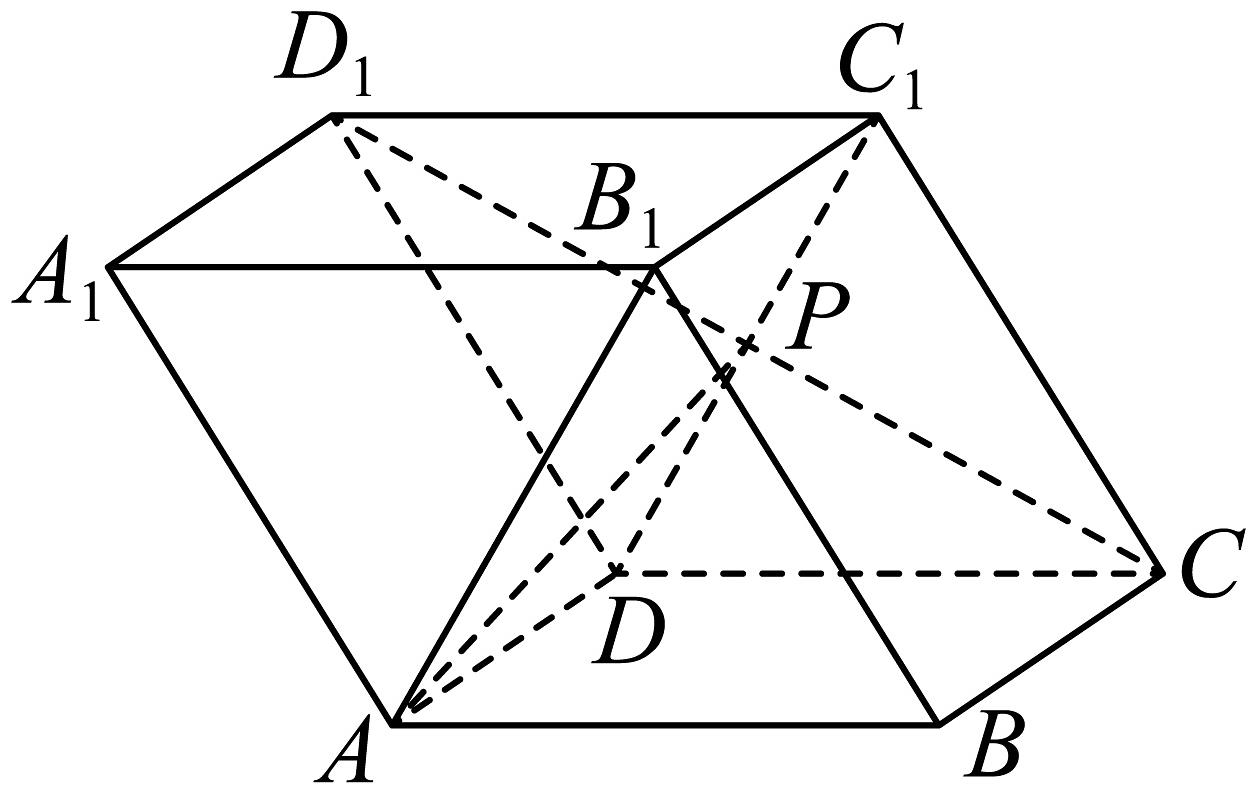 A、 B、2 C、4 D、6
A、 B、2 C、4 D、6 -
7、已知双曲线的离心率为 , 则渐近线方程为( )A、 B、 C、 D、
-
8、已知椭圆:经过点 , 且离心率为 ,
(1)求椭圆的方程;
(2)过点的直线与椭圆交于不同两点、.求证:直线和的斜率之和为定值.
-
9、某同学在研究函数时,给出下列结论:①对任意成立;②函数的值域是;③若 , 则一定有;④函数在上有2个零点.则正确结论的序号是 .
-
10、记面积为 , , , 则.
-
11、民宿旅游逐渐成为一种热潮,山野乡村的民宿也深受广大旅游爱好者的喜爱.对于民宿的改造,窗户面积与地板面积之比越大,采光效果越好.现有一所地板面积为240平方米的民宿需要同时增加窗户和地板的面积,已知地板增加的面积是窗户增加的面积的3倍,且民宿改造后的采光效果不逊于改造前,则改造前的窗户面积最大为平方米.
-
12、已知函数 , 若函数恰有两个零点,则实数m不可能是( )A、 B、 C、1 D、0
-
13、已知椭圆的左、右焦点分别为F1 , F2 , 过F1的直线l1与过F2的直线l2交于点M,设M的坐标为(x0 , y0),若l1⊥l2 , 则下列结论正确的有( )A、 B、 C、 D、
-
14、若函数在上的最大值为4,则的取值范围为( )A、 B、 C、 D、
-
15、设函数 , 若是的极大值点,则a的取值范围是( )A、 B、 C、 D、
-
16、如图,在离地面高的热气球上,观测到山顶处的仰角为 , 山脚处的俯角为 , 已知 , 则山的高度为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、已知双曲线的左、右焦点分别为F1、F2 , 过点F1作圆x2+y2=a2的切线交双曲线右支于点M,若tan∠F1MF2=2,又e为双曲线的离心率,则e2的值为( )A、 B、 C、 D、
-
18、红星幼儿园要建一个长方形露天活动区,活动区的一面利用房屋边墙(墙长),其它三面用某种环保材料围建,但要开一扇宽的进出口(不需材料),共用该种环保材料 , 则可围成该活动区的最大面积为( )A、 B、 C、 D、
-
19、等比数列中 , 公比 , 记(即表示数列的前项之积),中值为正数的个数是( )A、 B、 C、 D、
-
20、圆心为的圆经过点 , , 且圆心在上,
(1)求圆的标准方程;
(2)过点作直线交圆于且 , 求直线的方程.