-
1、 若等腰三角形的一个底角为70°，则它的顶角等于°.
-
2、 如图所示，在△ABC中，在边AB上取一点P，连结CP，在边CP上取一点Q，连结BQ.若△ACP≌△QBP，∠ACP=23°，则∠CBQ的度数为( )
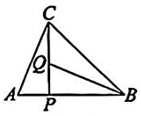A、23° B、22° C、30° D、32° -
3、 如图，等腰△ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于点E，F.若D为BC边的中点，M为线段EF上一动点，则△CDM周长的最小值为( )
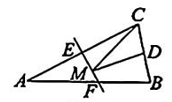A、6 B、8 C、10 D、12 -
4、 下列选项中可以用来证明命题“如果∠1+∠2=90°，那么∠1≠∠2”是假命题的反例是( )A、∠1=30°，∠2=60° B、∠1=30°，∠2=50° C、∠1=∠2=45° D、∠1=40°，∠2=40°
-
5、 下列选项中的命题，是真命题的是( )A、面积相等的两个三角形全等 B、周长相等的两个三角形全等 C、底角相等的两个等腰三角形全等 D、边长相等的两个等边三角形全等
-
6、 用火柴棒摆一个等腰三角形，有两边分别用了2根、7根长度相同的火柴棒，则摆这个等腰三角形需用火柴棒( )A、11根 B、14根 C、16根 D、17根
-
7、 已知三角形的两边长分别是5和9，则这个三角形第三边长可能是( )A、3 B、4 C、5 D、14
-
8、 如图，在平面直角坐标系中，O为原点，点A(0，3)，B(-4，0)，C(4，0).若将点B向右平移10个单位长度，再向上平移4个单位长度，得到对应点D.
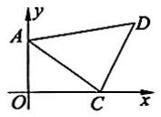(1)、点D的坐标为；(2)、若P是y轴上一动点， 的面积等于的面积，请求出点P的坐标；(3)、若E为x轴上一动点，为等腰三角形，请直接写出点E的坐标. -
9、 如图，为了测量一条两岸平行的河流宽度，由于跨河测量困难，所以三个数学研究小组设计了不同的方案，他们在河南岸的点B处，测得河北岸的一棵树底部点A恰好在点B的正北方向，测量方案如下表：
课题
测量河流宽度
工具
测量角度的仪器(仪器的高度忽略不计)，标杆，皮尺等
小组
第一小组
第二小组
第三小组
测量方案
观测者从点B向正东走到点C，此时恰好测得∠ACB=45°.
观测者从点B向正东走到点E，O是BE的中点，继续从点E沿垂直于BE的EF方向走，直到点A，O，F在一条直线上.
测量示意图
(1)、第一小组认为，河宽AB的长度就是线段的长度；(2)、第二小组方案灵感来源于古希腊哲学家泰勒斯，他们认为只要测得EF的长就是所求河宽AB的长，你认为第二小组的方案可行吗? 如果可行，请给出证明；如果不可行，请说明理由；(3)、请你代表第三小组，设计一个测量方案，把测量方案和测量示意图填入上表，然后指明你画的示意图中，只要测出哪条线段的长，就能推算出河宽AB的长，并说明方案的可行性. -
10、 如图，在平面直角坐标系中， 的顶点A(0，1)，B(3，2)，C(1，4)均在正方形网格的格点上.
(1)、以x轴为对称轴，作的轴对称图形 画出图形，并写出顶点的坐标；(2)、将向左平移3个单位后得到画出图形，并写出顶点的坐标. -
11、 如图，在平面直角坐标系中，点A的坐标是(4，0)，点P在第一象限，且在直线 上.设点P的横坐标为a， 的面积为S.
(1)、求S关于a的函数表达式；(2)、若 ， 求S的值. -
12、 如图，在中， ， 延长CA至点D，延长BA至点E，使得AD，连结BD和CE.求证：
-
13、 解不等式：
-
14、 已知一次函数 的图象不经过第一象限，当 时，y的最大值与最小值的差为5，则k的值为.
-
15、【情境】某快递车从公司出发，到达A驿站，卸完包裹后立即前往B驿站，再卸完包裹后按原路返回公司.快递车行驶速度恒定，在两个驿站卸包裹的时间一样.快递车离公司的路程s与时间t的关系(部分数据)如图所示.
【问题】快递车在每个驿站卸包裹的时间为分钟.
-
16、 如图，在△ABC中，∠ACB=90°，∠BAC=30°，将△ABC绕点C按逆时针方向旋转α角( <α<90°)，得到△A'B'C，设A'C交AB边于点D，连结AA'，若 是等腰三角形，则旋转角α的度数为.
-
17、 若直线l与直线y=-x+1关于y轴对称，则直线l与x轴的交点坐标是.
-
18、 如图，在平面直角坐标系中，已知点A，B的坐标分别为(-4，0)，(0，2).现将线段AB向右平移，使点A与坐标原点O重合，则点B平移后的坐标是.
-
19、 若a>b，则-3a -3b.(填“>”或“<”)
-
20、 如图1，在四边形ABCD中，已知. ， 点P从点A出发，以每秒1个单位长度的速度按A→B→C→D的顺序在边上匀速运动，设点P的运动时间为t秒， 的面积为S，S关于t的函数图象如图2所示，当点P运动到BC的中点时，那么 的面积为( )
A、3 B、4 C、5 D、6