安徽省马鞍山市2017届九年级上册数学期末考试试卷
试卷更新日期:2018-01-23 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,将二次函数 的图象向上平移2个单位,所得图象的表达式为( )
A、 B、 C、 D、2. 三角形在方格纸中的位置如图所示,则 的值是( )
的值是( )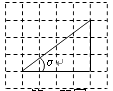 A、 B、- C、 D、3. 如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是( )
A、 B、- C、 D、3. 如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是( ) A、2 cm2 B、4 cm2 C、8 cm2 D、16 cm24. 一个直角三角形的两直角边长分别为 ,其面积为2,则表示 与 之间关系的图象大致为( )A、
A、2 cm2 B、4 cm2 C、8 cm2 D、16 cm24. 一个直角三角形的两直角边长分别为 ,其面积为2,则表示 与 之间关系的图象大致为( )A、 B、
B、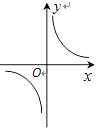 C、
C、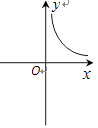 D、
D、 不符合题意
5. 如图,已知等边 的边长为2, 是它的中位线.给出3个结论:
不符合题意
5. 如图,已知等边 的边长为2, 是它的中位线.给出3个结论: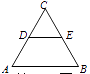
⑴ ;
⑵ ;
⑶ 的面积与 的面积之比为1∶4.其中正确的有( )
A、0个 B、1个 C、2个 D、3个6. 已知二次函数 的 与 的部分对应值如下表:…
-1
0
1
3
…
…
-3
1
3
1
…
则下列判断中正确的是( )
A、拋物线开口向上 B、拋物线与 轴交于负半轴 C、当 时, D、方程 的正根在3与4之间7. 如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 .如果在坡度为0.75的山坡上种树,也要求株距为4 ,那么相邻两树间的坡面距离为( )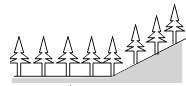 A、5 B、6 C、7 D、88. 如图, 与 ,其中 = , , , .记 的面积为 , 的面积为 ,则下列结论正确的是( )
A、5 B、6 C、7 D、88. 如图, 与 ,其中 = , , , .记 的面积为 , 的面积为 ,则下列结论正确的是( )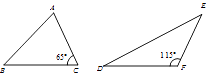 A、 B、 C、 D、无法确定9. 如图,在等边 中, , , 分别是 , , 上的点, , , ,则 的面积与 的面积之比等于( )
A、 B、 C、 D、无法确定9. 如图,在等边 中, , , 分别是 , , 上的点, , , ,则 的面积与 的面积之比等于( )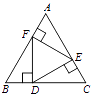 A、1∶3 B、2∶3 C、 ∶2 D、 ∶310. 如图,一次函数 与二次函数 的图象相交于 两点,则函数 的图象可能为( )
A、1∶3 B、2∶3 C、 ∶2 D、 ∶310. 如图,一次函数 与二次函数 的图象相交于 两点,则函数 的图象可能为( )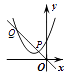 A、
A、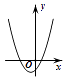 B、
B、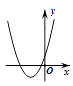 C、
C、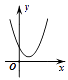 D、
D、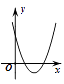
二、填空题
-
11. 若 ,则 .12. 一根竹竿的高2米,影长为1.5米,同一时刻,某住宅楼的影长是30米,则此楼的高度为 .13. 函数 的最大值是 .14. 计算: = .15. 如图,已知 顶点 ,以原点 为位似中心,把 缩小到原来的 ,则与点 对应的点 的坐标是 .
 16. 如图,锐角 中, , , 分别在边 上,且 ∥ ,以 为边向下作矩形 ,设 ,矩形 的面积为 ,则 关于 的函数表达式为 .
16. 如图,锐角 中, , , 分别在边 上,且 ∥ ,以 为边向下作矩形 ,设 ,矩形 的面积为 ,则 关于 的函数表达式为 .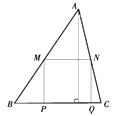 17. 如图,点P是 内一点,过点P分别作直线平行于 的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1,9和49.则△ABC的面积是 .
17. 如图,点P是 内一点,过点P分别作直线平行于 的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1,9和49.则△ABC的面积是 .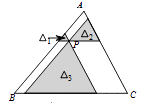 18. 已知二次函数 ( )的图象如上图所示,给出4个结论:
18. 已知二次函数 ( )的图象如上图所示,给出4个结论:① ;② ;③ ;④ .其中正确的是 (把正确结论的序号都填上).
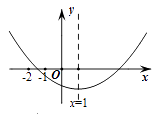
三、解答题
-
19. 已知二次函数图象的顶点为 ,且过点 .求该二次函数的表达式.
20. 如图,已知 是反比例函数 的图象与一次函数 的图象的两个交点.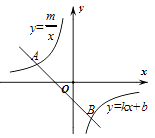 (1)、求此反比例函数和一次函数的表达式;(2)、根据图象写出不等式 的解集.
(1)、求此反比例函数和一次函数的表达式;(2)、根据图象写出不等式 的解集.
21. 如图, 是等边三角形,点 在同一条直线上,且 . (1)、请直接写出图中相似的三角形;(2)、探究 之间的关系,并说明理由.22. 如图,某人在 处仰望山顶 ,测得仰角 ,再往山的方向(水平方向)前进 至 处仰望山顶,测得仰角 .求这座山的高度(人的身高忽略不计). (参考数据:tan31º ≈ , sin31º ≈ , tan39º ≈ , sin39º ≈ )
(1)、请直接写出图中相似的三角形;(2)、探究 之间的关系,并说明理由.22. 如图,某人在 处仰望山顶 ,测得仰角 ,再往山的方向(水平方向)前进 至 处仰望山顶,测得仰角 .求这座山的高度(人的身高忽略不计). (参考数据:tan31º ≈ , sin31º ≈ , tan39º ≈ , sin39º ≈ )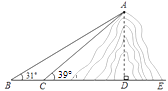 23. 某汽车经销商购进 两种型号的低排量汽车,其中 型汽车的进货单价比 型汽车的进货单价多2万元,经销商花50万元购进 型汽车的数量与花40万元购进 型汽车的数量相等.销售中发现 型汽车的每周销量 (台)与售价 (万元/台)满足函数关系式 , 型汽车的每周销量 (台)与售价 (万元/台)满足函数关系式 .
23. 某汽车经销商购进 两种型号的低排量汽车,其中 型汽车的进货单价比 型汽车的进货单价多2万元,经销商花50万元购进 型汽车的数量与花40万元购进 型汽车的数量相等.销售中发现 型汽车的每周销量 (台)与售价 (万元/台)满足函数关系式 , 型汽车的每周销量 (台)与售价 (万元/台)满足函数关系式 .
(1)、求 两种型号的汽车的进货单价;(2)、已知 型汽车的售价比 型汽车的售价高2万元/台,设 型汽车售价为 万元/台.每周销售这两种车的总利润为 万元,求 与 的函数关系式, 两种型号的汽车售价各为多少时,每周销售这两种车的总利润最大?最大总利润是多少万元?
24. 如图1, 与 为等腰直角三角形, 与 重合, , .固定 ,将 绕点 顺时针旋转,当 边与 边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设 (或它们的延长线)分别交 (或它们的延长线)于点 ,如图2.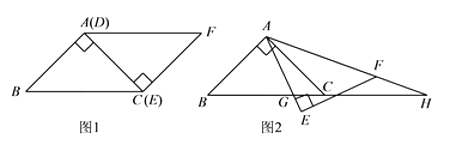 (1)、证明: ;(2)、当 为何值时, 是等腰三角形?
(1)、证明: ;(2)、当 为何值时, 是等腰三角形?