-
1、 把命题“全等三角形的对应角相等”改写成“如果……那么……”的形式为.
-
2、 命题“如果a⊥c，b⊥c，那么a∥b”的条件是( )A、a⊥c B、b⊥c C、a⊥c，b⊥c D、a∥b
-
3、 关于命题“内错角相等，两直线平行”的条件和结论，下列选项中的说法正确的是 ( )A、条件是内错角相等，结论是两直线平行 B、条件是两直线平行，结论是内错角相等 C、条件和结论都是内错角相等 D、条件和结论都是两直线平行
-
4、 下列选项中的语句属于定义的是( )A、若a>b，则a-b>0 B、两直线平行，同位角相等 C、对顶角相等 D、有一个角是直角的三角形叫做直角三角形
-
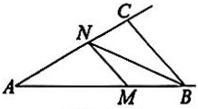
5、如图，在 中， ， M是射线AB上的一个动点，过点M作 交AC于点N.当 是等腰三角形时，求的度数.
-
6、如图，在 中， 点D在边AB上，
(1)、求 的度数；(2)、过点A作 交CD的延长线于点E.求证：是等腰三角形. -
7、如图，在 中， ， CD是AB边上的中线，将 沿直线AC折叠，使点D落在点E处，得到四边形ABCE.求证：.
-
8、 如图，在 的方格纸中，线段AB的两个端点A，B都在小方格的格点上.按要求画一个三角形，使它的顶点在小方格的格点上.
(1)、以线段AB为一腰画一个锐角等腰 ， 在图1中画出示意图；(2)、以线段AB为一腰画一个直角等腰 ， 在图2中画出示意图. -
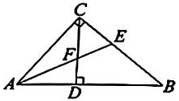
9、 如图，在△ABC中，∠ACB=90°，AB边上的高线CD与∠CAB的平分线AE交于点F.若∠CAE=25°，求∠CFE的度数.
-
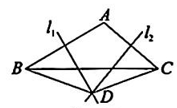
10、 如图，在△ABC中，边AB，AC的垂直平分线交于点D，若∠BDC=140°，则∠BAC的度数为.
-
11、 三角形的三个内角分别为75°，80°，25°，现有一条直线将它分成两个等腰三角形，那么这两个等腰三角形的顶角的度数分别是.
-
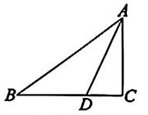
12、 如图所示，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，若AC=6，BC=8，则=.
-
13、 如图所示，将△ABC沿射线AB方向平移得到△BDE.如果∠CAB=48°，∠ABC=100°，那么∠1=°.
-
14、 已知直角三角形的两条直角边长分别为5和12，则其斜边长为.
-
15、 若等腰三角形的一个底角为70°，则它的顶角等于°.
-
16、 如图所示，在△ABC中，在边AB上取一点P，连结CP，在边CP上取一点Q，连结BQ.若△ACP≌△QBP，∠ACP=23°，则∠CBQ的度数为( )
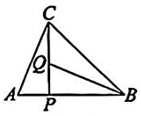A、23° B、22° C、30° D、32° -
17、 如图，等腰△ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于点E，F.若D为BC边的中点，M为线段EF上一动点，则△CDM周长的最小值为( )
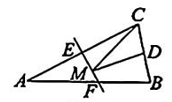A、6 B、8 C、10 D、12 -
18、 下列选项中可以用来证明命题“如果∠1+∠2=90°，那么∠1≠∠2”是假命题的反例是( )A、∠1=30°，∠2=60° B、∠1=30°，∠2=50° C、∠1=∠2=45° D、∠1=40°，∠2=40°
-
19、 下列选项中的命题，是真命题的是( )A、面积相等的两个三角形全等 B、周长相等的两个三角形全等 C、底角相等的两个等腰三角形全等 D、边长相等的两个等边三角形全等
-
20、 用火柴棒摆一个等腰三角形，有两边分别用了2根、7根长度相同的火柴棒，则摆这个等腰三角形需用火柴棒( )A、11根 B、14根 C、16根 D、17根