-
1、在一次高尔夫球的练习中,小成在 O 处击球,其飞行路线满足抛物线 . 其中 y(m) 是球的飞行高度,x(m) 是球飞出的水平距离,结果球离球洞的水平距离还有 2m.
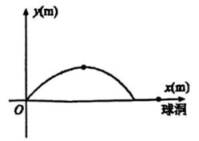 (1)、 请求出抛物线的顶点坐标;(2)、 请求出球洞离击球点的距离;(3)、 若小成再一次从 O 处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线?求出其解析式.
(1)、 请求出抛物线的顶点坐标;(2)、 请求出球洞离击球点的距离;(3)、 若小成再一次从 O 处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线?求出其解析式. -
2、如图,用长为 40cm 的细铁丝围成一个矩形 ABCD(),若这个矩形为黄金矩形(AD 与 AB 之比等于黄金比).
 (1)、 求该矩形的长.(结果保留根号)(2)、 求该矩形的面积.(结果保留根号)
(1)、 求该矩形的长.(结果保留根号)(2)、 求该矩形的面积.(结果保留根号) -
3、口袋里只有8个球,除颜色外都相同. 其中有x个红球,y个白球,没有其他颜色的球,从中任意摸出一个球:(1)、如果摸到红球与摸到白球的可能性相等,分别求x和y的值;(2)、在(1)的条件下,现从布袋中取出若干个白球,并放入相同数量的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是 , 求取走了多少个白球.
-
4、一个斜抛物体的水平运动距离记为x(m),对应高度记为h(m),h与x之间具有函数关系(a,b是常数,).已知当时,;当时,.(1)、 求h关于x的函数表达式.(2)、 求斜抛物体的最大高度和达到最大高度时的水平运动距离
-
5、已知二次函数的图象经过点(-1, 8),(2, -1)。(1)、 求这个二次函数的解析式;(2)、 求这个图象的顶点坐标和对称轴.
-
6、已知a:b:c=3:5:6,且2a+b-c=10,求abc的值.
-
7、小观、小武是某校八年级的同班同学,在升入九年级时,学校打算重新组班,他们将被随机编入A,B,C三个班中的其中一个.(1)、请你用画树状图法或列表法,列出所有可能的结果;(2)、求两人再次成为同班同学的概率.
-
8、 如图,抛物线 与交于点 , 过点 作 轴的平行线,分别交两条抛物线于点 、. 则以下结论,其中正确结论的编号是.

① 无论 取何值, 的值总是正数;② ;③ 当 时,;
④ 当 时,;⑤ .
-
9、 抛物线 与 y 轴交点的坐标为 , 与 x 轴交点的坐标为
-
10、 已知 , 则.
-
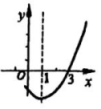
11、 若二次函数 的部分图象如图所示,关于 x 的一元二次方程 的一个解 , 则另一个解 .
-
12、 某十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号灯时,是黄灯的概率为.
-
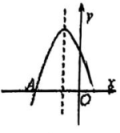
13、 如图是二次函数 图象的一部分,图象过点 A(-3,0),对称轴为直线 , 给出四个结论:
① ;② ;③ ;④ , 其中正确结论是( )
 A、②④ B、①④ C、②③ D、①③
A、②④ B、①④ C、②③ D、①③ -
14、 二次函数 的图象如何平移就得到 的图像( )A、向左平移 1 个单位,再向上平移 3 个单位. B、向右平移 1 个单位,再向上平移 3 个单位. C、向左平移 1 个单位,再向下平移 3 个单位. D、向右平移 1 个单位,再向下平移 3 个单位.
-
15、 在函数 的图像上有三点 , , , 则下列各式中,正确的是( )A、 B、 C、 D、
-
16、 如图,点 C 是线段 AB 的黄金分割点(),则下列结论中正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、 在一个不透明的盒子中装有8个白球,4个黄球,它们除颜色不同外,其余均相同,若从中随机摸出一个球为白球的概率是( )A、 B、 C、 D、
-
18、 已知线段 , , 线段c是a和b的比例中项,则c等于( )A、2 B、4 C、 D、8
-
19、 下列线段能成比例线段的是( )A、1cm, 2cm, 3cm, 4cm B、1cm, cm, cm, 4cm C、cm, cm, cm, 1cm D、2cm, 5cm, 3cm, 4cm
-
20、 抛物线 的对称轴是直线( )A、 B、 C、 D、