-
1、解不等式组:
-
2、计算:.
-
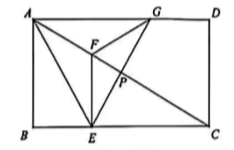
3、如图,在矩形ABCD中,AE平分交BC于点E,交AC于点F,将沿EF折叠得到 , EG交AC于点P,若 , 则.
-
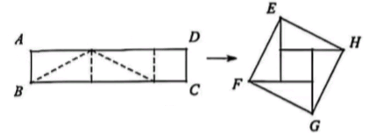
4、如图,将左边矩形纸片ABCD沿虚线剪开并拼接成了右边正方形EFGH,则.
-
5、若扇形圆心角为60°,半径为2,则该扇形的面积为.
-
6、若=2,则x=.
-
7、一个游戏转盘如图所示,红色扇形的圆心角为72°,让转盘自由转动,当转盘停止时,指针落在红色区域的概率是.

-
8、如图,在等腰Rt△ACB中,CA=CB,∠ACB=90°,点D是斜边AB的中点,点E在BD上,连结CE,作AF⊥CE于点F,连结DF,则点E从点D向点B移动过程中(点E不与D、B重合),∠DFE角度的大小为( )
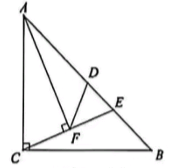 A、由小变大 B、由大变小 C、不变 D、不能确定
A、由小变大 B、由大变小 C、不变 D、不能确定 -
9、如图,矩形ABCD的面积为 , A点的坐标为(2,1),轴,轴,若反比例函数的图像过点B、D,则k的值为( )
 A、 B、 C、5 D、
A、 B、 C、5 D、 -
10、端午节是我国的传统佳节,民间历来有吃粽子的习俗,端午节期间,某商店对一款粽子推出优惠活动,决定每个粽子打八折,打折后120元买到的粽子数量比打折前多了6个,设粽子的原价为x(元/个),可列出方程( )A、 B、 C、 D、
-
11、某公司招聘技术人员,需对应聘者进行测试,测试项目包括基础知识、操作能力、创新能力,并规定上述三项成绩依次按30%,30%,40%的比例计入总成绩,某应聘者的测试成绩统计如下:
项目
基础知识
操作能力
创新能力
成绩
85
90
95
则此应聘者的总成绩是( )
A、90.5 B、90 C、89.5 D、88.5 -
12、如图所示网格中,线段AB是由线段CD位似放大而成,则位似中心是( )
 A、P1 B、P2 C、P3 D、P4
A、P1 B、P2 C、P3 D、P4 -
13、如图, , 若 , 则为( )
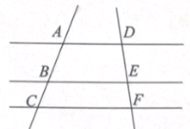 A、 B、 C、 D、
A、 B、 C、 D、 -
14、2024年浙江省GDP总产值为90100亿元,数90100用科学记数法可表示为( )A、 B、 C、 D、
-
15、如图,由6个棱长均为1的立方体组成的几何体,它的左视图为( )
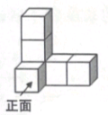 A、
A、 B、
B、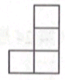 C、
C、 D、
D、
-
16、下列计算正确的是( )A、 B、 C、 D、
-
17、有-2,0, , 四个数,其中最小的数是( )A、-2 B、0 C、π D、
-
18、 小丁和小迪解方程过程分别如下:
小丁:
解:去分母,得x-(x-3)=x-2
去括号,得x-x+3=x-2
合并同类项,得3=x-2
解得x=5
.原方程的解是x=5
小迪:
解:去分母,得x+(x-3)=1
去括号,得x+x-3=1
合并同类项,得2x-3=1
解得х=2
经检验,x=2是方程的增根,原方程无解
你认为小丁和小迪的解法是否正确?若正确,请在框内画“√”,若错误,请在框内画“×”,并写出你的解答过程.
-
19、 解下列方程(组):(1)、(2)、.(3)、解方程:x2-2x=3.
-
20、 解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ▲ .
(Ⅱ)解不等式②,得 ▲ .
(Ⅲ)把不等式①和②的解集在数轴上表示出来;

(Ⅳ)原不等式组的解集为 ▲ .