-
1、如图,在正方形中,对角线与相交于点O, , E是线段上的动点,以为边向左侧作正方形 , 点F始终在直线上,直线与直线交于点N.
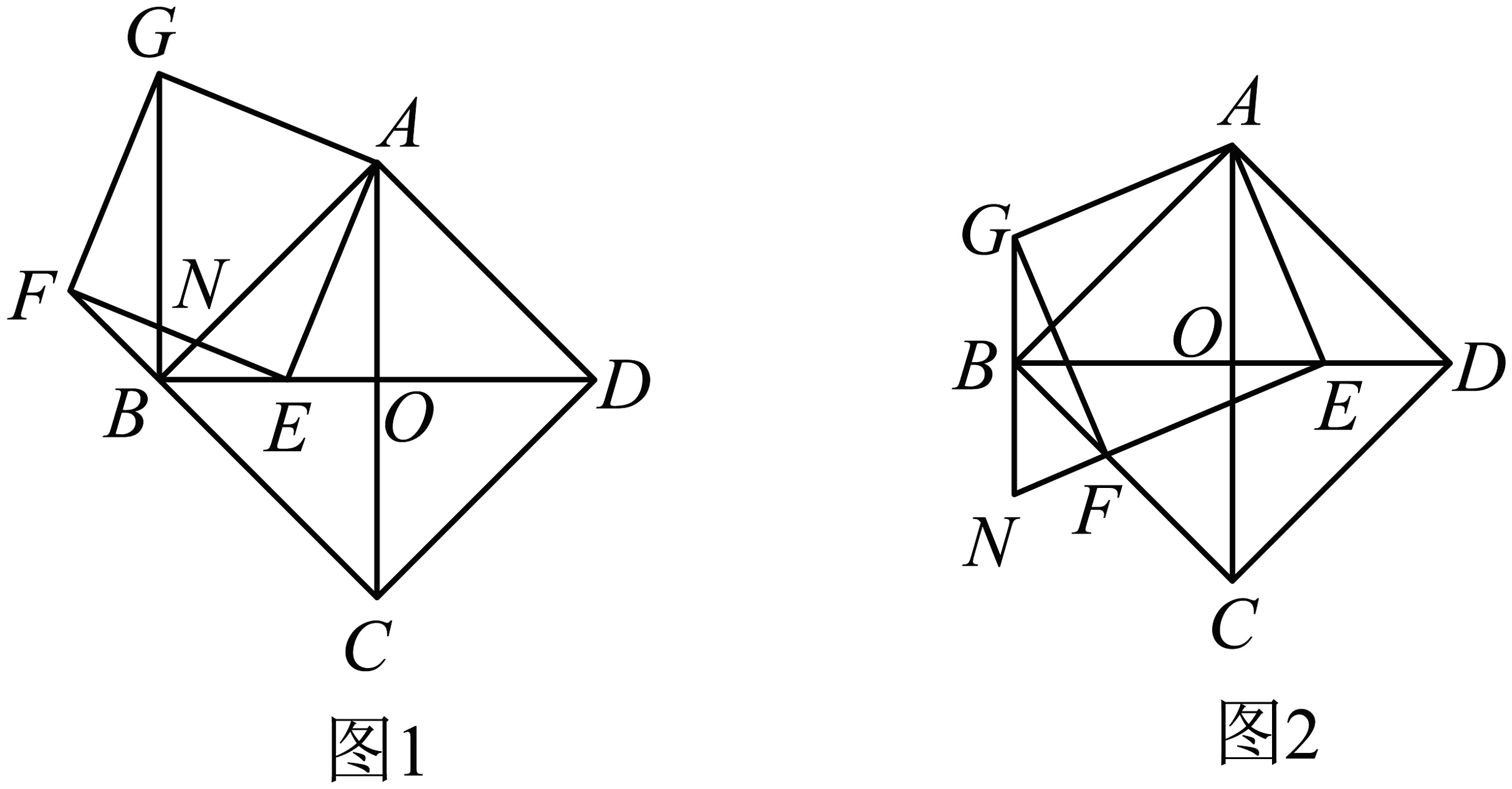 (1)、求证:(在图1或图2中选择一个图形加以证明).(2)、当时,求的长.(3)、试探究,当点E在上运动时,的值是否发生变化?如果不变,请求出这个值;如果变化,请说明理由.
(1)、求证:(在图1或图2中选择一个图形加以证明).(2)、当时,求的长.(3)、试探究,当点E在上运动时,的值是否发生变化?如果不变,请求出这个值;如果变化,请说明理由. -
2、如图,与直线l相离,于点 , 交于点 , 过点作的切线 , 切点为 , 连接并延长交直线于点 .
 (1)、求证:;(2)、若的半径为3, , 求的长.
(1)、求证:;(2)、若的半径为3, , 求的长. -
3、随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷某校数学兴趣小组设计了一份调查问卷,要求每人选且只选-种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
 (1)、这次活动共调查了多少人?在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数是多少?(2)、将条形统计图补充完整,并回答:支付方式的“众数”是(3)、利用这次的调查结果,估计某商场1200名购物者中用现金支付的人数.
(1)、这次活动共调查了多少人?在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数是多少?(2)、将条形统计图补充完整,并回答:支付方式的“众数”是(3)、利用这次的调查结果,估计某商场1200名购物者中用现金支付的人数. -
4、(1)计算:
(2)先化简,再求值: , 其中x满足
-
5、如图,是边长为4的正三角形的外接圆,D为上的一动点,过点A作直线的垂线 . 垂足为E,连接 . 设的长为x,则x的取值范围为

-
6、如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为 .

-
7、“三孩”政策出台后,某家庭积极响应政府号召,已生育三个小孩(生男生女机会均等,且与顺序无关).则这三个小孩中至少有一个女孩的概率是
-
8、不等式的最大正整数解是 .
-
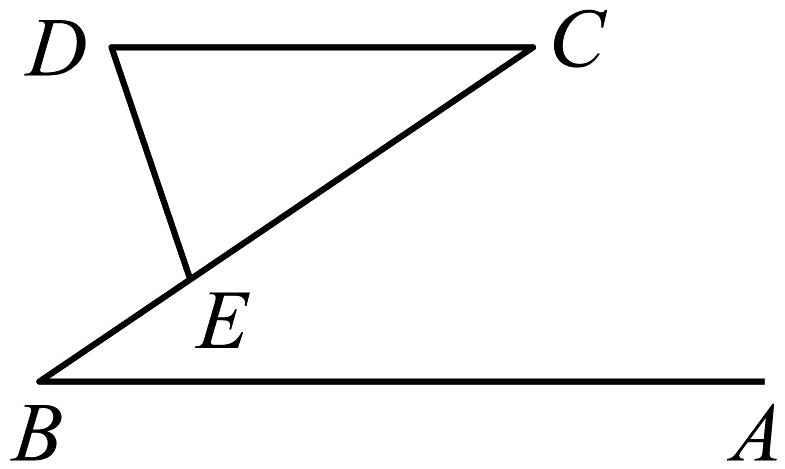
9、如图, , 点E在上, . 若 , 则的度数是
-
10、如图是二次函数 , , 是常数,图象的一部分, 经过点 , 且与y轴的交点在点与之间,函数图象的对称轴为直线 . 下列判断正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图,在菱形中, , 点E,F分别在边 , 上,且 , 连接 , 交于点G,连接 . 现有下列结论:①;②平分;③;④ . 其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
12、如图,在中, , , , I为的内心,于点D,则的长为( )
 A、2 B、1 C、3 D、
A、2 B、1 C、3 D、 -
13、如图,在平面直角坐标系中,原点O是等边三角形的中心.若点A的坐标为 , 将绕着点O逆时针旋转 ,使点A落在点处,则点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、某数学兴趣小组同学进行测量大树高度的综合实践活动,如右图,在点A处测得直立于地面的大树顶端C的仰角为 , 然后沿在同一剖面的斜坡行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面的坡度(或坡比) , 那么大树的高度约为多少?( )
 A、18米 B、13米 C、12米 D、5米
A、18米 B、13米 C、12米 D、5米 -
15、某工厂现有甲种原料 , 乙种原料 , 计划利用这两种原料生产A,B两种产品共50件.已知生产一件A产品需要甲种原料 , 乙种原料;生产一件B产品需要甲种原料 , 乙种原料 . 则符合题意的生产方案共有( )A、2种 B、3种 C、4种 D、5种
-
16、已知关于的一元二次方程有两个不相等的实数根,则的取值范围是( )A、 B、 C、且 D、
-
17、使式子有意义的x的取值范围是( )A、x> 1 B、x≠1 C、x≥-1且x≠1 D、x>-1且x≠1
-
18、下列计算结果正确的是( )A、 B、 C、 D、
-
19、探究与拓展
如图1,在平面直角坐标系中,二次函数的图象与轴交于 , 两点,与轴交于点 , 点的坐标为 , 点是此函数图象在轴上方部分的动点,连接 , . 设点的横坐标为 , 的面积为 , 关于的函数图象如图2所示.
 (1)、请直接写出点的坐标,和图2中的值;(2)、当时,求点的坐标;(3)、当点仅在函数图象上点至点之间的部分运动时,连接 , 交于点 , 则是否存在最大值?若存在,请求出这个最大值并直接写出此时的值;若不存在,请说明理由.
(1)、请直接写出点的坐标,和图2中的值;(2)、当时,求点的坐标;(3)、当点仅在函数图象上点至点之间的部分运动时,连接 , 交于点 , 则是否存在最大值?若存在,请求出这个最大值并直接写出此时的值;若不存在,请说明理由. -
20、
综合与实践
【问题情境】如图1,贴窗花是我国特有的喜庆文化之一,我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形(共同的圆心称为中心),如图2,我们称这种图形为“环花”.
【实践探究】设直线与“环花”从左到右依次交于点 , , , .
(1)如图2,当直线经过中心时,请直接写出线段与的数量关系;
(2)如图3,当直线不经过中心时,请证明(1)中的结论仍然成立;
【问题深化】
(3)如图4,当把“环花”中的两个圆形换成两个相似的菱形时(中心点是这两个菱形对角线的公共交点,且 , , , 四点均在对角线上),类似地形成了“方花”,直线不经中心时,与“方花”从左到右依次交于点 , , , , 求的值.
