-
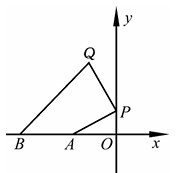
1、 如图,线段OA,OB(OA<OB)的长是x2-6x+8=0的两根,P是y轴正半轴上一点,连结PA,以点P为中心,将线段PA顺时针旋转90°得到线段PQ,连结BQ.当线段BQ取最小值时,点P的坐标是 , 此时线段BQ的最小值为.
-
2、 定义新运算“※”: 对于实数m,n,p,q,有 , 等式的右边是常规的加法和乘法运算, 例如: [2,3] ※[4,5]-2×5+3×4=22.. 若关于x的方程有两个实数根, 则k的取值范围是( )A、且 B、 C、且 D、
-
3、一艘货轮在静水中的航速为40km/h,它以该航速沿江顺流航行120km所用的时间,与以该航速沿江逆流航行80km所用的时间相等,则江水的流速为( )A、5 km/h B、6 km/h C、7km/h D、8 km/h
-
4、我国古代《四元玉鉴》记载了“二果问价”问题,其内容大致如下:用九百九十九文钱,可买甜果苦果共一千个,若·,·,试问:买甜果苦果各几个?
若设买甜果x个,买苦果y个,可列出符合题意的二元一次方程组 ,根据已有信息,题中用“…,·…”表示的缺失的条件应为( )
A、甜果七个用四文钱,苦果九个用十一文钱 B、甜果十一个用九文钱,苦果四个用七文钱 C、甜果四个用七文钱,苦果十一个用九文钱 D、甜果九个用十一文钱,苦果七个用四文钱 -
5、 若 , 则下列结论中,一定正确的是( )A、 B、 C、 D、
-
6、为了解某地区中小学生参加家庭劳动时间情况,某教育部门随机抽取该地区1200名中小学生进行问卷调查,并将调查问卷(部分)和结果描述如下:
调查问卷(部分)
1.你每周参加家庭劳动的时间大约是 ▲ 分钟.
如果你每周参加家庭劳动的时间不足120分钟,请回答第2个问题:
2.影响你每周参加家庭劳动时间的主要原因是 ▲ (单选).
A.没时间
B.家长不舍得
C.不喜欢
D.其它

中小学生每周参加家庭劳动时间x(分)分为6组:①20≤x<40;②40≤x<60;③60≤x<80;④80≤x<100;⑤100≤x<120;⑥120≤x<140.根据以上信息,解答下列问题:
(1)、本次调查中,学生每周参加家庭劳动时间的中位数落在哪一组?(2)、在本次被调查的学生中,选择“不喜欢”的人数为多少?(3)、该教育部门倡议本地区中小学生每周参加家庭劳动时间不少于120分钟.请结合上述统计图,对该地区中小学生每周参加家庭劳动时间的情况作出评价,并提出两条合理化建议. -
7、在阳光中学运动会跳高比赛中,每位选手要进行五轮比赛,张老师对参加比赛的甲、乙、丙三位选手的得分(单位:分,满分10分)进行了数据的收集、整理和分析,信息如下:
信息一:甲、丙两位选手的得分折线图;
信息二:选手乙五轮比赛部分成绩:其中三个得分分别是9.0,8.9,8.3;
信息三:甲、乙、丙三位选手五轮比赛得分的平均数、中位数数据如下:
选手
甲
乙
丙
成绩的平均数(分)
m
9.1
8.9
成绩的中位数(分)
9.2
9.0
n

根据以上信息,回答下列问题:
(1)、请写出表中m,n的值:m= , n=.(2)、从甲、丙两位选手的得分折线图中可知,选手发挥的稳定性更好.(填“甲”或“丙”)(3)、该校现准备推荐一位选手参加市级比赛,你认为应该推荐哪位选手?请说明理由. -
8、为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤80;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:七年级20名学生的竞赛成绩为
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是81,82,84,87,88,89.
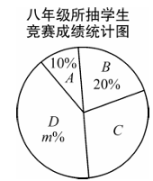
七、八年级所抽学生的竞赛成绩统计表
年级
七年级
八年级
平均数
85
85
中位数
86
b
众数
a
79
根据以上信息,解答下列问题:
(1)、上述图表中a= , b= , m=.(2)、根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可).(3)、该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少. -
9、某校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛.设竞赛成绩为x分,若规定:当x≥90时为优秀,75≤x<75时为一般.现随机抽取30名同学的竞赛成绩如下:
98
88
90
72
100
78
95
92
100
99
84
92
75
100
85
90
9
93
70
92
78
89
91
83
9
98
88
85
90
100
(1)、本次抽样调查的样本容量是 , 样本数据中成绩为“优秀”的频率是.(2)、在本次调查中,A,B,C,D四名同学的竞赛成绩均为100分,其中A,B在九年级,C在八年级,D在七年级,若要从中随机抽取两名同学参加联盟校的党史知识竞赛,请用画树状图或列表的方法求出抽到的两名同学都在九年级的概率,并写出所有等可能结果. -
10、某中学把开展课外经典阅读活动作为一项引领学生明是非、知荣辱、立志向、修言行的德育举措.为了调查活动开展情况,需要了解全校2000名学生一周的课外经典阅读时间.从本校学生中随机抽取100名进行调查,将调查的一周课外经典阅读的平均时间x(h)分为5组:①1≤x<2;②2≤x<3;③3≤x<4;④4≤x<5;⑤5≤x<6并将调查结果用如图所示的统计图描述.

根据以上信息,解答下列问题:
(1)、本次调查中,一周课外经典阅读的平均时间的众数和中位数分别落在第组和第组(填序号);一周课外经典阅读的平均时间达到4小时的学生人数占被调查人数的百分比为;课外经典阅读的平均时间达到4小时的学生有;估计全校一周人.(2)、若把各组阅读时间的下限与上限的中间值近似看作该组的平均阅读时间,估计这100名学生一周课外经典阅读的平均时间是多少?(3)、若把一周课外经典阅读的平均时间达到4小时的人数百分比超过40%作为衡量此次开展活动成功的标准,请你评价此次活动,并提出合理化的建议. -
11、看了《田忌赛马》故事后,小杨用数学模型来分析齐王与田忌的上、中、下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为.
马匹等级
下等
中等
上等
齐王
6
8
10
田忌
5
7
9
-
12、一个不透明的袋中装有除颜色不同外其他均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中.通过大量重复摸球试验后,发现摸到红球的频率稳定在0.4,由此可估计袋中约有红球个.
-
13、某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用.学校数学兴趣小组为给学校提出合理的采购意见,随机抽取了该校学生100人,了解他们喜欢的体育项目,将收集的数据整理,绘制成如下统计图:注:该校每名学生被抽到的可能性相等,每名被抽样调查的学生选择且只选择一种喜欢的体育项目.若该校共有学生1000人,则该校喜欢跳绳的学生大约有人.

-
14、如图所示为2020年2月17~23日某医院每日出院人数折线统计图,相邻两日间日出院人数增长有快慢,其中最大的增长率是.(结果精确到0.1%)

-
15、某校女子排球队队员的年龄分布如下表:
年龄(岁)
13
14
15
人数
4
7
4
则该校女子排球队队员的平均年龄是岁.
-
16、一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这五个数字中一定没有出现数字6的是( )A、中位数是3,众数是2 B、平均数是3,中位数是2 C、平均数是3,方差是2 D、平均数是3,众数是2
-
17、如图所示的电路中,当随机闭合开关 , , 的两个时,灯泡能发光的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、据统计,数学家群体是一个长寿群体,某研究小组随机抽取了收录约2200位数学家的《数学家传略辞典》中部分90岁及以上的长寿数学家的年龄为样本,对数据进行整理与分析,得到的统计图表(部分数据)如下,下列结论中,错误的是( )

年龄范围(岁)
人数(人)
90~91
25
92~93
94~95
96~97
11
98~99
10
100~101
m
A、该小组共统计了100名数学家的寿命 B、统计表中m的值为5 C、长寿数学家寿命在92~93岁的人数最多 D、《数学家传略辞典》中收录的寿命在96~97岁的数学家估计有110人 -
19、如图所示,小球从A入口往下落,在每个交叉口都有向左下或向右下两种可能,且可能性相等,则小球从E出口落出的概率是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A、 B、 C、 D、