河北省石家庄四十二中2017年中考数学模拟试卷
试卷更新日期:2017-11-07 类型:中考模拟
一、选择题:
-
1. 时代超市出售的三种品牌月饼袋上,分别标有质量为:(500±5)g、(500±10)g、(500±20)g的字样,从中任意拿出两袋,它们的质量最多相差( )A、10g B、20g C、30g D、40g2. (am)m•(am)2不等于( )A、(am+2)m B、(am•a2)m C、 D、(am)3•(am﹣1)m3. 在平面直角坐标系中,点P(1,2)关于原点对称的点的坐标是( )A、(﹣1,﹣2) B、(﹣1,2) C、(1,﹣2) D、(2,1)4. 如果( )2÷( )2=3,那么a8b4等于( )A、6 B、9 C、12 D、815. 下列函数中,是一次函数的有( )
①y=πx ②y=2x﹣1 ③y= ④y=2﹣3x ⑤y=x2﹣1.
A、4个 B、3个 C、2个 D、1个6. 如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为( ) A、9 B、10 C、11 D、127. 要使式子 有意义,则x的取值范围是( )A、x>0 B、x≥﹣2 C、x≥2 D、x≤28. 如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )
A、9 B、10 C、11 D、127. 要使式子 有意义,则x的取值范围是( )A、x>0 B、x≥﹣2 C、x≥2 D、x≤28. 如图,图中的几何体是将圆柱沿竖直方向切掉一半后,再在中心挖去一个圆柱得到的,则该几何体的左视图是( )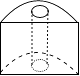 A、
A、 B、
B、 C、
C、 D、
D、 9. 在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )A、1cm<AB<4cm B、5cm<AB<10cm C、4cm<AB<8cm D、4cm<AB<10cm10. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
9. 在等腰△ABC中,AB=AC,其周长为20cm,则AB边的取值范围是( )A、1cm<AB<4cm B、5cm<AB<10cm C、4cm<AB<8cm D、4cm<AB<10cm10. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )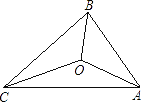 A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②﹣a<b;③a+b>0;④c﹣a<0中,错误的个数是( )个.
A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②﹣a<b;③a+b>0;④c﹣a<0中,错误的个数是( )个.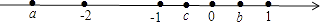 A、1 B、2 C、3 D、412. 甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时.设原来的平均速度为x千米/时,可列方程为( )A、 + =2 B、 ﹣ =2 C、 + = D、 ﹣ =13. 下列各组数,可以作为直角三角形的三边长的是( )A、2,3,4 B、7,24,25 C、8,12,20 D、5,13,1514. 方程x2+6x﹣5=0的左边配成完全平方后所得方程为( )A、(x+3)2=14 B、(x﹣3)2=14 C、(x+3)2=4 D、(x﹣3)2=415. 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE,BC交于N、M,则下列式子中错误的是( )
A、1 B、2 C、3 D、412. 甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时.设原来的平均速度为x千米/时,可列方程为( )A、 + =2 B、 ﹣ =2 C、 + = D、 ﹣ =13. 下列各组数,可以作为直角三角形的三边长的是( )A、2,3,4 B、7,24,25 C、8,12,20 D、5,13,1514. 方程x2+6x﹣5=0的左边配成完全平方后所得方程为( )A、(x+3)2=14 B、(x﹣3)2=14 C、(x+3)2=4 D、(x﹣3)2=415. 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE,BC交于N、M,则下列式子中错误的是( )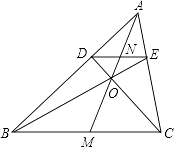 A、 = B、 = C、 = D、 =16. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A、 = B、 = C、 = D、 =16. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )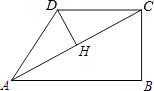 A、
A、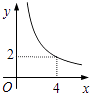 B、
B、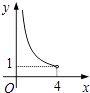 C、
C、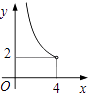 D、
D、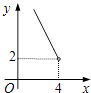
二、填空题:
-
17. 若的平方根为±3,则a= .
18. 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则 的值等于 .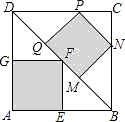
三、计算题:
-
19. ﹣0.52+ ﹣|﹣32﹣9|﹣(﹣1 )3× .20. 计算:3﹣(﹣2)×(﹣1)﹣8×(﹣ )2÷|﹣3+1|.
四、解答题:
-
21. 如右图,已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
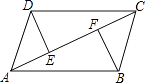 (1)、试证明:DE=BF;
(1)、试证明:DE=BF;
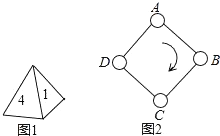
(2)、连接DF,BE,猜想DF与BE的关系?并证明你的猜想的正确性.22. 如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,求△ABD的周长.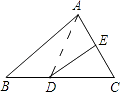 23. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
23. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
 (1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?24. 在“六城”同创活动中,为努力把我市建成“国家园林城市”,绿化公司计划购买A,B,C三种绿化树共800株,用20辆货车一次运回,对我市城区新建道路进行绿化.按计划,20辆货车都要装运,每辆货车只能装运同一种绿化树,且必须装满.根据下表提供的信息,解答以下问题:
(1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?24. 在“六城”同创活动中,为努力把我市建成“国家园林城市”,绿化公司计划购买A,B,C三种绿化树共800株,用20辆货车一次运回,对我市城区新建道路进行绿化.按计划,20辆货车都要装运,每辆货车只能装运同一种绿化树,且必须装满.根据下表提供的信息,解答以下问题:绿 化 树 品 种
A
B
C
每辆货车运载量(株)
40
48
32
每株树苗的价格(元)
20
50
30
(1)、设装运A种绿化树的车辆数为x,装运B种绿化树的车辆数为y,求y与x之间的函数关系式;(2)、如果装运每种绿化树的车辆数都不多于8辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)、若在“六城”同创活动中要求“厉行节约”办实事,则应采用(2)中的哪种安排方案?为什么?25. 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据: ≈1.414, ≈1.732)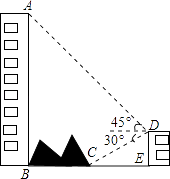
五、综合题:
-
26. 如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.
 (1)、求点A的坐标(用m表示);(2)、求抛物线的解析式;(3)、设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC(AC+EC)为定值.
(1)、求点A的坐标(用m表示);(2)、求抛物线的解析式;(3)、设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC(AC+EC)为定值.