相关试卷

1、已知关于 $x$ 的方程 $x^{2} - 6 x + m = 0$ 有两个不相等的实数根，则实数 $m$ 的取值范围是（）

A、 $m < 9$ B、 $m < - 9$ C、 $m > 9$ D、 $m > - 9$

查看解析
2、下列新能源汽车车标既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看解析
3、2024年我国新能源汽车年产量突破13000000辆，数据13000000用科学记数法表示为（）

A、 $0.13 \times 10^{8}$ B、 $1.3 \times 10^{7}$ C、 $13 \times 10^{6}$ D、 $1.3 \times 10^{6}$

查看解析
4、如图，在平面直角坐标系中，点P为y轴上一点，⊙P交y轴于点A，点B，交x轴的正半轴于点C，AD平分∠BAC交⊙P于点D，过点D作EF⊥AC于点E，交y轴于点F．

(1)、求证：EF为⊙P的切线；

(2)、若A(0，−1)，C( $\sqrt{3}$ ， 0)，求图中阴影部分的面积．

查看解析
5、随着劳动教育的开展，某学校在校园开辟了一块劳动教育基地：一面利用学校的墙（墙的最大可用长度为28米），用长为40米的篱笆，围成中间隔有一道篱笆的矩形菜地，在菜地的前端设计了两个宽 1米的小门，便于同学们进入．

(1)、若围成的菜地面积为120平方米，求此时边 $A B$ 的长；

(2)、可以围成的菜地面积最大是多少？

查看解析
6、计算： $- 1^{2020} + \sqrt{{(- 2)}^{2}} - \sqrt[3]{27} + |2 - \sqrt{3}|$

查看解析
7、如图是一个游戏装置，四边形 $A B O D$ 是正方形，点光源 $E$ 为 $O B$ 的中点．点 $P$ 、点 $Q$ 为 $A D$ 的三等分点， $P Q$ 是一个感光元件．若从点 $E$ 发出的光线照向平面镜 $O D$ ，其反射光线照射到 $P Q$ 上（含端点），该感光元件就会发光．已知点 $E (- 3, 0)$ ，反射光线所在直线为 $y = k x + b$ ，当感光元件发光时， $b$ 的取值范围为．

查看解析
8、若 $x = a$ 是一元二次方程 $x^{2} - 6 x - 2022 = 0$ 的一个根，则 $a^{2} - 6 a + 1$ 的值是．

查看解析
9、设 $A (- 3, y_{1}), B (- 2, y_{2}), C (3, y_{3})$ 是抛物线 $y = - x^{2} - 2 x + c$ 上的三点，则 $y_{1}, y_{2}, y_{3}$ 的大小关系为（　　）

A、 $y_{3} > y_{2} > y_{1}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{2} > y_{1} > y_{3}$

查看解析
10、光线由空气射入清澈的水面时会在水面发生镜面反射，在射入水中后会发生折射现象．如图入射光线 $A P$ 在射入水面 $P$ 点的反射光线为 $P Q$ ，折射光线为 $P B$ ，若反射光线与折射光线夹角为 $80 °$ ，入射光线与折射光线夹角为 $160 °$ ，则入射光线与水平面的夹角为多少度？（　　）

A、 $40 °$ B、 $20 °$ C、 $60 °$ D、 $35 °$

查看解析
11、下列说法正确的是（）

A、圆的内接平行四边形一定是正方形 B、平分弦的直径垂直弦 C、圆的切线一定垂直于半径 D、任何一个三角形的内心一定在三角形内

查看解析
12、如图1，在平面直角坐标系 $x O y$ 中，抛物线： $y = a x^{2} + b x + 6 (a \neq 0)$ 与 $x$ 轴交于 $A$ ， $B$ 两点（点 $B$ 在点 $A$ 的左侧），与 $y$ 轴交于点 $C$ ，连接 $B C$ ，作直线 $A C$ ，点 $A$ 的坐标为 $(6, 0)$ 且 $S_{△ A B C} = 24$ ．

(1)、求抛物线的表达式；

(2)、若点 $P$ 在抛物线第一象限图象上，线段 $E F$ （点 $F$ 在点 $E$ 的左侧）是直线 $A C$ 上一段长度为 $\sqrt{2}$ 的动线段， $y$ 轴上一点 $Q (0, 2)$ ，连接 $Q E$ ， $Q F$ ， $P E$ ， $P F$ ，若四边形 $Q E P F$ 为平行四边形，求 $E$ 点的坐标；

(3)、动直线 $y = k x - 5 k + \frac{3}{2} (k \neq 0)$ 图象交该抛物线于 $M$ ， $N$ 两点，以 $M N$ 为直径作圆与抛物线始终交于一定点 $T$ ，求出点 $T$ 的坐标．

查看解析
13、阅读下面三段素材，完成以下任务：
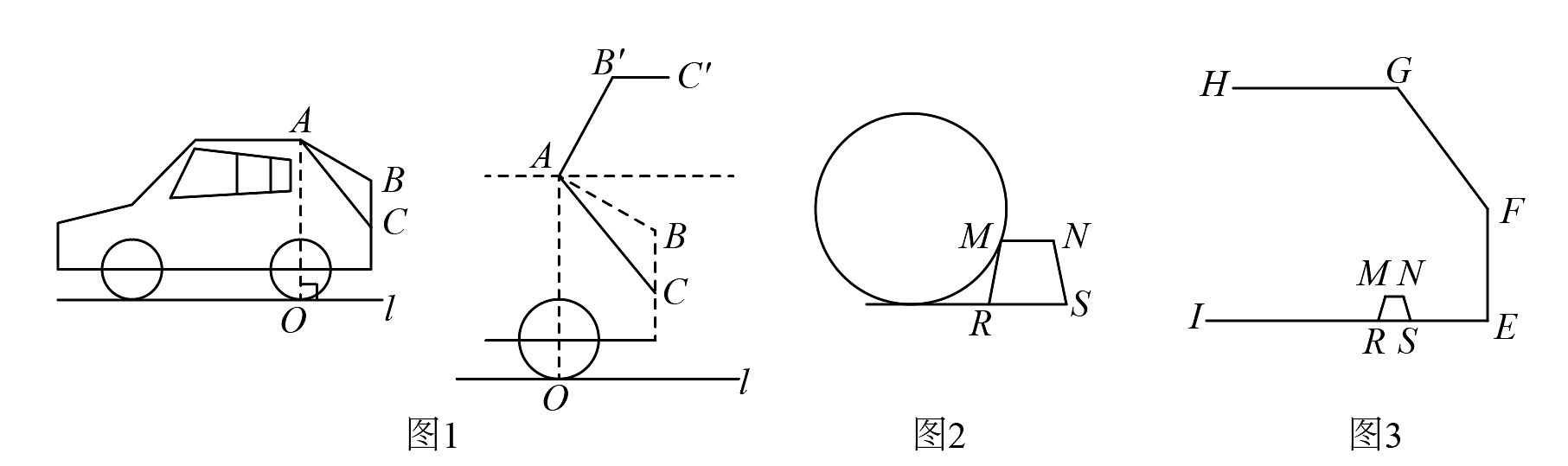
素材一：图1是某越野车的侧面示意图，图2是打开后备箱时的示意图，已知 $A B = lm$ ， $B C = \frac{1}{50} \sqrt{613} m$ ，连接AC， $∠ B A C = 20 °$ ，该车的高度 $A O = 1.7 m$ ，其中O为轮胎与地面的切点（ $A O ⊥$ 地面l）．当后备箱打开到最大时， $A B^{'}$ 与水平面的夹角 $∠ B^{'} A D = 60 °$
素材二：挡车器可以有效提醒正在倒车的驾驶员．使其不能再继续倒车．防止发生意外．对于保障停车场安全管理起到了重要的作用．当车恰好停在挡车器位置时，轮胎与挡车器的位置关系如图2所示．挡车器上的点M在轮胎所对圆上，轮胎与地面相切于点O．如图，某款挡车器 $M N = 8 cm$ ， $R S = 10 cm$ ， $M R = NS$ ．高 $10 cm$ ．
素材三：图3是某厂家的露天停车棚的侧视图．顶棚HG与与支撑杆夹角即 $H G F = 127 °$ ， FE与地面IE垂直， $E F = 1.8 m$ ， $G F = 2 m$ ．
参考数据： $tan 37 ° \approx 0.75$ ， $sin 20 ° \approx 0.34$ ， $cos 20 ° \approx 0.94$ ， $\sqrt{3} \approx 1.732$ ．
任务1：求【素材一】中AC的长为_______．
任务2：【素材一】中的越野车停在挡车器位置时，其轮胎所在圆的圆心与挡车器点M的水平距离为 $10 \sqrt{5} cm$ ．则该越野车的轮胎所在圆的半径是多少？
任务3：将【素材一】中的越野车停在【素材三】中的停车棚内，能保证越野车的后备箱盖可以完全打开吗？请说明理由．

查看解析
14、如图， $A B$ 是圆 $O$ 的直径， $A E$ 交圆 $O$ 于点 $F$ ，且与圆 $O$ 的切线 $C D$ 互相垂直，垂足为 $D$ ．

(1)、求证： $∠ E A C = ∠ C A B$ ；

(2)、若 $C D = 4$ ， $tan ∠ B A E = \frac{4}{3}$ ，求线段 $D F$ 的长度．

查看解析
15、计算： $\sqrt{9} - 4 cos 60 ° + {(π - 2025)}^{0} - ∣ - 2 ∣$ ；

查看解析
16、网格中点 $A$ 、 $B$ 、 $C$ 均为格点，且点 $C$ 在坐标轴上，连接 $A C$ 、 $B C$ ， $∠ A C B = 45 °$ ，则满足条件的点 $C$ 有个．

查看解析
17、如图， $B C$ 为 $⊙ O$ 直径，点 $D$ 为 $⊙ O$ 上一点，连接 $O D$ ，过点 $C$ 作 $C A ∥ O D$ 交 $⊙ O$ 于点 $A$ ，连接 $A B$ ， $B D$ ．若 $∠ A B C = 20 °$ ，则 $∠ C B D$ 的度数为．

查看解析
18、代数式 $\frac{1}{\sqrt{5 - x}}$ 有意义，则x的取值范围为．

查看解析
19、已知 $2 \sqrt{7} < m < \sqrt{39}$ ，则整数 $m =$ ．

查看解析
20、一个点的纵坐标是横坐标的2倍，则称这个点为“二倍点”，在 $- 3 < x < 1$ 的范围内，若二次函数 $y = - x^{2} - x + c$ 的图象上至少存在一个“二倍点”，则c的取值范围是（）

A、 $c \geq - \frac{1}{4}$ B、 $- \frac{1}{4} \leq c < 4$ C、 $- \frac{9}{4} \leq c < - \frac{1}{4}$ D、 $- \frac{9}{4} \leq c < 4$

查看解析

上一页 332 333 334 335 336 下一页跳转