相关试卷

1、某数学研究性学习小组在老师的指导下，利用课余时间进行测量活动，并设计如下测量方案．

活动主题		测算某厂房一面墙的高度与长度
测量工具		皮尺、测角仪、计算器等
活动过程	模型抽象	某工厂的厂房的一面墙，墙面的形状为矩形 $A B C D$ ，其示意图如下：
	测绘过程和数据信息	①在厂房的墙面外取一点 $E$ ，使得点 $A ， B ， E$ 在同一冬克线上．用皮尺测得 $B E = 10$ 米； ②无人机在 $E$ 处，以 $2$ 米/秒的速度竖直向上飞行了 $11$ 秒钟，飞行至 $F$ 处； ③在 $F$ 处测得房顶 $C$ 的俯角 $∠ G F C = 45 °$ ，测得房顶 $D$ 的俯角 $∠ G F D = 14 °$ ； ④用计算器计算得： $\sin 14 ° \approx 0.24$ ， $\cos 14 ° \approx 0.97$ ， $\tan 14 ° \approx 0.25$ ．

请根据表格中提供的信息，解决下列问题，

(1)、求厂房的高度

B C

；

(2)、求厂房的长度

A B

．

查看解析

2、如图，过 $▱ A B C D$ 的顶点 $A ， C$ ，作 $A M ⊥ C D ， C N ⊥ A D$ ，分别交边 $C D$ ， $A D$ 于点 $M ， N$ ，线段 $A M$ 与 $C N$ 交于点 $O$ ，已知___________
请从“① $A O = C O$ ；② $A N = C M$ ”这两组条件中任选一组作为已知条件，填在横线上（填序号），再解决下列问题：
（ $1$ ）证明：四边形 $A B C D$ 是菱形；
（ $2$ ）若 $∠ B = 60 °$ ， $A M = 6$ ，求四边形 $A B C O$ 的面积．

查看解析
3、为践行健康第一教育理念，丰富体育活动项目，某校准备购买一批篮球和排球．已知购买1个篮球和4个排球，共需320元；购买5个篮球和2个排球，共需700元．

(1)、求篮球和排球的单价；

(2)、若学校准备购买篮球、排球共90个，总费用不超过7300元，那么最多能够购买篮球多少个？

查看解析
4、某校兴趣小组开展“体育锻炼最能让我___________”的问卷调查，要求同学们从“A：享受乐趣；B：增强体质；C：锤炼意志；D：缓解压力；E：预防近视”任选一项填在横线上．调查结束后，根据调查结果，绘制了如下两幅不完整的统计图．
请根据以上信息完成下列问题：

(1)、本次调查学生的人数为___________人，扇形统计图中A组对应扇形的圆心角为___________度；

(2)、补全条形统计图；

(3)、该校共有2400名学生，请你估计该校学生认为“体育锻炼最能让我锤炼意志”的人数．

查看解析
5、先化简，再求值： $(\frac{1}{a - 2} + 1) \div \frac{a - 1}{a^{2} - 4}$ ，其中 $a = 2023$ ．

查看解析
6、计算： $9 tan 30 ° + |\sqrt{3} - 2| - {(\frac{1}{2})}^{- 1} - \sqrt{12}$ ．

查看解析
7、如图，在 $Rt △ A B C$ 中， $∠ C A B = 90 °$ ， $∠ B = 30 °$ ．分别以点 $B$ 和 $C$ 为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧相交于 $E ， F$ 两点．连接 $E F$ ，交边 $A B$ 于点 $D$ ．连接 $C D$ ，则 $∠ B C D$ 的度数为．若 $A C = 10$ ，点 $M$ 是线段 $C D$ 上的一个动点，连接 $A M$ ，则 $A M + \frac{1}{2} C M$ 的最小值是．

查看解析
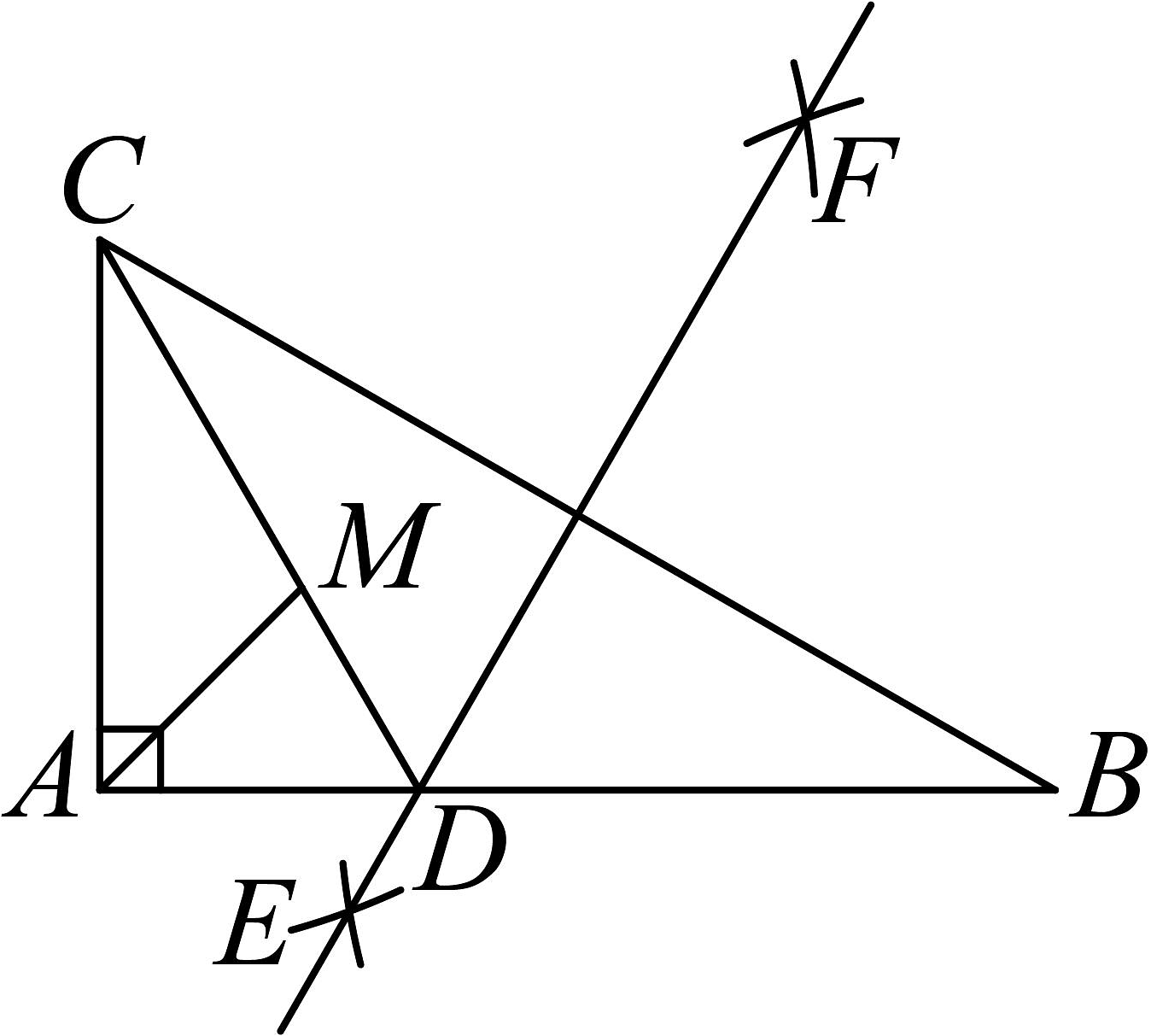
8、《九章算术》中有一道“凫雁相逢”（凫：野鸭）问题：今有凫起南海七日至北海，雁起北海九日至南海，今凫、雁俱起，问何日相逢？如图是凫、雁起飞后，凫、雁距离南海的路程 $s_{1} ， s_{2}$ 关于飞行时间 $t$ 的函数图象，则两函数图象的交点 $M$ 的横坐标是．

查看解析
9、四个相同的烧杯中，分别装有氢氧化钠溶液、稀硫酸溶液、氢氧化钙溶液及蒸馏水，从中任选一个烧杯滴入几滴酚酞溶液，则该烧杯的溶液变成红色的概率是．

查看解析
10、已知电磁波的频率 $f$ 、波长 $λ$ 满足关系： $C = f \times λ$ （ $C$ 为常数）．某种电磁波的频率 $f$ 为 $3 GHz$ 时，波长 $λ$ 为 $100 km$ ．若将该电磁波的波长 $λ$ 调谐为 $20 km$ ，则其频率为 $GHz$ ．

查看解析
11、如图，点 $P$ 是正五边形 $A B C D E$ 边 $B C$ 上一点，过点 $P$ 作直线 $m ∥ A B$ ，则 $∠ 1$ 的度数为．

查看解析
12、如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ 是 $⊙ O$ 上一点．已知 $∠ A B C = 60 ° ， ⊙ O$ 的半径为4，则弦 $B C$ 的长为．

查看解析
13、若代数式 $7 - 5 x$ 的值等于22，则 $x$ 的值为．

查看解析
14、分式 $\frac{7}{x - 42}$ 有意义的条件是．

查看解析
15、定义：若一个函数的图象上存在横坐标和纵坐标互为相反数的点，则称该点为这个函数图象的“相反点”．根据定义，下列说法错误的是（）

A、 $(0, 0)$ 为函数 $y = x$ 图象的“相反点” B、函数 $y = - \frac{3}{x}$ 的图象存在两个“相反点” C、 $(0, 0)$ 为函数 $y = x^{2}$ 的图象上唯一的“相反点” D、当 $m > \frac{5}{4}$ 时，函数 $y = {(x - m)}^{2} - 1$ 的图象上无“相反点”

查看解析
16、判断命题“对任意实数 $a$ ，都有 ${(a + 1)}^{2} > 0$ ”是假命题，只需要举出反例，反例中的 $a$ 可以是（）

A、 $2$ B、 $1$ C、 $0$ D、 $- 1$

查看解析
17、如图，两张相同的宽为 $4 cm$ 的矩形纸片叠放在一起，点 $O$ 是纸片中的任意一点．将一张纸片绕着点 $O$ 逆时针旋转 $α ° (0 < α < 180)$ ，则旋转过程中，两张纸片重叠部分（即四边形 $A B C D$ ）面积的最小值是（）

A、8 ${cm}^{2}$ B、8 $\sqrt{3} {cm}^{2}$ C、 $16 {cm}^{2}$ D、 $32 {cm}^{2}$

查看解析
18、已知点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2}) ， C (x_{3} ， y_{3})$ 在正比例函数 $y = - 5 x$ 的图象上，且 $x_{1} > x_{2} > x_{3}$ ，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{3} > y_{2} > y_{1}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{3} > y_{1} > y_{2}$

查看解析
19、某班的 $7$ 名同学 $1$ 分钟仰卧起坐的成绩（单位：次）分别为： $42 ， 48 ， 45 ， 43 ， 39 ， 48 ， 50$ ，这组数据的中位数是（）

A、 $41$ B、 $43$ C、 $44$ D、 $45$

查看解析
20、下列计算正确的是（）

A、 $5 x - 3 x = 2$ B、 $6 x \cdot 7 x^{2} = 42 x^{2}$ C、 ${(x^{4})}^{3} = x^{12}$ D、 $x^{8} \div x^{2} = x^{4}$

查看解析

上一页 331 332 333 334 335 下一页跳转