相关试卷

1、如图是上海今年春节七天最高气温（℃）的统计结果，这七天最高气温的众数和中位数是（）

A、15，17 B、17，17 C、17，14 D、17，15

查看解析
2、要使 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x≤2 B、x>1 C、x≥0 D、x≥2

查看解析
3、如图：

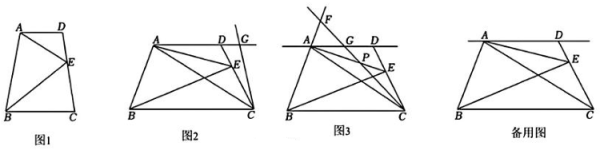(1)、【尝试应用】如图1，在四边形ABCD中，AD//BC，点E是线段CD上一点.∠AEB=70°，∠DAE=30°，求∠CBE的度数；

(2)、【拓展提高】如图2，在四边形ABCD中，AD//BC，点E是线段CD上一点.若AE平分∠DAC，∠CAB=∠ABC.
①试求出∠BAE的度数；
②已知∠AEB=∠ABE，∠EBC=30°，点G是直线AD上的一个动点，连接CG并延长.
Ⅰ.若CA恰好平分∠BCD，当CG与四边形ABCD中一边所在直线垂直时，∠ACG= ▲ .
Ⅱ.如图3，若CG是∠ACD的平分线与BA的延长线交于点F，与AE交于点P，且∠BFC=α°，则∠ADC= ▲ （用含α的代数式表示）.

查看解析

4、根据以下信息，探索解决问题：

背景：为了提高产品的附加值，某公司计划将研发生产的1500件新产品进行加工后再投放市场，每天满工作量情况下，甲、乙两个工厂加工数量及每件加工费用保持稳定不变，公司派出相关人员分别到这两间工厂了解情况，获得如下信息，
信息1	每天满工作量情况下，乙工厂每天加工数量是甲工厂每天加工数量的1.5倍；
信息2	每天满工作量情况下，甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息3	每天满工作量情况下，甲工厂加工1天，乙工厂加工2天共需要10000元：甲工厂加工2天，乙工厂加工3天共需要16100元.
问题解决
问题1	设每天满工作量情况下，甲工厂每天加工数量为x件，结合信息1可得：乙工厂每天加工数量为 ▲ 件（请用x的代数式表示）.
问题2	每天满工作量情况下，求甲工厂每天能加工多少件新产品？
问题3	公司将1500件新产品交给甲、乙两工厂一起加工，发现这批新产品的平均加工费用为整数，两工厂加工的时间之和不是整数，请问交给甲工厂多少件新产品进行加工？

查看解析

5、用若干块如图所示的正方形或长方形纸片拼成图（1）和图（2）.

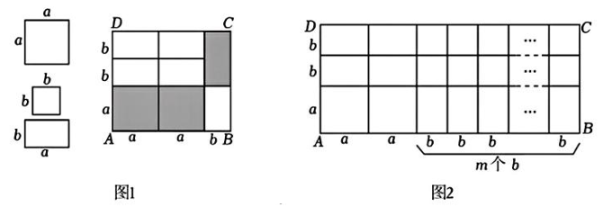(1)、如图1，若长方形ABCD的面积为56，其中阴影部分的面积为26，a>b，求a-b的值.

(2)、如图2，若AD的长度为6，AB的长度为n.
①当m= ， n=时，a，b的值有无数组；
②当m ， n时，a，b的值不存在.

查看解析
6、如图，已知AB//CD，AD平分∠EAC，∠B=∠D.

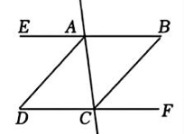(1)、请说明AD//BC：

(2)、若∠DAC=（2x+15）°，∠B=（105-3x）°，求∠D的度数.

查看解析
7、如图，在10×8的正方形网格中，每个小正方形的边长为1，其顶点称为格点，格点△ABC与点D的位置如图所示.

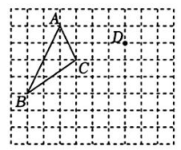(1)、平移格点△ABC，画出平移后的格点△DEF（点A，B，C的对应点分别为点D，E，F）；

(2)、连接AD，CF，则线段AD与线段CF的关系是.

(3)、四边形ADFC的面积为.

查看解析
8、计算下列各题：

(1)、 $(\frac{1}{2})^{- 1} - (- 1)^{2023} + (\sqrt{2} - 1)^{0}$ ；

(2)、 $4 x (x - 6) - (2 x - 1) (2 x + 1)$

查看解析
9、用面积都为1的长方形纸片①、②围成长方形ABCD，如图所示，其中四边形MNPQ也是长方形.设AE=x，DE=y，且x>y·

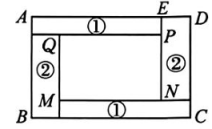(1)、AB=.

(2)、若x²-3xy+y²=0，则 $\frac{S_{长方形 A B C D}}{S_{长方形 P Q M N}}$ =.

查看解析
10、关于x的分式方程 $\frac{2 - x}{x - 4} = \frac{a}{4 - x} - 2$ 有增根，则ａ的值是.

查看解析
11、如图是路灯维护工程车的工作示意图，工作篮底部与支撑平台平行，若∠1=30°，则∠2+∠3的度数为度.

查看解析
12、如果a-b+3=0，那么代数式2-3a+3b的值是.

查看解析
13、七年级某班有48名学生，所在教室有6行8列座位，用（m，n）表示第m行第n列的座位，新学期准备调整座位.设某个学生原来的座位为（m，n），若调整后的座位为（i，j），则称该生作了平移[a，b]=[m-i，n-j]，并称a+b为该生的位置数.某生的位置数为8，当m+n取最小值时，则mn的最大值为（）

A、25 B、30 C、36 D、48

查看解析
14、《九章算术》卷八方程第十题原文为“今有甲、乙二人持钱不知其数.甲得乙半而钱五十；乙得甲太半而亦钱五十.问甲、乙持钱各几何？”题目大意是：现有甲、乙两人，不知分别持有多少钱.如果把乙的钱数的 $\frac{1}{2}$ 给甲，则甲的钱为50；如果把甲的钱数的 $\frac{2}{3}$ 给乙，则乙的钱也是50。问甲、乙两人所持的钱各是多少？设甲、乙两人分别持有的钱是x和y，则可列方程组为（）

A、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ B、 ${\begin{array}{l} \frac{1}{2} x + y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ C、 ${\begin{array}{l} \frac{1}{2} x + y = 50 \\ \frac{2}{3} y + x = 50 \end{array}$ D、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ \frac{2}{3} y + x = 50 \end{array}$

查看解析
15、下列各因式分解正确的是（）

A、-x²+4x=-x（x+4） B、x²+2x-1=（x-1）² C、4x²-4x+1=（2x-1）² D、x²-4x=2（x+2）（x-2）

查看解析
16、如图，有一条直的等宽纸带，按图折叠时形成一个30°的角，则重叠部分的∠α等于（）

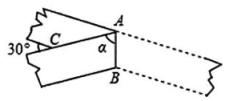A、85° B、75° C、65° D、60°

查看解析
17、已知方程 $3 x - 2 y = 5$ ，把它变形为用含x的代数式表示y，正确的是（）

A、 $y = \frac{- 3 x - 5}{2}$ B、 $y = \frac{3 x + 5}{2}$ C、 $y = \frac{- 3 x + 5}{2}$ D、 $y = \frac{3 x - 5}{2}$

查看解析
18、分式 $\frac{1}{x - 2}$ 有意义，则x的取值范围为（）

A、 $x \neq 0$ B、 $x \neq 2$ C、 $x \neq 0$ 且 $x \neq 2$ D、x为一切实数

查看解析
19、世界上最轻的昆虫是膜翅目缨小蜂科的一种卵蜂，质量只有0.000005克，数0.000005用科学记数法表示为（）

A、 $- 5 \times 1 0^{6}$ B、 $5 \times 1 0^{- 5}$ C、 $5 \times 1 0^{- 6}$ D、 $5 \times 1 0^{- 7}$

查看解析
20、如图：

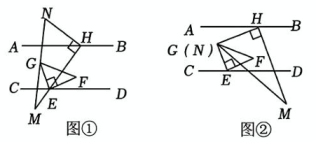(1)、【创设情境】在初一数学活动课上，老师带领学生用一副直角三角尺进行“玩转三角尺”的探究活动.老师让同学们将两把直角三角尺EFG和HMN（∠GEF=∠MHN=90°，∠MNH=60°，∠HMN=30°，∠EGF=∠EFG=45°），已知AB//CD.如图①，把三角尺EFG的直角顶点E放在直线CD上，把三角尺HMN的直角顶点H放在直线AB上，HM经过点E.
若∠GEM=120°，∠DEF=20°，求∠AHN的度数：

(2)、【操作探究】
如图②，绕点H逆时针旋转三角尺HMN，恰好可以使得点G与点N重合，此时测得∠FGM=20°，请你说明∠AHG与∠DEF之间的数量关系；

(3)、【深度探究】
在（1）的条件下，将三角尺GEF绕E点以每秒3°的速度按逆时针方向，同时将三角尺HMN绕H点以每秒2°的速度按顺时针方向旋转，设旋转时间为（0≤t≤60）.当HN与△
EGF的一边平行时，求t的值.

查看解析

上一页 330 331 332 333 334 下一页跳转