-
1、如图,点是边上一点(不与重合),连接 .
 (1)、尺规作图:以为圆心,长为半径作弧,交于点 , 连接(要求在图中作出图形,标明字母);(2)、在(1)的基础上,判断与的位置关系,并说明理由.
(1)、尺规作图:以为圆心,长为半径作弧,交于点 , 连接(要求在图中作出图形,标明字母);(2)、在(1)的基础上,判断与的位置关系,并说明理由. -
2、某餐厅为了解线上外卖服务中用户的需求,提升服务质量,随机抽取200名外卖用户进行问卷调查,调查问卷如下:
XX餐厅外卖服务满意度调查
1.您对本餐厅外卖服务的整体评价为__________.(单选)
A.满意 B.一般 C.不满意
如果您对本餐厅外卖服务的整体评价为“一般”或“不满意”,请回答第2个问题:
2.您认为本餐厅最需要改进的地方为__________.(单选)
A.餐品味道 B.配送速度 C.包装质量 D.售后服务
该餐厅相关工作人员将这200份调查问卷的结果整理后,制成如下统计图:
 (1)、如果将整体评价中“满意”“一般”“不满意”分别赋分为5分、3分、2分,则该餐厅此次调查中整体评价分数的中位数为__________分,平均数为__________分.(2)、在此次调查中,认为该餐厅最需要在配送速度上进行改进的人数是多少.(3)、请你根据此次调查结果,对该餐厅外卖服务提出两条合理的建议.
(1)、如果将整体评价中“满意”“一般”“不满意”分别赋分为5分、3分、2分,则该餐厅此次调查中整体评价分数的中位数为__________分,平均数为__________分.(2)、在此次调查中,认为该餐厅最需要在配送速度上进行改进的人数是多少.(3)、请你根据此次调查结果,对该餐厅外卖服务提出两条合理的建议. -
3、如图所示,将两个正方形并列放置,其中 , , 三点在一条直线上, , , 三点在一条直线上,已知 , , 则阴影部分的面积和是 .

-
4、光从空气射入液体中会发生折射现象.如图,水平放置的容器中装有某种液体,光线斜射到液面发生折射,折射光线为 , 折射角为 , 测得 , , , 则线段的长是 . (结果精确到0.1,参考数据: , , )
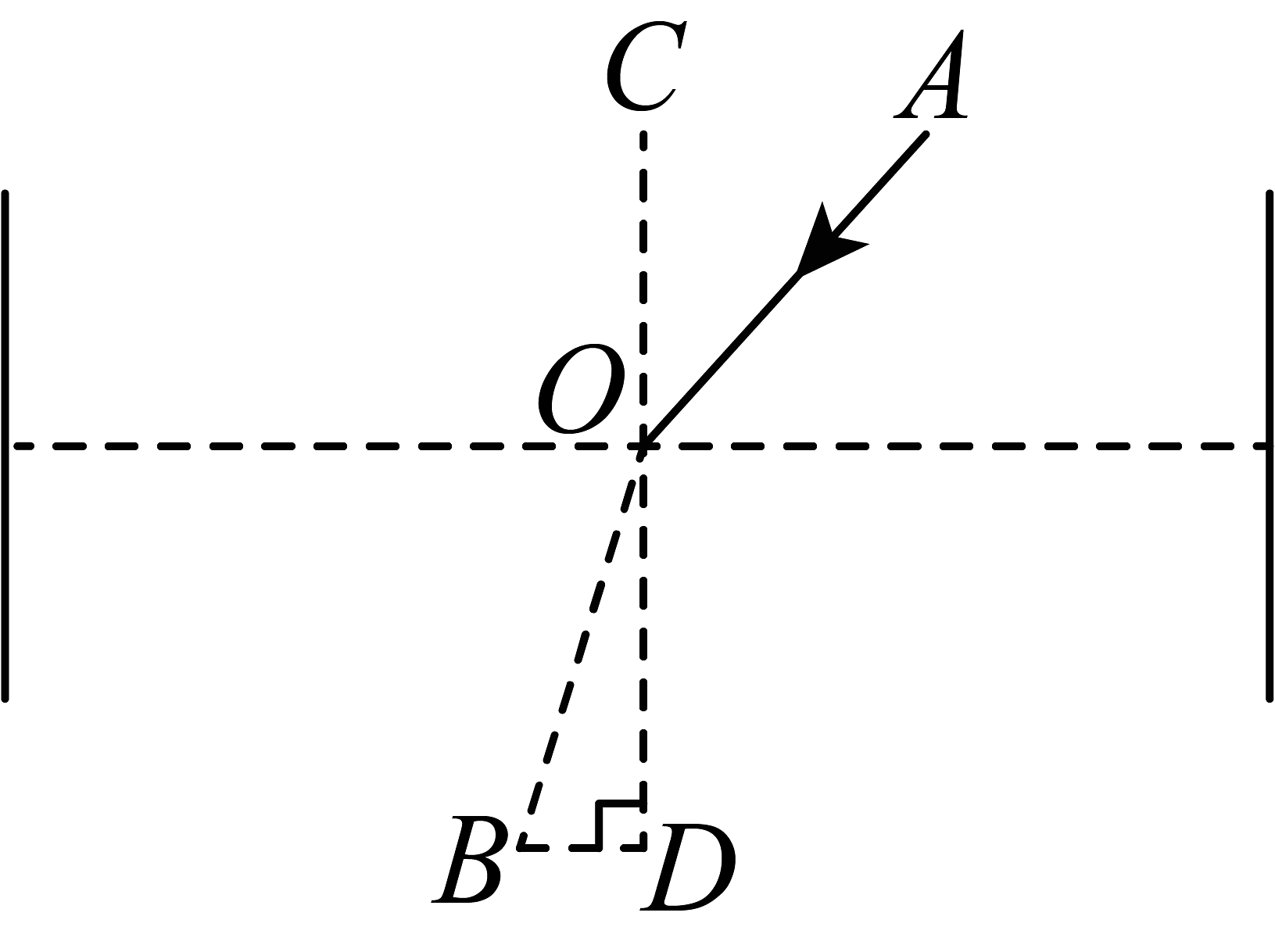
-
5、如图,足球的表面是由12块正五边形的黑皮和20块正六边形的白皮围成的,将足球上的一块黑皮和与它相邻的一块白皮展开放平,则的度数为 .
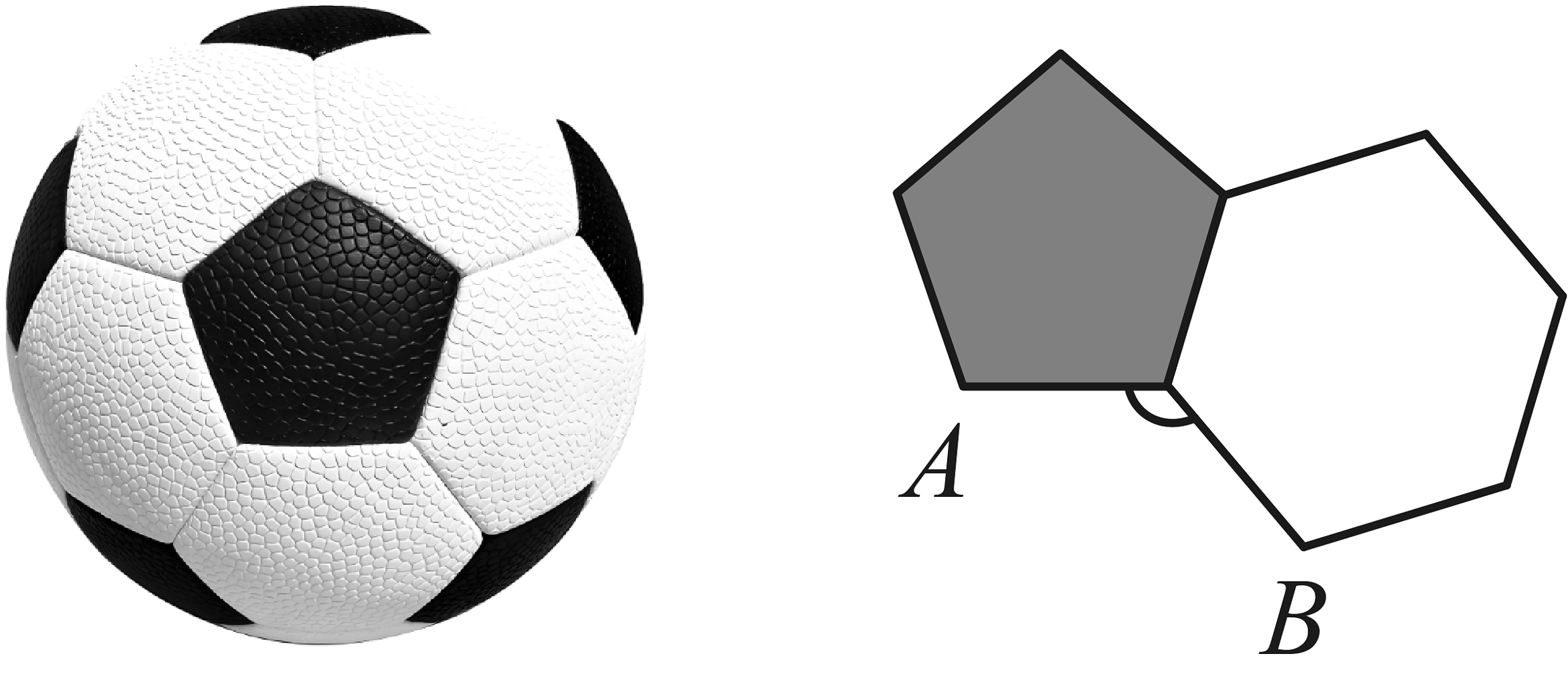
-
6、如图1,《蝶几图》是明朝的戈汕分割正方形的一种方式,以正方形为模分割为长斜(等腰梯形)、右半斜(直角梯形,后同)、左半斜、小三斜(等腰直角三角形,后同)、大三斜和闰(该图内部分割纵向等距).取右半斜两张、左半斜两张、小三斜两张,共6张拼成如图2所示的中心对称图形,并放入一个长方形中,若图1中较大正方形的边长为4,则长方形的周长是( )
 A、15 B、 C、 D、
A、15 B、 C、 D、 -
7、中国是茶的故乡,茶文化是中国制茶和饮茶的文化.某制茶厂购进580克胎菊和1180克枸杞用于制作甲,乙两种袋装茶,其中甲种茶一袋需添加胎菊3克,枸杞5克,乙种茶一袋需添加胎菊2克,枸杞6克.求制茶厂可制作的甲,乙两种茶的袋数.设制茶厂可制作袋甲种茶,袋乙种茶,则可列方程组为( )A、 B、 C、 D、
-
8、小亮设计了一个“配绿色”游戏:如图是两个可以自由转动的转盘,每个转盘被分成面积相等的扇形.游戏者同时转动两个转盘(规定:指针恰好停在分界线上,则重新转一次),如果转盘A指针指向了黄色,转盘B指针指向了蓝色,那么他就赢了,因为黄色和蓝色在一起配成了绿色.这个游戏中游戏者获胜的概率是( )
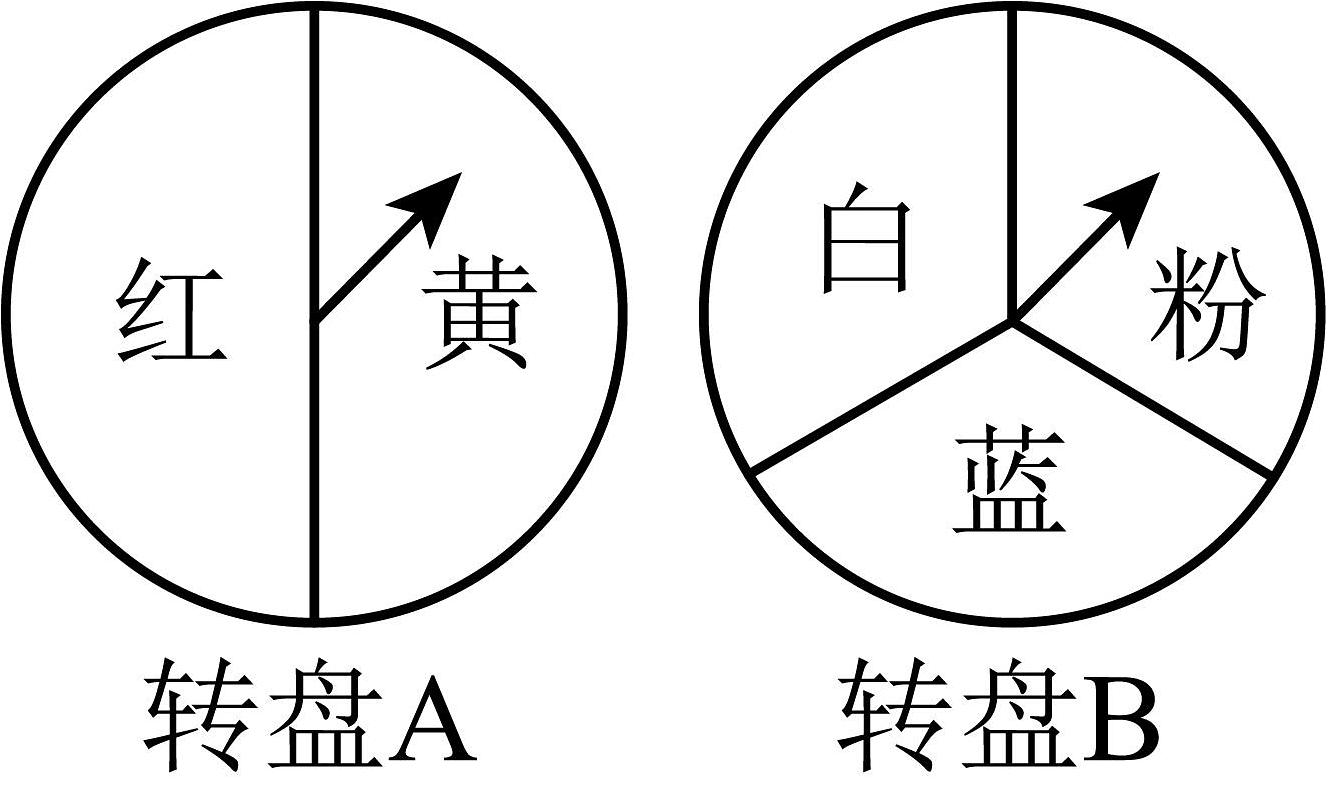 A、 B、 C、 D、
A、 B、 C、 D、 -
9、一款西服上标有下列信息:
洗涤说明
以下网袋机洗,不可漂白,低温熨烫,不可干洗,不可曝晒,请勿浸泡
根据信息,关于这款西服的洗涤温度范围,在数轴上表示正确的是( )
A、 B、
B、 C、
C、 D、
D、
-
10、甲、乙两人10次标枪的落点如图所示,记录成绩(单位:m),则对于甲、乙两人成绩方差 , 的描述正确的是( )
 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定 -
11、如图,在平面直角坐标系中,抛物线与x轴交于点、点 , 与y轴交于点 , 过点B的直线交y轴于点 . 在x轴上方抛物线上有一点P,过点P作的垂线,垂足为E.
 (1)、求抛物线的解析式;(2)、如图1,过点P作x轴的垂线交直线于点Q,当的周长最大时,求此时点P的坐标;(3)、如图2,连接 , 当与相似时,求点E的坐标.
(1)、求抛物线的解析式;(2)、如图1,过点P作x轴的垂线交直线于点Q,当的周长最大时,求此时点P的坐标;(3)、如图2,连接 , 当与相似时,求点E的坐标. -
12、如图,在中, , 点B在上,以为直径的交于点C,连接并延长交于点E,连接、 , 连接交于点F,恰好平分 .
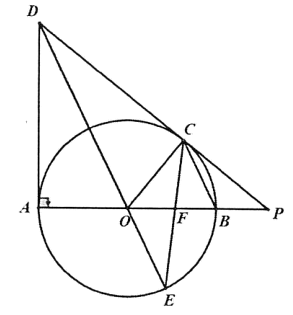 (1)、求证:为的切线;(2)、已知 , , 求的半径和的长.
(1)、求证:为的切线;(2)、已知 , , 求的半径和的长. -
13、如图,在平面直角坐标系下如图放置,其中轴.斜边交x轴于点E,过点A的双曲线交斜边于点B,过点C作双曲线 . , 点A的坐标为 .
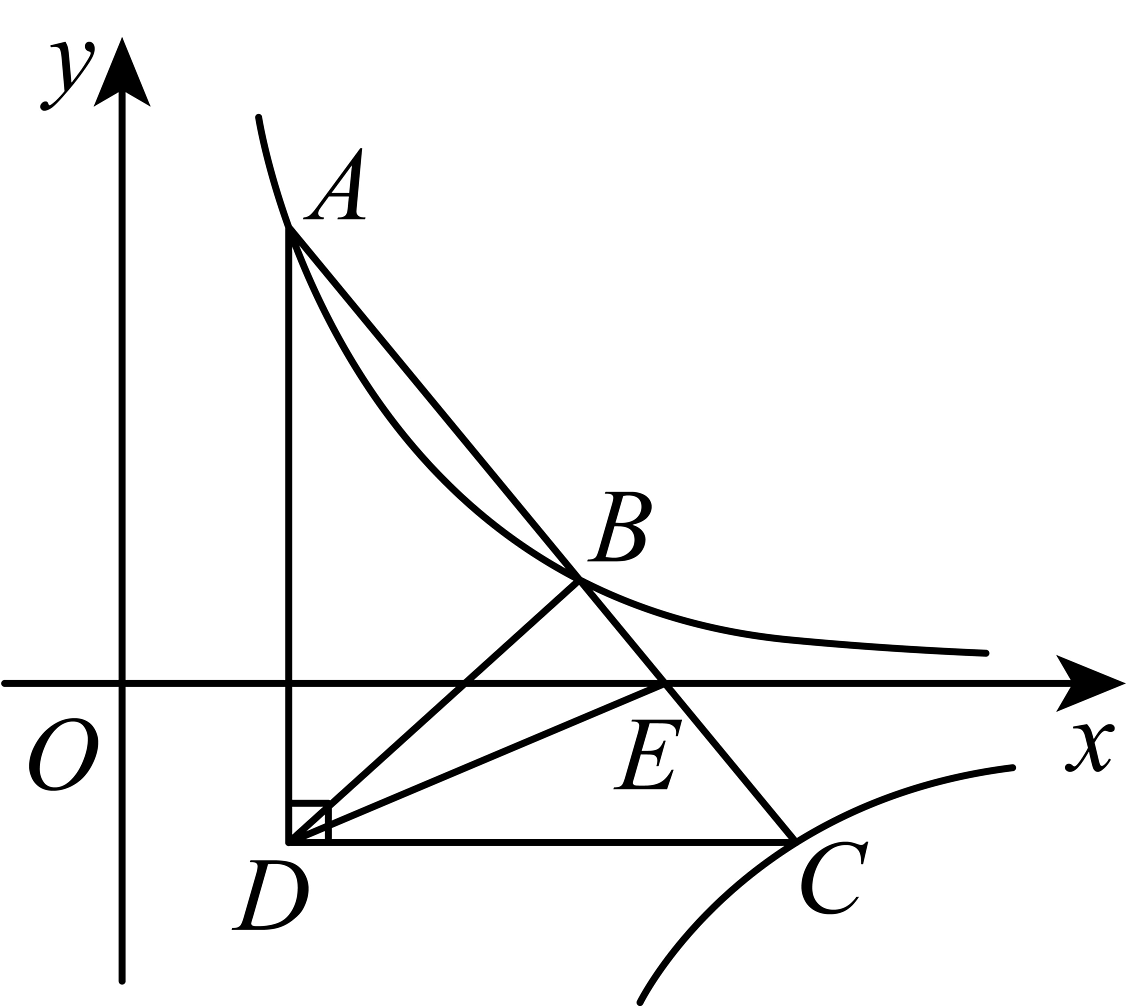 (1)、求直线的解析式与点E的坐标;(2)、连接 , , 当时,求m的值.
(1)、求直线的解析式与点E的坐标;(2)、连接 , , 当时,求m的值. -
14、如图,在矩形中,点E为边上一点,将沿翻折到 , 点B恰好落在边上的点F处.延长、交于点G,连接 , .
 (1)、求证:四边形为菱形;(2)、若 , 且 , 求菱形的面积.
(1)、求证:四边形为菱形;(2)、若 , 且 , 求菱形的面积. -
15、绵阳作为四川省重要的区域中心城市和成渝地区双城经济圈的重要节点,近年来物流业发展迅速,绵阳有望成为川西北物流新高地.现在绵阳某物流公司需要从涪城区运送360吨蔬菜和210吨水果到三台县城,物流公司准备派大货车和小货车共20辆来完成此次运送任务,其每辆车的运载量和运费如下表,
可载蔬菜吨数(吨/辆)
可载水果吨数(吨/辆)
运费(元/辆)
小货车
10
15
500
大货车
20
10
800
设物流公司派小货车x辆,请解决下面的问题:
(1)、求物流公司有哪几种运送方案?(2)、求物流公司采用哪种运送方案使运送费用最低? -
16、近年来绵阳市初中毕业升学体育考试采用“”模式,即3个必考项目和1个选考项目,总分80分,其中跳绳和中长跑由抽签决定考查其中一项.某校为了了解全校学生跳绳项目的成绩水平,学校随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了统计表和统计图(如图).
一分钟跳绳次数的频数表
等级
次数
频数
不合格
4
合格
10
良好
a
优秀
12

请根据上述信息,解答下列问题:
(1)、__________,补全一分钟跳绳次数的频数分布直方图.(2)、若该校有800名学生,估计该校学生一分钟跳绳次数达到合格及以上的人数为__________.(3)、在本次比赛结果为“优秀”等级的学生中,有4位同学一分钟跳绳的次数达190次以上,其中男生和女生各占一半,现准备从这四位同学中选2位参加比赛.请用列表或画树状图的方法,求选出的2位同学恰好性别不同的概率. -
17、(1)计算: ;
(2)化简求值: , 其中满足 .
-
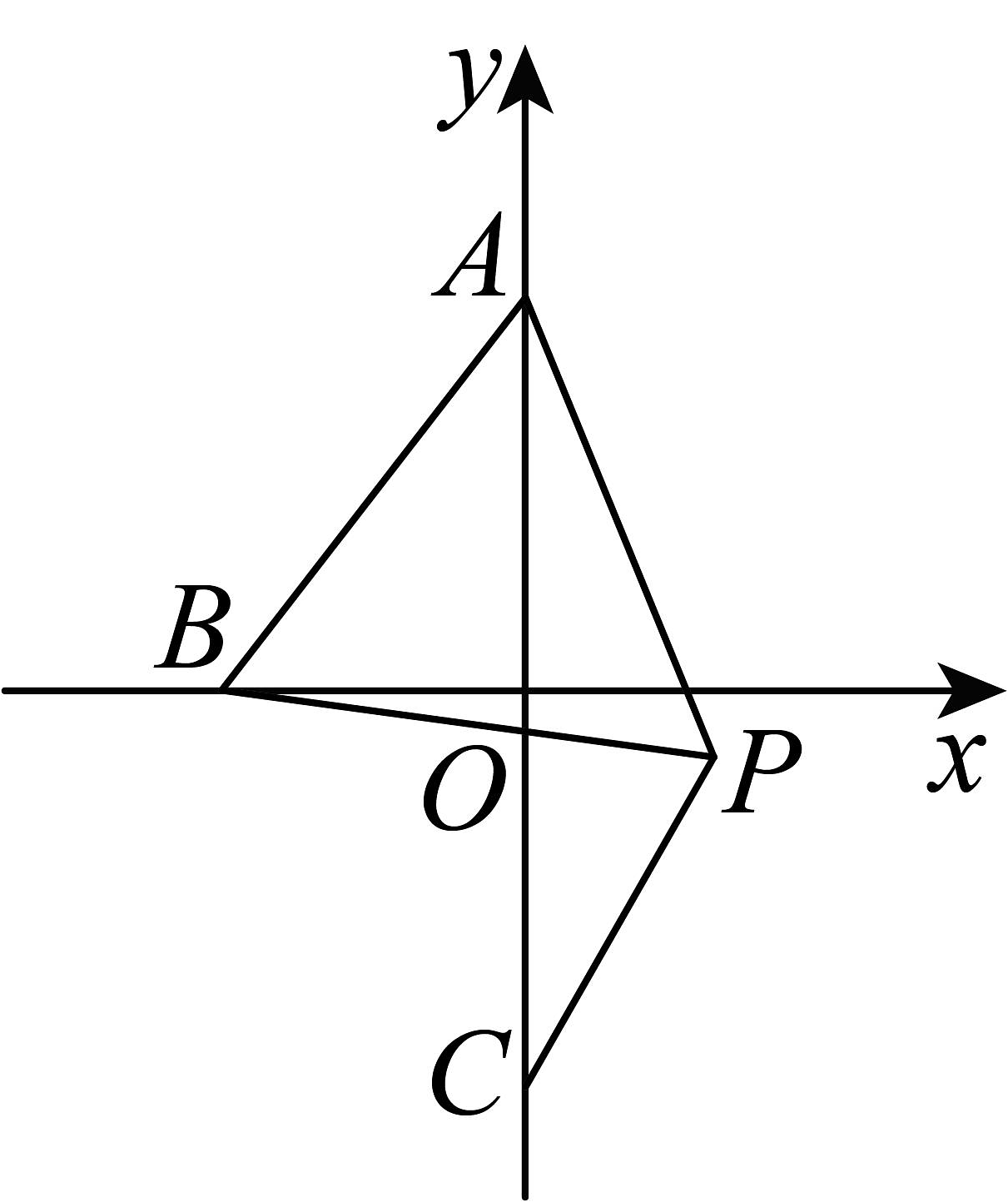
18、如图,在平面直角坐标系中,点A的坐标是 , 点C的坐标是 , 点是x轴上的动点,点B在x轴上移动时,始终保持是等边三角形(点P不在第二象限),连接 , 求得的最小值为 .
-
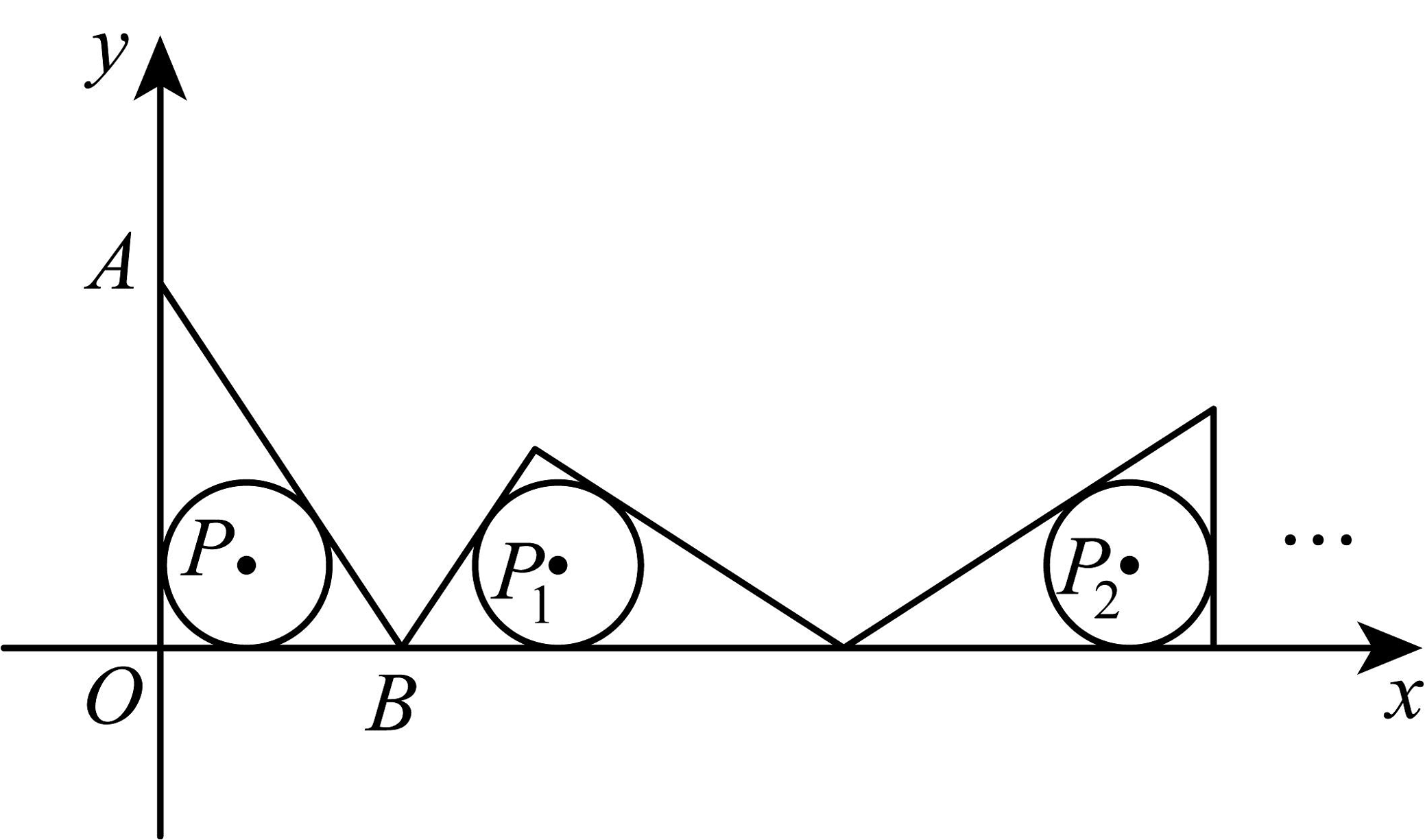
19、如图,把置于平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点P是内切圆的圆心.将沿x轴的正方向作无滑动翻转,使它的三边依次与x轴重合,第一次翻转后圆心为 , 第二次翻转后圆心为 , 依此规律,第21次翻转后,内切圆的圆心的坐标是 .
-
20、若 , 那么x的最小整数值是 .