-
1、由于共享单车的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量逐月增加,据统计,该商城5月份销售自行车64辆,7月份销售100辆.(1)、若该商城5月至7月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.(2)、考虑到自行车需求不断增加,该商场准备再购进一批两种规格的自行车共100辆.已知A型车的进价为每辆500元,售价为每辆700元;B型车的进价为每辆1000元,售价为每辆1300元.假设所购进的车辆全部售完,为使利润不低于26000元,该商场购进A型车不超过多少辆?
-
2、图1是放置在写字台上的一盏折叠式台灯,其主视图如图2,座杆与水平桌面垂直,臂杆可绕点旋转调节,灯体可绕点旋转调节. 若 , , 在同一平面上, , , , 臂杆与座杆的夹角即 , 臂杆与灯体的夹角即 , 灯体上点到水平桌面的高度为 .
 (1)、求的度数.(2)、求的长.(结果精确到 . 参考数据: , , )
(1)、求的度数.(2)、求的长.(结果精确到 . 参考数据: , , ) -
3、某校举行“中国共产党十九大”知识问答竞赛.每班选20名同学参加比赛.根据答对的题目数量得分,等级分为5分,4分,3分,2分.学校将八年级甲班和乙班的成绩整理并绘制成如下的统计图.
甲、乙两班成绩统计表
班级
平均数(分)
中位数(分)
众数(分)
甲班
3.6
4
乙班
3.6
3.5
 (1)、请把甲班知识问答成绩统计图补充完整.(2)、通过统计得到表,请求出表中数据______,______.(3)、根据(2)的结果,你认为甲,乙两班哪个班级成绩更好?写出你的理由.
(1)、请把甲班知识问答成绩统计图补充完整.(2)、通过统计得到表,请求出表中数据______,______.(3)、根据(2)的结果,你认为甲,乙两班哪个班级成绩更好?写出你的理由. -
4、如图,正方形的边在的边上,顶点D、G分别在边、上,如果的边长为20,高为15,那么正方形的边长为 .

-
5、三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上根木条.

-
6、比大且比小的整数是 .
-
7、如图,A,B两点分别为与x轴,y轴的切点. , C为优弧的中点,反比例函数的图像经过点C,则k的值为( )
 A、 B、 C、12 D、16
A、 B、 C、12 D、16 -
8、二次函数的图象过 , , , 四个点,下列说法一定正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
9、下列语句正确的是( )A、负数没有立方根 B、的立方根是 C、立方根等于本身的数只有 D、
-
10、以下是四个银行标志图案,图案中既是中心对称图形又是轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、
-
11、计算的结果等于( )A、 B、 C、 D、
-
12、如图1, 我们把一个半圆和抛物线的一部分围成的封闭图形称为“果圆”, 已知 , , , 分别为“果圆”与坐标轴的交点, 与“果圆”中的抛物线交于 , 两点.
 (1)、求“果圆”中的抛物线的解析式.(2)、“果圆”上是否存在点使?如果存在请求出点的坐标;如果不存在,请说明理由.(3)、如图2,为直线下方“果圆”上一点, 连接 , , , 设与 交于点 , 的面积记为 , 的面积记为 , 求的最小值.
(1)、求“果圆”中的抛物线的解析式.(2)、“果圆”上是否存在点使?如果存在请求出点的坐标;如果不存在,请说明理由.(3)、如图2,为直线下方“果圆”上一点, 连接 , , , 设与 交于点 , 的面积记为 , 的面积记为 , 求的最小值. -
13、如图 , 点为边上的动点(点不与点 , 重合).以点为顶点作 , 射线交边于点 , 过点作交射线于 , 连接 .
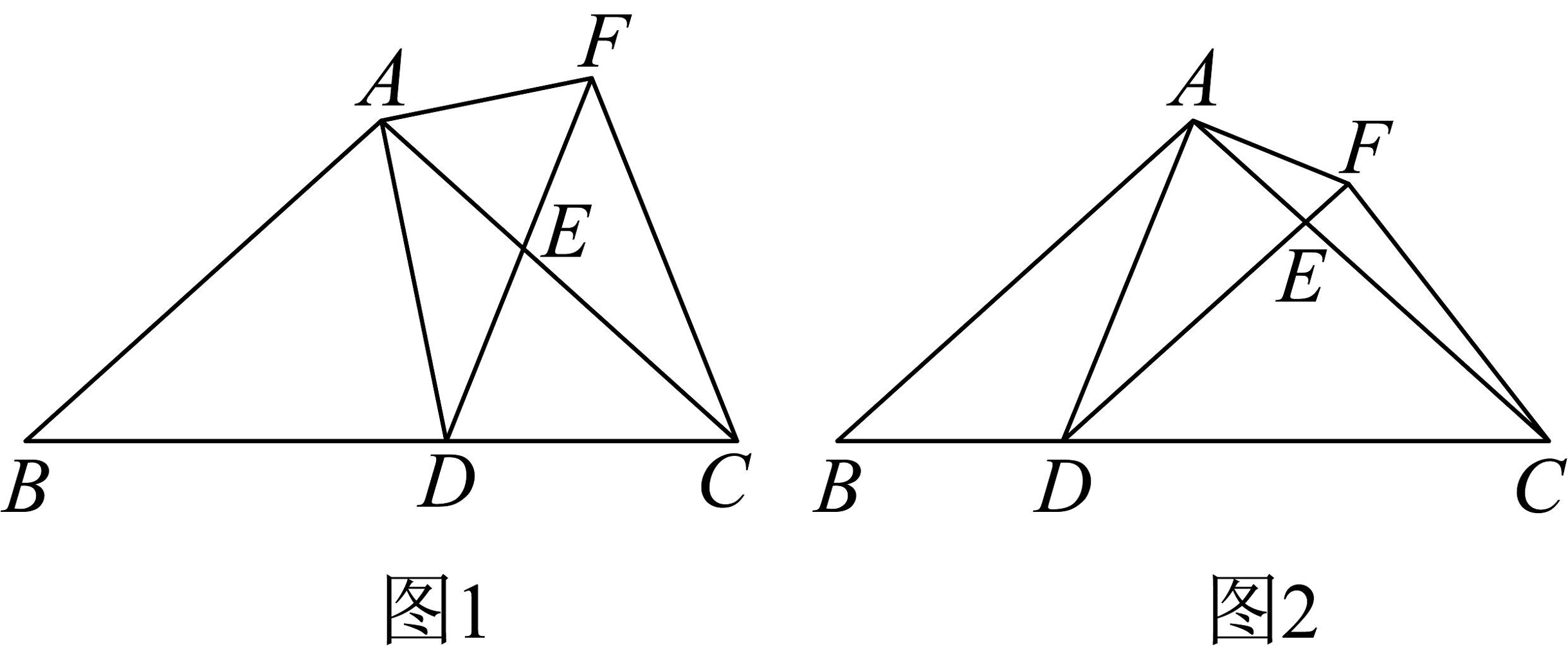 (1)、求证∶ ;(2)、如图2, 当时, 求 的长;(3)、点在边上运动的过程中,是否存在某个位置,使得?若存在,求出此时的长;若不存在,请说明理由.
(1)、求证∶ ;(2)、如图2, 当时, 求 的长;(3)、点在边上运动的过程中,是否存在某个位置,使得?若存在,求出此时的长;若不存在,请说明理由. -
14、无人机在实际生活中应用广泛.如图,小明利用无人机测量大楼的高度,无人机在空中P处测得大楼楼顶D处的俯角为 , 测得楼楼顶A处的俯角为 . 已知楼和楼之间的距离为 , 楼的高度为 , 从楼的A处测得楼的D处的仰角为 . (点A、B、C、D、P在同一平面内)
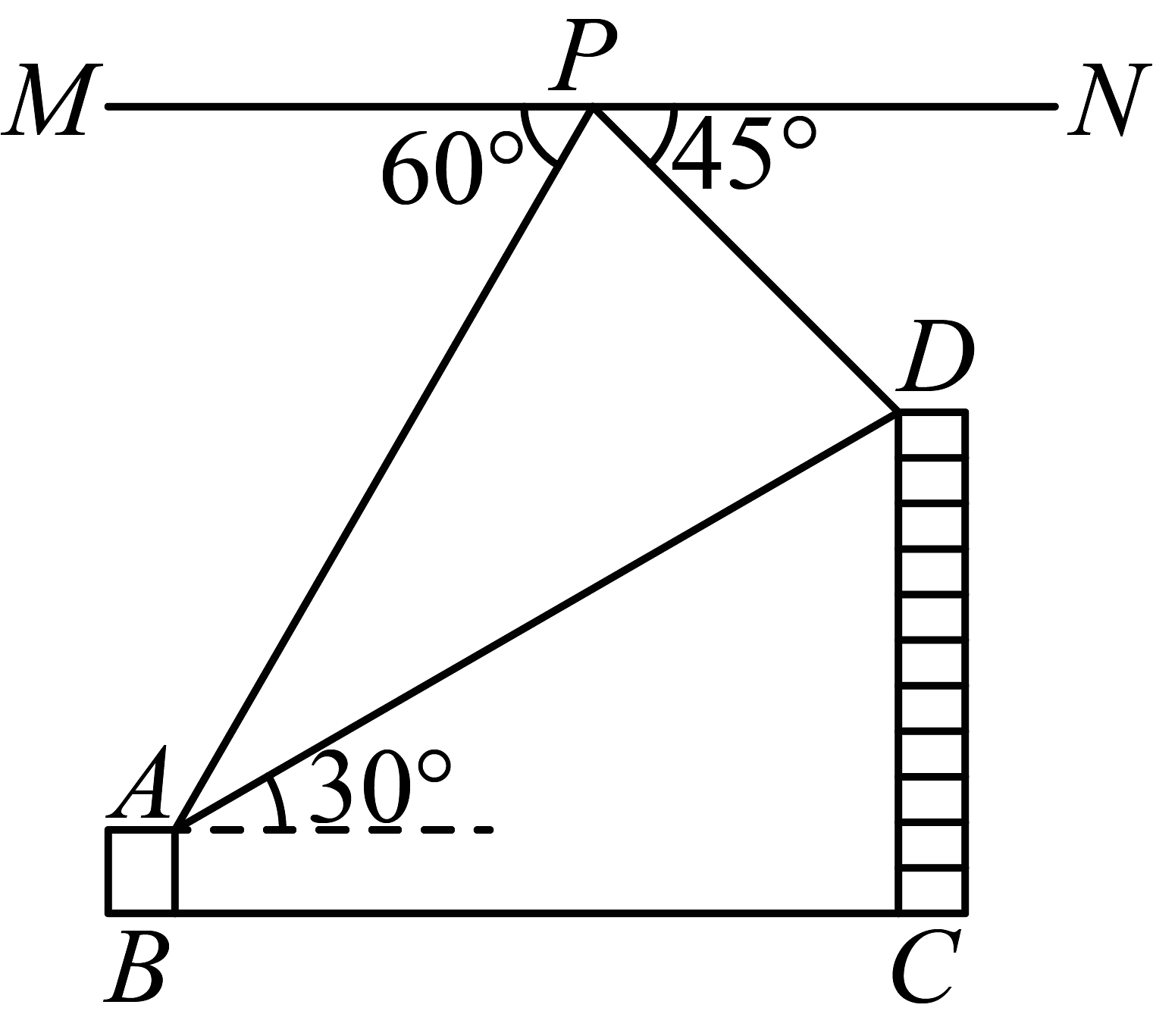 (1)、求楼的高度;(2)、求此时无人机距离地面的高度.(精确到1米,)
(1)、求楼的高度;(2)、求此时无人机距离地面的高度.(精确到1米,) -
15、如图,在平面直角坐标系中,一次函数与反比例函数的图像交于 , 两点,与轴交于点 , 与轴交于点 .
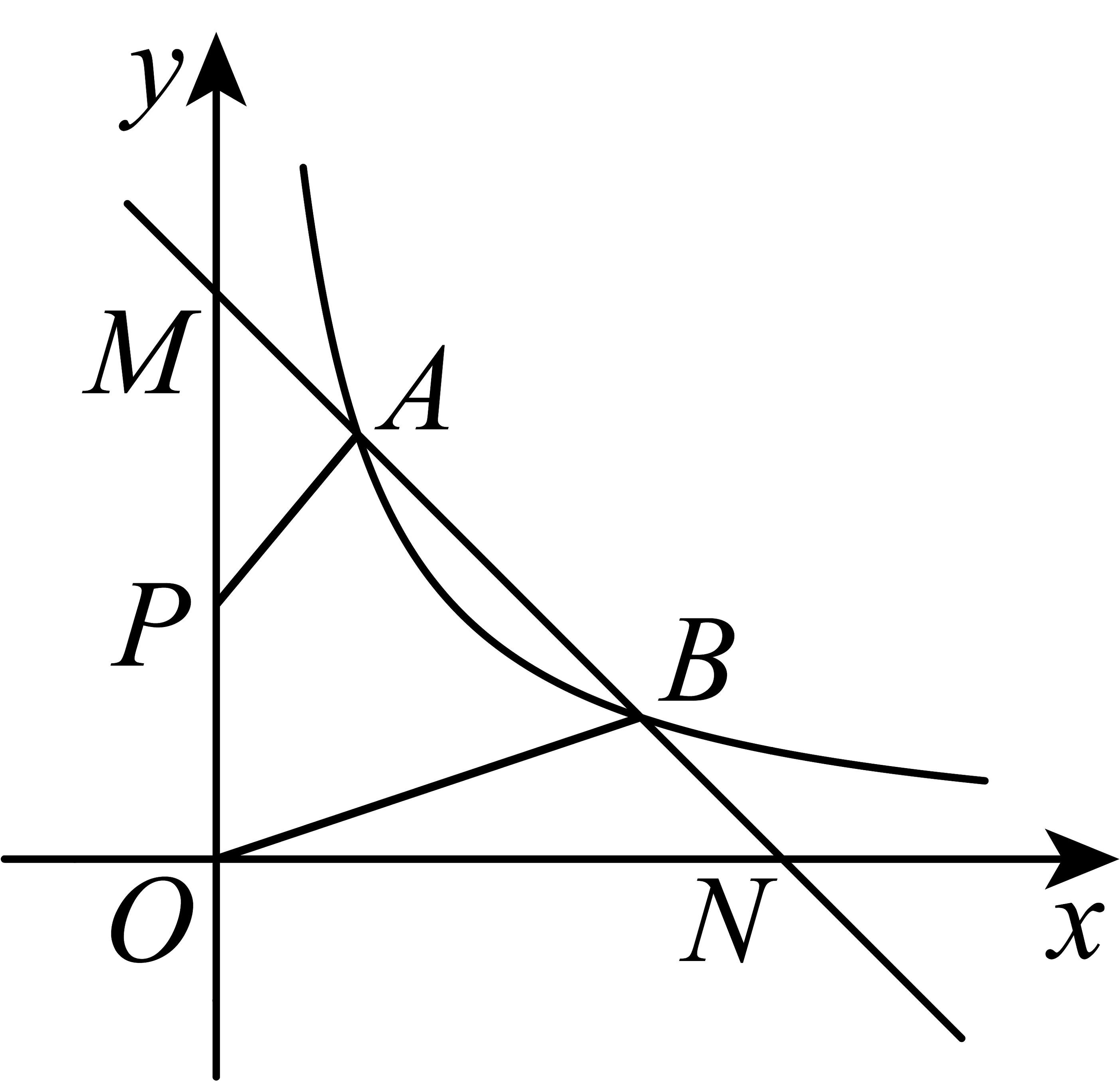 (1)、求直线的解析式;(2)、当时,的取值范围为________;(3)、如图,轴正半轴上有一点 , 连接 , 求四边形的面积.
(1)、求直线的解析式;(2)、当时,的取值范围为________;(3)、如图,轴正半轴上有一点 , 连接 , 求四边形的面积. -
16、某中学在2025年“校园文化艺术节”到来之际,开展了“魅力艺术,和谐校园”主题活动.为此该校在某商场购买了A、B两种奖品,已知购买2个A种奖品和3个B种奖品共花费65元,购买3个A种奖品和6个B种奖品共花费120元.(1)、求购买1个A种奖品和1个B种奖品各需多少元?(2)、该校决定购买A、B两种奖品共50件,其中A种奖品的数量不多于B种奖品数量的 求购买这50件奖品至少花费多少元?
-
17、某学校为丰富教师的业余生活,组织全体教师开展以下体育活动:A.篮球,B.气排球,C.乒乓球,D.羽毛球.为了了解教师最喜欢哪一种活动项目,随机抽取了部分教师进行调查(每位教师必选且只能选择一项),并将调查结果绘制成了如图所示的两幅不完整的统计图.
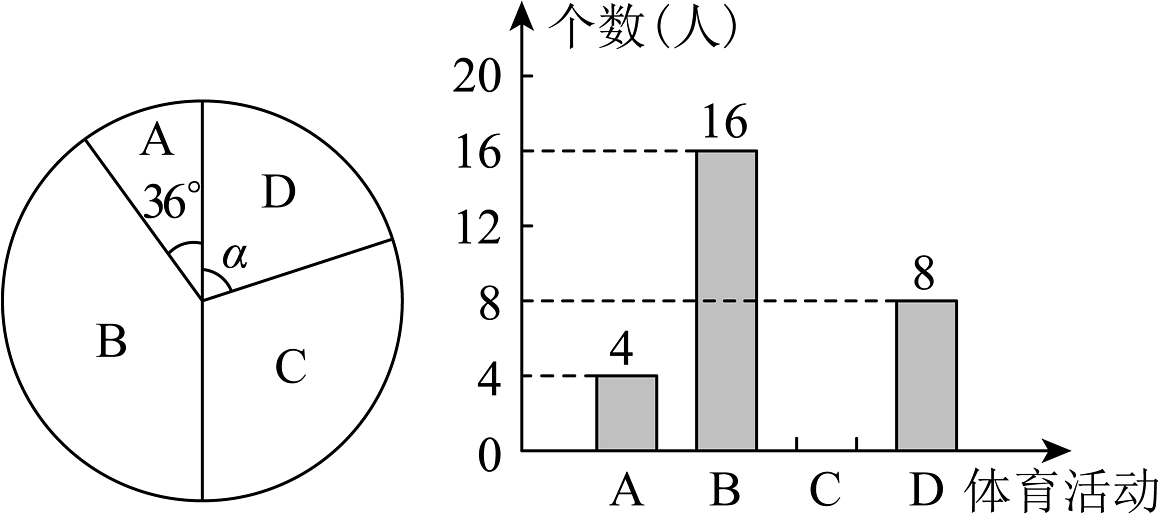
请回答下列问题:
(1)、这次被调查的教师共有 人,在扇形统计图中, “D”对应的扇形圆心角的度数为 ;(2)、请你将条形统计图补充完整;若该校有教师200人,请估计该校喜欢气排球的教师有多少人?(3)、在平时的羽毛球项目练习中,甲、乙、丙、丁四人表现优秀,现决定从这四名教师中任选2人参加羽毛球比赛,请用树状图或列表的方法求恰好选中甲、丙两位教师的概率. -
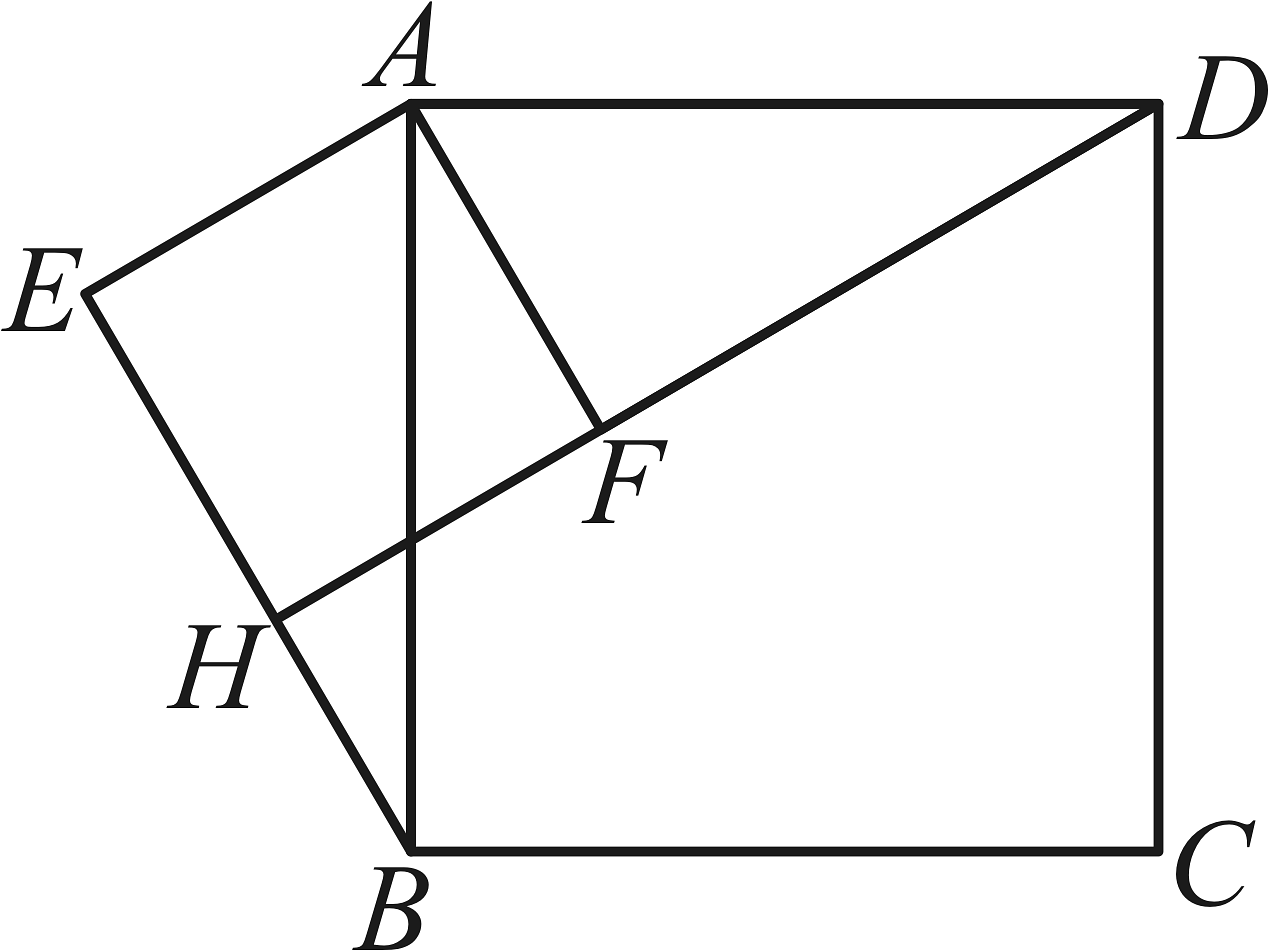
18、如图, 正方形中, , 点E为正方形外一点, 且 将绕点A 逆时针方向旋转得到 , 的延长线交 于点 H. 若 , 则的长为 .
-
19、如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是(结果保留π).

-
20、“”是杭州深度求索人工智能基础技术研究有限公司推出的助手,2025年1月令全球瞩目.某同学随机从中选取一个字母,取得“”的概率是 .