相关试卷

1、已知 $\sqrt{a + 2} + |b - 3| = 0$ ，则 $a + b =$ ．

查看解析
2、古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 $\frac{\sqrt{5} - 1}{2}$ ( $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ，称为黄金比例)，如图，著名的“断臂维纳斯”便是如此，此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是 $\frac{\sqrt{5} - 1}{2}$ ，若某人的身材满足上述两个黄金比例，且头顶至咽喉的长度为 $26 c m$ ，则其身高可能是( )

A、 $165 c m$ B、 $178 c m$ C、 $185 c m$ D、 $190 c m$

查看解析
3、因举办第九届亚冬会，2025年春节期间哈尔滨市累计接待游客约1200万人．将数“1200万”用科学记数法表示为（）

A、 $12 \times 10^{6}$ B、 $0.12 \times 10^{8}$ C、 $1.2 \times 10^{6}$ D、 $1.2 \times 10^{7}$

查看解析
4、如图，某正方体的展开图的每个面上都有一个汉字，则在原正方体中，与“点”字所在面相对的面上的汉字是（）

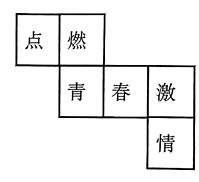A、青 B、春 C、激 D、情

查看解析
5、下列代数运算正确的是（）

A、 ${(x^{3})}^{2} = x^{5}$ B、 ${(2 x)}^{2} = 2 x^{2}$ C、 $x^{3} \cdot x^{2} = x^{5}$ D、

查看解析
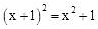
6、为创建文明社区，营造干净整洁的街道社区环境，某社区准备购买甲、乙两种分类垃圾桶，已知购买甲种垃圾桶的单价比购买乙种少50元，用2500元购进乙种垃圾桶的数量是用4000元购进甲种垃圾桶的数量的一半．

(1)、求甲、乙两种垃圾桶的单价；

(2)、该社区拟计划订购这两种垃圾桶共30个，且总费用不超过7000元，则社区最多可以购买多少个乙种垃圾桶？

查看解析
7、某校为了解学生参加家务劳动的情况，对全校学生每周“参加家务劳动的时间”进行了随机抽样调查，并将劳动时间x分为如下四组（A： $x < 60$ ；B： $60 \leq x < 80$ ；C： $80 \leq x < 100$ ；D： $x \geq 100$ ，单位：分钟）进行统计，绘制了如下不完整的统计图．
根据以上信息，回答下列问题：

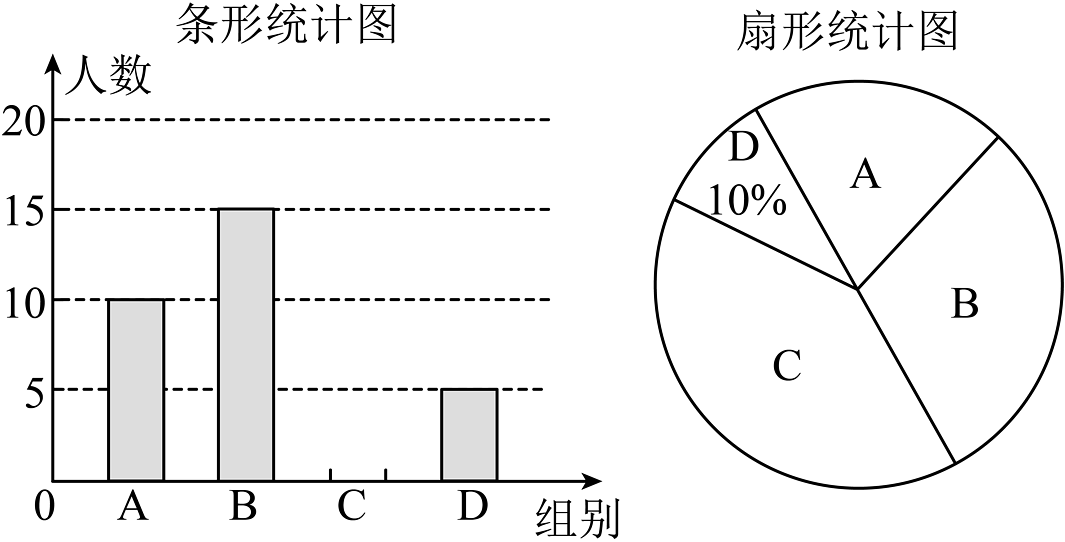(1)、求出本次抽样的学生人数并补全条形统计图；

(2)、已知该校有900名学生，请估计该校学生中每周参加家务劳动的时间不足60分钟的学生有多少人？

(3)、若D组中有2名女生，其余均是男生，从中随机抽取两名同学交流劳动感受，请用列表法或画树状图法，求抽取的两名同学恰好是一名女生和一名男生的概率．

查看解析
8、（1）计算： $(- 9) \div 3 + 3$ ；
（2）解方程组： $\{\begin{array}{l} x + y = 11 \\ 2 x - y = 7 \end{array}$ ．

查看解析
9、在《算法统宗》中有这样一个问题：牧童分杏各争竞，不知人数不知杏．三人五个多十枚，四人八枚两个剩．借问贤能如何算，多少儿童多少杏？问：有几个牧童？题目大意：牧童们要分一堆杏，不知道人数也不知道有多少个杏．若3人一组，每组5个杏，则多10个杏；若4人一组，每组8个杏，则多2个杏．有多少个牧童？设有x个牧童，则可列方程为（）

A、 $4 \times \frac{x - 10}{5} = 3 \times \frac{x - 2}{8}$ B、 $15 x + 10 = 32 x + 2$ C、 $\frac{x}{5} \times 3 - 10 = \frac{x}{8} \times 4 - 2$ D、 $\frac{x}{3} \times 5 + 10 = \frac{x}{4} \times 8 + 2$

查看解析
10、如图，四边形 $A B C D$ 内接于 $⊙ O$ ， $∠ A B C = 135 °$ ， $A C = 2$ ，连接 $O A$ 、 $O C$ ，则 $O A$ 的长为（）

A、4 B、 $2 \sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看解析
11、关于x的一元二次方程 $2 x^{2} - x - k = 0$ 有实数根，则k的取值范围是（）

A、 $k > - \frac{1}{8}$ B、 $k \geq - \frac{1}{8}$ C、 $k \leq - \frac{1}{8}$ D、 $k < - \frac{1}{8}$

查看解析
12、关于正比例函数 $y = - 2 x$ ，下列结论不正确的是（）

A、点 $(1, 2)$ 在函数 $y = - 2 x$ 的图象上 B、y随x的增大而减小 C、图象经过原点 D、图象经过第二、四象限

查看解析
13、下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(- a^{3})}^{2} = a^{6}$ D、 $a^{6} \div a^{3} = a^{2}$

查看解析
14、下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差，根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）
甲
乙
丙
丁
平均数
9.35
9.35
9.34
9.34
方差
6.6
6.9
6.9
6.7

A、甲 B、乙 C、丙 D、丁

查看解析
15、《哪吒之魔童闹海》是一部集剧情、角色塑造、特效以及文化内核于一体的动画电影佳作，它不仅让观众在视听上享受到了极致的体验，更在心灵上获得了深刻的触动和启示．截至2025年3月15日，《哪吒之魔童闹海》全球累计票房（含预售）超150亿元，位列全球影史票房榜第五．将数据15000000000用科学记数法表示为（）

A、 $0.15 \times 10^{11}$ B、 $1.5 \times 10^{10}$ C、 $15 \times 10^{9}$ D、 $1.5 \times 10^{9}$

查看解析
16、如图是“垃圾入桶”标志的平面示意图，若 $∠ 1 = 110 °$ ，则 $∠ B A C$ 的度数是（）

A、 $60 °$ B、 $70 °$ C、 $80 °$ D、 $110 °$

查看解析
17、下列式子是最简二次根式的是（　　）

A、 $\sqrt{9}$ B、 $\sqrt{8}$ C、 $\sqrt{3}$ D、 $\sqrt{\frac{1}{3}}$

查看解析
18、在有理数3， $- 1$ ， $- 3$ ， 0中，最小的数是（）

A、3 B、 $- 1$ C、 $- 3$ D、0

查看解析
19、综合与探究
问题情境：数学活动课上，老师带领同学们以正方形为背景探索几何图形变化中的数学结论．如图1，将边长为4的正方形 $A B C D$ 绕边 $A D$ 的中点O顺时针旋转，得到正方形 $E F G H$ ，点A，B，C，D的对应点分别为点E，F，G，H，直线 $E F$ 与直线 $C D$ 交于点M．
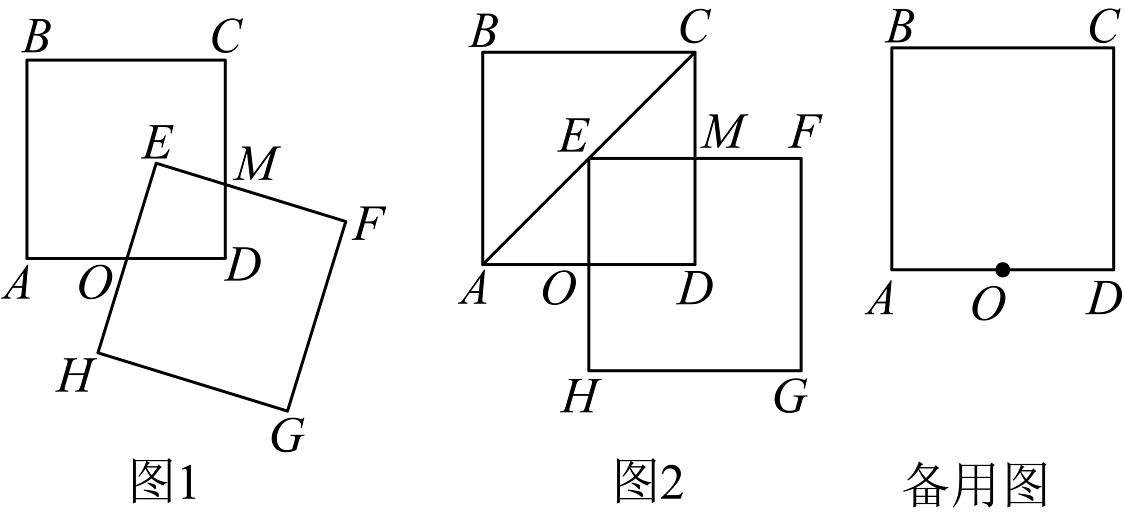
猜想证明：

(1)、如图2，在正方形 $A B C D$ 旋转过程中，当点A的对应点E恰好落在对角线 $A C$ 上时，试判断此时四边形 $O E M D$ 的形状，并说明理由；
深入探究：

(2)、在图1中，猜想线段 $C M$ 与 $M F$ 的数量关系，并说明理由；

(3)、“善思”小组在认真分析正方形旋转到不同位置时的情形后，提出问题：在正方形 $A B C D$ 旋转过程中，当点A，D，F三点共线时，请直接写出线段 $E M$ 的长．

查看解析

20、综合与实践

用硬纸板制作体积最大的无盖纸盒
问题背景	在一次劳动课中，老师准备了一些长为 $40 cm$ ，宽为 $20 cm$ 的长方形硬纸板，准备利用每张纸板制作两个无盖的长方体纸盒（接头处忽略不计）
实践活动	如图，活动小组将纸板在四个直角处裁掉四个边长为 $x cm$ 的正方形，再在中间裁掉一块正方形 $B C F E$ ，再分别沿着虚线折起来，得到两个无盖的长方体纸盒，其中一个纸盒的底面是矩形 $A B C D$
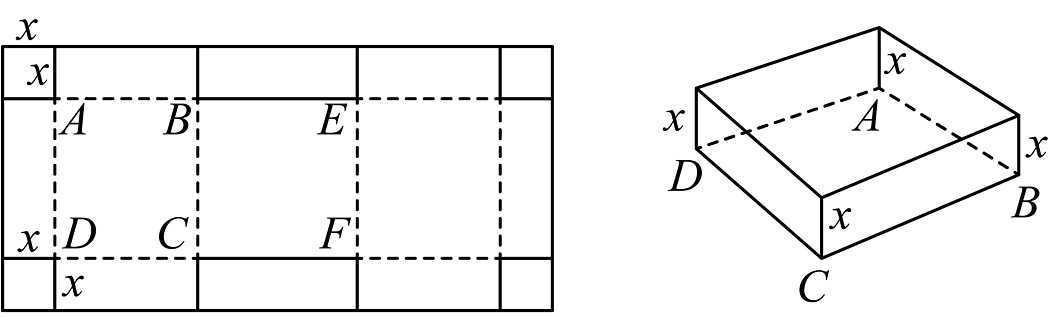
问题解决	（1）求制作的无盖纸盒的底面 $A B$ 边的长．（2）写出一个无盖纸盒的体积 $y ({cm}^{3})$ 与 $x (cm)$ 之间的函数关系式，并求出当x的值为多少时，单个无盖纸盒的体积最大，最大值为多少

查看解析

上一页 327 328 329 330 331 下一页跳转

	甲	乙	丙	丁
平均数	9.35	9.35	9.34	9.34
方差	6.6	6.9	6.9	6.7