相关试卷

1、已知：在平面直角坐标系中，抛物线与 $x$ 轴交于点 $A (1, 0)$ ， $B (3, 0)$ 两点，与 $y$ 轴交于点 $C (0, 3)$ ，

(1)、求抛物线的解析式及顶点 $D$ 的坐标；

(2)、点 $P$ 为抛物线上位于直线 $B C$ 下方的一动点，当 $△ P B C$ 面积最大时，求点 $P$ 的坐标；

(3)、若点 $Q$ 为线段 $O C$ 上的一动点，问： $A Q + \frac{\sqrt{3}}{2} C Q$ 是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

查看解析
2、为适应市场需求，成都博物馆设计了一套全新的“花与器”文创商品，经调查，A、B两种图案的冰箱贴倍受消费者喜爱．已知A种冰箱贴的单价比B种冰箱贴的单价贵10元，用300元购进A种冰箱贴的数量与用200元购买B种冰箱贴的数量相同．

(1)、求A种冰箱贴、B种冰箱贴的单价分别是多少元？

(2)、若某公司购买A、B两种冰箱贴共200个，且A种的数量至少比B种的数量多27个，当购买A、B两种冰箱贴各多少时？总费用最少？并求出最少费用．

查看解析
3、人工智能的应用非常广泛，比如自然语言处理、语音和图象识别、搜索排名、专家系统等．为了解学生对人工智能应用的知晓程度，某校随机抽查部分中学生，进行知识测试，得分用x表示，数据分组为A： $50 \leq x < 60$ 、B： $60 \leq x < 70$ 、C： $70 \leq x < 80$ 、D： $80 \leq x < 90$ 、E： $90 \leq x \leq 100$ ，并将测试成绩绘制成如下不完整的统计图，请根据图表信息回答问题：

(1)、随机抽查的学生共有______人；扇形统计图中“E”组所对应的圆心角度数为______°；

(2)、该校约有7000名学生，请估算等级为C的学生约有多少人？

(3)、在本次调查中，等级为E的学生中，仅有一名男生和三名女生的测试成绩为满分，若从中随机抽取两人进行活动交流，请利用画树状图或列表的方法，求恰好抽到一名男生和一名女生的概率．

查看解析
4、如图，点 $E$ ， $F$ 是正方形 $A B C D$ 的边 $A D$ 上两个动点，满足 $A E = D F$ ．连接 $C F$ 交 $B D$ 于点 $G$ ，连接 $B E$ 交 $A G$ 于点 $H$ ．若正方形 $A B C D$ 的边长为 $2 a$ ，则线段 $D H$ 长度的最小值是．

查看解析
5、国产动画片《哪吒之魔童闹海》火遍全球，目前票房收入达 $155.6$ 亿元，将数据 $155.6$ 亿元用科学记数法表示为元．

查看解析
6、二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图像与 $x$ 轴交于点 $A (- 1, 0)$ ，与 $y$ 轴的交点为 $B$ ，对称轴为直线 $x = 1$ ．下列四个结论：① $3 a + b < 0$ ；②过点 $(0, c - a)$ 平行于 $x$ 轴的直线与抛物线有唯一的公共点；③若 $a > 0$ ，关于 $x$ 的不等式 $a {(x + 1)}^{2} + b (x + 1) < 0$ 的解集为 $- 1 < x < 1$ ；④若 $a < 0$ ，点 $P (t, y_{1})$ ， $Q (t - 1, y_{2})$ 在该抛物线上，当实数 $t < \frac{3}{2}$ 时， $y_{1} > y_{2}$ ．其中正确的结论是（）

A、①②③ B、②③④ C、③④ D、②④

查看解析
7、如图，拦水坝的横断面为梯形 $A B C D$ ， $A F = D E = 6 m$ ，斜面坡度 $i = 1 : 1.5$ 是指坡面的铅直高度 $A F$ 与水平宽度 $B F$ 的比，斜面坡度 $i = 1 : 3$ 是指 $D E$ 与 $C E$ 的比．根据图中数据，求出斜坡 $A B$ 的长为（）

A、13 B、 $3 \sqrt{13}$ C、 $3 \sqrt{11}$ D、11

查看解析
8、学校食堂有10元、11元、12元三种价位的午餐供学生选择（每人购一份），某天午餐销售情况如图所示，则当天学生购买午餐的平均费用是（）

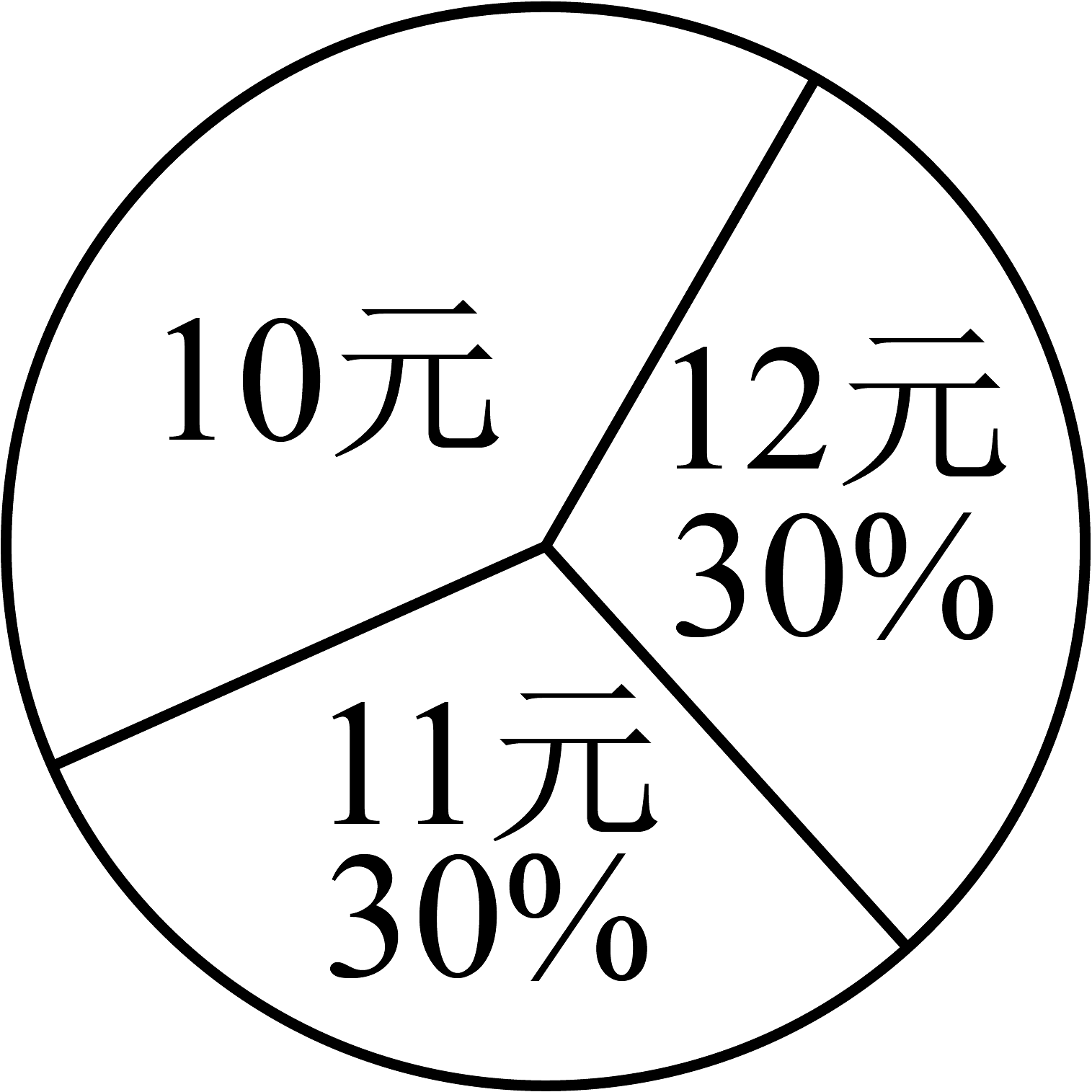A、9.9元 B、10.9元 C、11元 D、11.2元

查看解析
9、中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，如图四幅作品分别代表“立春”“立夏”“芒种”“大雪”，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看解析
10、下列计算不正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ B、 $\sqrt{2^{2} + 3^{2}} = 2 + 3$ C、 $2 \sqrt{2} + 3 \sqrt{2} = 5 \sqrt{2}$ D、 $\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$

查看解析
11、下列各数中最小的数是（）

A、 $- 2$ B、3 C、0 D、 $- 1$

查看解析
12、如图1，在平面直角坐标系中，二次函数 $y = x^{2} + b x + c$ 的图象交 $x$ 轴于 $A (- 1, 0)$ ， $B$ 两点， $A B = 4$ ， $C$ 为抛物线顶点．

(1)、求 $b$ ， $c$ 的值；

(2)、点 $P$ 是抛物线上一动点
①当 $∠ P A D = 45 °$ 时，则点 $P$ 的坐标为______．
②当 $S_{△ A D P} = S_{△ A O D}$ 时，试求点 $P$ 的坐标．

(3)、如图2，以 $B$ 为圆心，2为半径作圆， $N$ 为圆 $B$ 上任一点，求 $C N + \frac{1}{2} A N$ 的最小值．

查看解析
13、【课本再现】
人教版八年级下册数学教材69页有一练习：如图1，四边形 $A B C D$ 是正方形，点 $E$ 是边 $B C$ 的中点， $∠ A E F = 90 °$ ，且 $E F$ 交正方形外角的平分线 $C F$ 于点 $F$ ，求证： $A E = E F$ ．（不需证明，提示：取 $A B$ 的中点 $H$ ，连接 $E H$ ）
【问题提出】
（1）如图2， $E$ 是正方形 $A B C D$ 边 $B C$ 上一点， $△ A E F$ 是等腰三角形， $A E = E F$ ， $∠ A E F = ∠ A B C = 90 °$ ， $A F$ 交 $C D$ 于点 $G$ ，求证： $∠ G C F = 45 °$
【问题探究】
（2）如图3，若 $E$ 是菱形 $A B C D$ 边 $B C$ 上一点， $△ A E F$ 是等腰三角形， $A E = E F$ ， $∠ A E F = ∠ A B C = α (α \geq 90 °)$ ， $A F$ 交 $C D$ 于点 $G$
①当 $α = 100 °$ 时， $∠ G C F =$ _____；
②求 $∠ G C F$ 与 $α$ 的数量关系．
【问题拓展】
（3）如图4，在（2）的条件下，当 $α = 120 °$ 时，若 $\frac{D G}{C G} = \frac{1}{2}$ ，求 $\frac{B E}{C E}$ 的值．

查看解析
14、为落实中央“双减”精神，某校拟开设四门校本课程供学生选择：A．文学鉴赏，B．越味数学，C．川行历史，D．航模科技．为了解该校八年级1000名学生对四门校本课程的选择意向，张老师做了以下工作：①抽取40名学生作为调查对象；②整理数据并绘制统计图；③收集40名学生对四门课程的选择意向的相关数据：④结合统计图分析数据并得出结论．

(1)、请对张老师的工作步骤正确排序______．

(2)、以上步骤中抽取40名学生最合适的方式是______．
A．随机抽取八年级三班的40名学生 B．随机抽取八年级40名男生
C．随机抽取八年级40名女生 D．随机抽取八年级40名学生

(3)、如图是张老师绘制的40名学生所选课后服务类型的条形统计图，假设全年级每位学生都做出了选择，且只选择了一门课程．若学校规定每个班级不超过40人，请你根据图表信息，估计该校八年级至少应该开设几个趣味数学班．

查看解析
15、如图，四边形 $A B C D$ 为正方形， $E$ 为 $C D$ 上一点， $B F ⊥ A E$ 于点 $F$ ，连接 $D F$ ，设 $∠ A B F = α$ ，若 $B F = 2 A F$ ，则 $∠ A D F =$ ．（用含 $α$ 的式子表示）

查看解析
16、已知一个正 $n$ 边形的每个内角都为 $120 °$ ，则 $n =$ ．

查看解析
17、如图，已知平行四边形 $A O B C$ 的顶点 $O (0, 0)$ ， $B (4, 0)$ ， $C (5, \sqrt{3})$ ， $∠ A O B = 60 °$ ，点 $B$ 在 $x$ 轴正半轴上，按以下步骤作图：①分别以点 $O$ ， $A$ 为圆心，以大于 $\frac{1}{2} O A$ 的长为半径画弧，两弧相交于点 $M$ ， $N$ ；②连接 $M N$ ，交 $A O$ 于点 $E$ ，交 $x$ 轴于点 $F$ ，则点 $F$ 的坐标为（）

A、 $(1, 0)$ B、 $(2, 0)$ C、 $(\sqrt{3}, 0)$ D、 $(\frac{3 \sqrt{3}}{2}, 0)$

查看解析
18、若点 $(- 2, y_{1}), (1, y_{2}), (3, y_{3})$ 在反比例函数 $y = \frac{\sqrt{3}}{x}$ 的图象上，则 $y_{1}, y_{2}, y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{1} < y_{3} < y_{2}$

查看解析
19、截至 $2025$ 年 $3$ 月 $28$ 日，《哪吒之魔童闹海》总票房（含预售）达 $153.91$ 亿元，不仅仅是中国影史上首部破百亿大关的电影，更创造全球动画影史的新纪录，国漫崛起势不可挡．数据 $153.91$ 亿用科学记数法表示为（）

A、 $1.5391 \times 10^{11}$ B、 $1.5391 \times 10^{10}$ C、 $15.391 \times 10^{10}$ D、 $0.15391 \times 10^{11}$

查看解析
20、【知识技能】
（1）如图1，在矩形 $A B C D$ 中，点E，F分别在边 $D C$ ， $B C$ 上， $A E ⊥ D F$ ，垂足为点G．求证： $△ A D E ∽ △ D C F$ ．
【数学理解】
（2）如图2，在正方形 $A B C D$ 中，点E，F分别在边 $D C$ ， $B C$ 上， $A E = D F$ ，延长 $B C$ 到点H，使 $C H = D E$ ，连接 $D H$ ．求证： $∠ A D F = ∠ H$ ．
【拓展探案】
（3）如图3，在菱形 $A B C D$ 中，点E，F分别在边 $D C$ ， $B C$ 上， $A E = D F = 10$ ， $D E = 7$ ， $∠ A E D = 60 °$ ，求 $C F$ 的长．

查看解析

上一页 325 326 327 328 329 下一页跳转