-
1、在平面直角坐标系中,点在轴运动,点在轴上运动,满足 . 点为线段的中点,则点运动路径的长为 .
-
2、若 , , 则代数式的值为 .
-
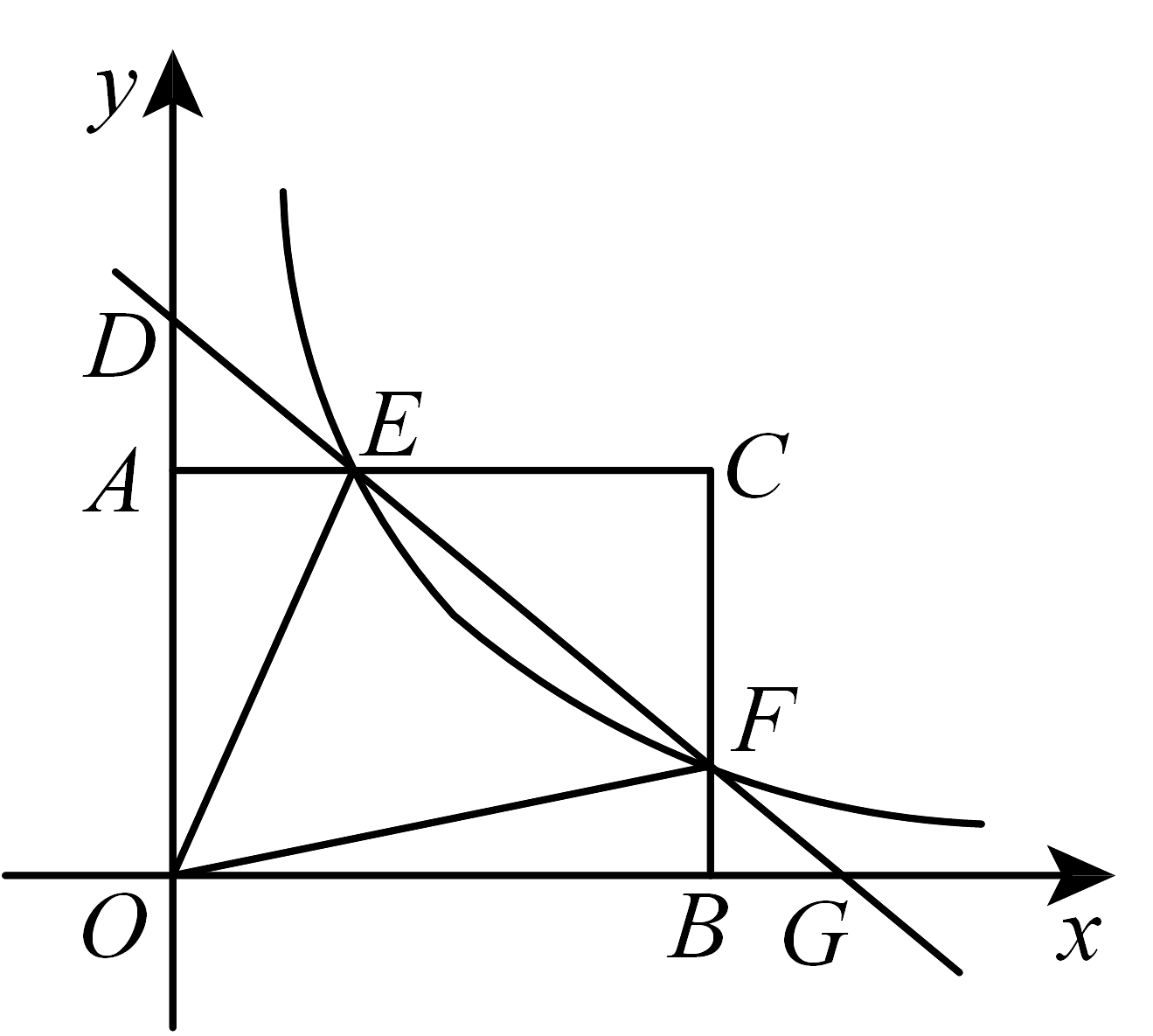
3、如图,矩形的边 , , 动点F在边上(不与B、C重合),过点F的反比例函数的图象与边交于点E,直线分别与y轴和x轴相交于点D和G.给出下列命题:
①若 , 则的面积为;
②若 , 则点C关于直线的对称点在x轴上;
③满足题设的k的取值范围是;
④若 , 则;
⑤连接 , 则直线 .
其中正确的命题个数是( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
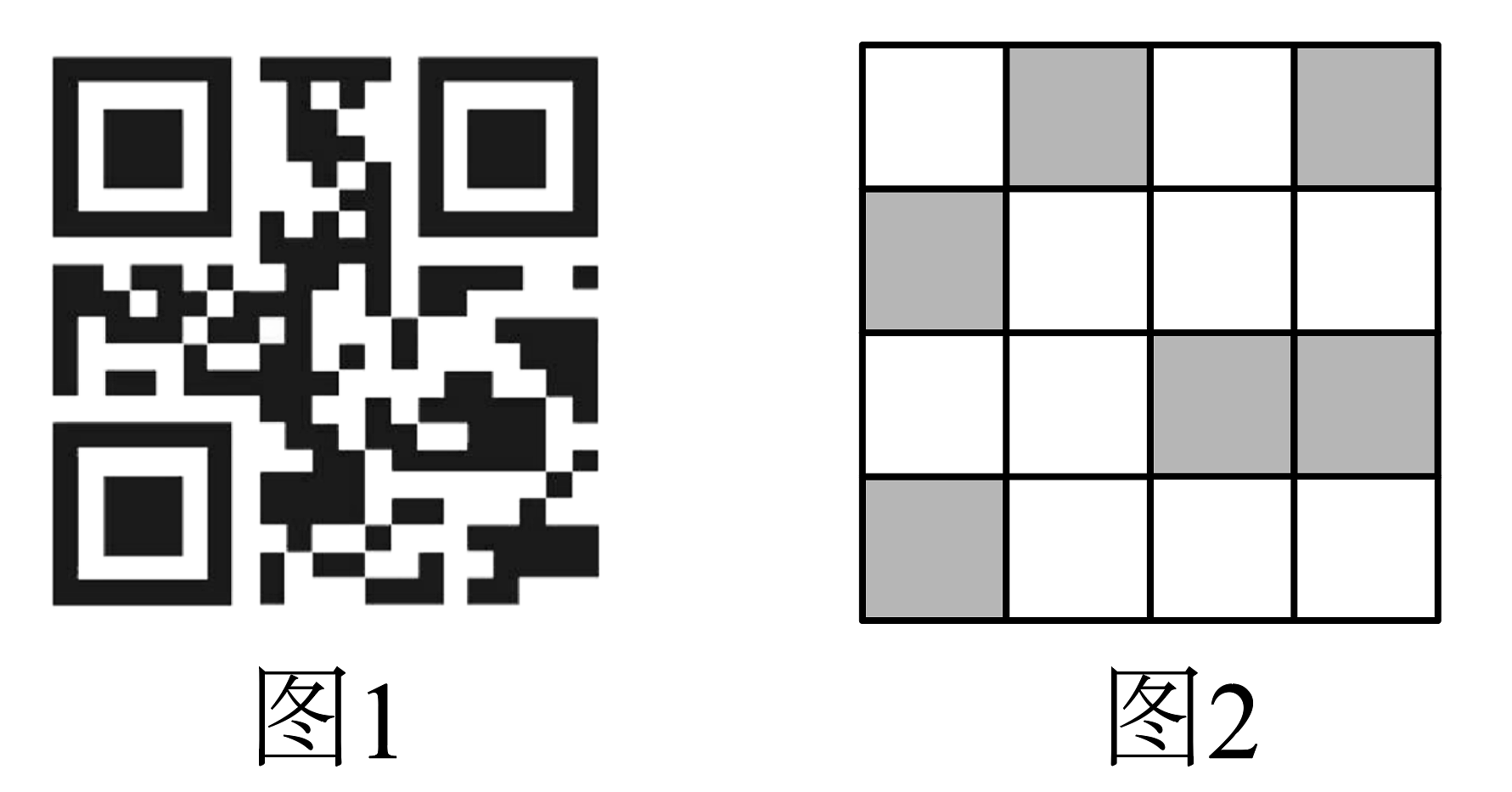
4、利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为 , 如图2第一行数字从左到右依次为0,1,0,1,序号为 , 表示该生为5班学生.那么表示9班学生的识别图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
5、骑行单车这种“低碳”出行方式已融入人们的日常生活,如图是某单车车架的示意图,线段 , , 分别为前叉、下管和立管(点C在上),为后下叉.已知 , , , , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、下列各式计算正确的是( )A、 B、 C、 D、
-
7、深度求索是一家专注于研究世界领先的通用人工智能底层模型与技术、挑战人工智能前沿性难题的创新型科技公司,的芯片在每秒可以处理数据的同时,执行580万亿次浮点运算,数据580万亿可用科学记数法表示为( )A、 B、 C、 D、
-
8、有下列命题:①两直线平行,同位角相等;②垂线段最短;③同角的余角相等;④同旁内角互补;⑤两点确定一条直线.其中假命题是(填序号).
-
9、问题情境
在等边△ABC的两边AB,AC上分别有两点M,N,点D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.

特例探究
如图1,当DM=DN时,
(1)∠MDB= 度;
(2)MN与BM,NC之间的数量关系为 ;
归纳证明
(3)如图2,当DM≠DN时,在NC的延长线上取点E,使CE=BM,连接DE,猜想MN与BM,NC之间的数量关系,并加以证明.
拓展应用
(4)△AMN的周长与△ABC的周长的比为 .
-
10、阅读材料:利用公式法,可以将一些形如的多项式变形为的形式,我们把这样的变形方法叫做多项式的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如: .
例如:求代数式的最小值.
原式 .
,
当时,有最小值是2.
根据以上材料,解答下列问题.
(1)、分解因式(利用配方法):;(2)、求多项式的最小值;(3)、已知a,b,c是的三边长,且满足 , 求的周长. -
11、如图,中, , 将沿着一条直线折叠后,使点与点重合(图②).
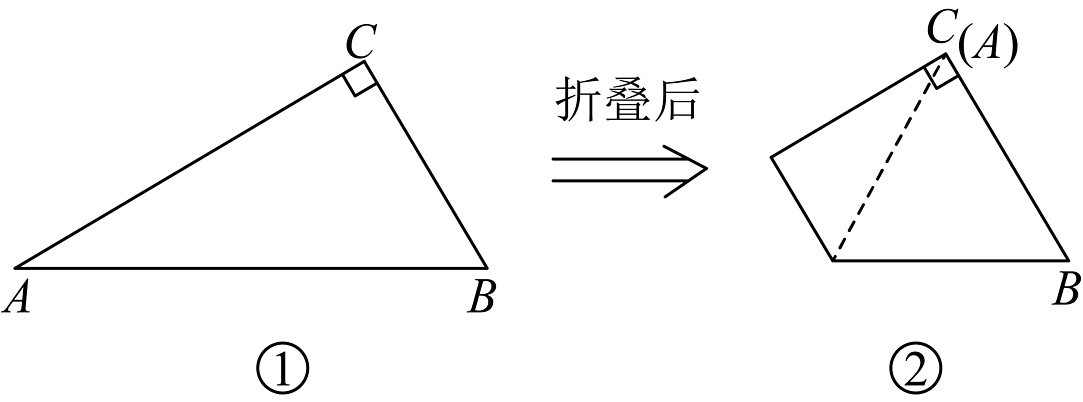 (1)、在图①中画出折痕所在的直线 . 直线与分别相交于点 , 连结(尺规作图,保留作图痕迹).(2)、在(1)的条件下,证明:是等腰三角形.
(1)、在图①中画出折痕所在的直线 . 直线与分别相交于点 , 连结(尺规作图,保留作图痕迹).(2)、在(1)的条件下,证明:是等腰三角形. -
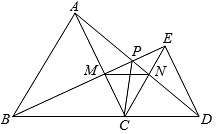
12、如图,和都是等边三角形,、、三点在一条直线上,与相交于点 , 、相交于点 , 、相交于点 , 则下列五个结论:①;②;③;④平分;⑤是等边三角形.⑥MN∥BD.其中,一定正确的有( )
 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个 -
13、若、的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、
-
14、在中, , , , 点是线段上的一个动点,以为直径作圆 .
 (1)、当时,如图1,求证:圆与相切;(2)、如图2,连接 , 与圆相交于点 , 连接 , 请你求出的最小值并说明理由;(3)、如图3, , 若点是圆上的一个动点,且点在内,连接、 , 请你直接写出的最小值.
(1)、当时,如图1,求证:圆与相切;(2)、如图2,连接 , 与圆相交于点 , 连接 , 请你求出的最小值并说明理由;(3)、如图3, , 若点是圆上的一个动点,且点在内,连接、 , 请你直接写出的最小值. -
15、数学活动课上,同学们在刘老师的指导下对二次函数进行了研究.(1)、甲同学经过分析后发现,无论取任何实数,该函数的图象与轴都有两个交点.请你通过计算判断甲同学的说法是否正确.(2)、刘老师为了让同学们更好地感悟“数形结合”的思想,提出了新问题:若该函数图象经过点 , 当时,求的取值范围.
乙同学经过思考后,通过待定系数法求函数的解析式,利用函数的图象与性质确定了的最大值和最小值,进而求出的取值范围.请你结合自己对二次函数的理解求出的取值范围.
(3)、刘老师要求同学们能对所学知识举一反三,进一步研究:在已知(2)的函数解析式的前提下,若 , 且函数的最大值和最小值之差为6,求的值. -
16、若一元二次方程( , , 是常数,且)的两根分别是 , , 根据求根公式可以推出 , .(1)、运用:若一元二次方程的两根分别是 , , 则 .(2)、类比探究:小芳同学发现 .
请你试证明: .
(3)、若 , 是关于的方程的两个实数根,且 , 求的值. -
17、如图,一辆卡车使用一条不可伸缩的长绳通过岸边的定滑轮向左牵引小船靠岸,已知长绳段与水面平行,且岸边 , 当长绳段与水平方向的夹角时,船头离岸边的距离为米,已知甲板始终保持与水面平行,且到水面的距离为0.65米.
 (1)、求定滑轮到水面的距离 .(2)、当小船受长绳牵引,船头前进到点处,此时长绳段与水平方向的夹角 , 求卡车向左移动了多少米?(结果精确到0.1米.参考数据: , , )
(1)、求定滑轮到水面的距离 .(2)、当小船受长绳牵引,船头前进到点处,此时长绳段与水平方向的夹角 , 求卡车向左移动了多少米?(结果精确到0.1米.参考数据: , , ) -
18、某校在推进新课程改革的过程中,自主开发了五门校本课程,分别是: . 人工智能探索; . 传统文化寻根; . 体质与健康; . 山歌唱四方; . 书香润心.每名同学根据自己的爱好只能选择其中一门课程,学校对全校同学的选课情况进行了随机抽样调查,制成了如图所示的两幅不完整的统计图.
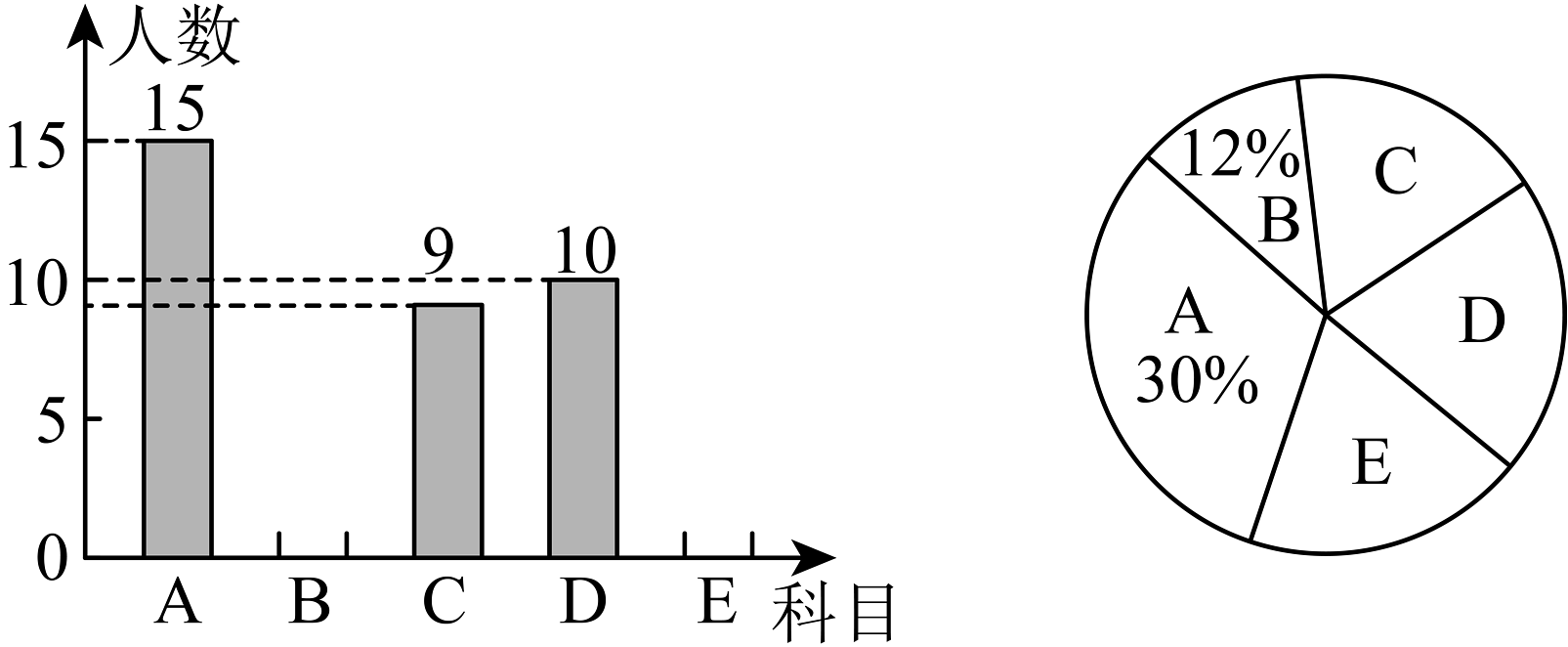 (1)、补全条形统计图,课程所在的扇形的圆心角的度数是____;(2)、若该校有名学生,请你估计该校选择课程的学生有多少名?(3)、某班有名同学,其中名同学选择课程 , 名同学选择课程 , 名同学选择课程 . 若从这名同学中随机抽取名同学,请你用列表法或画树状图的方法求抽取的这名同学都是选择课程的概率.
(1)、补全条形统计图,课程所在的扇形的圆心角的度数是____;(2)、若该校有名学生,请你估计该校选择课程的学生有多少名?(3)、某班有名同学,其中名同学选择课程 , 名同学选择课程 , 名同学选择课程 . 若从这名同学中随机抽取名同学,请你用列表法或画树状图的方法求抽取的这名同学都是选择课程的概率. -
19、如图,四边形是平行四边形,是边上的一点,且 .
 (1)、尺规作图:作的平分线 , 交于点(不写作法,保留作图痕迹).(2)、连接 . 求证:四边形是菱形.
(1)、尺规作图:作的平分线 , 交于点(不写作法,保留作图痕迹).(2)、连接 . 求证:四边形是菱形. -
20、(1)计算;
(2)解方程组: .