-
1、用数轴解不等式组 .

-
2、计算: .
-
3、如图,在正方形中,点、分别在边、上,且 , 点关于直线的对称点在线段的延长线上,与交于点 .
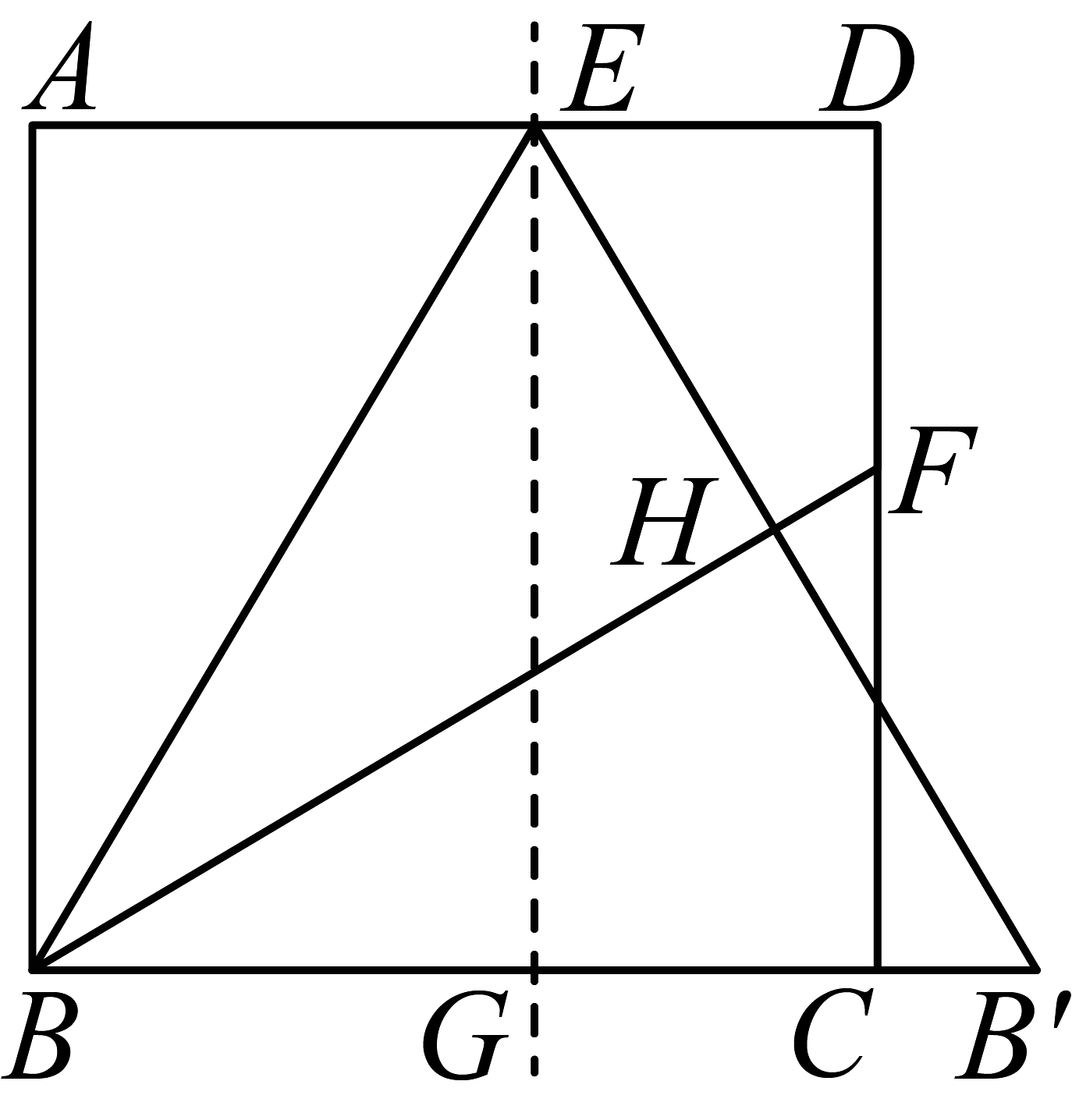
(1)若点与点关于直线对称,则;
(2)若 , 则 .
-
4、把电阻值分别为的两电阻并联后接入某电路中,其并联总电阻值(单位:)满足 . 当时, .
-
5、如图,在中, , 是边上的中线,点到的距离为2,则 .

-
6、因式分解: .
-
7、如图,在矩形中, , , 点为对角线的中点,为线段上一点,连结 , 并延长交于点 , 以点为圆心,适当长为半径画弧,交于点 , 交于点 . 再以点为圆心,长为半径画弧,两弧交于点 , 连接 , 并延长交线段于点 . 则下列两个命题中说法正确的是( )
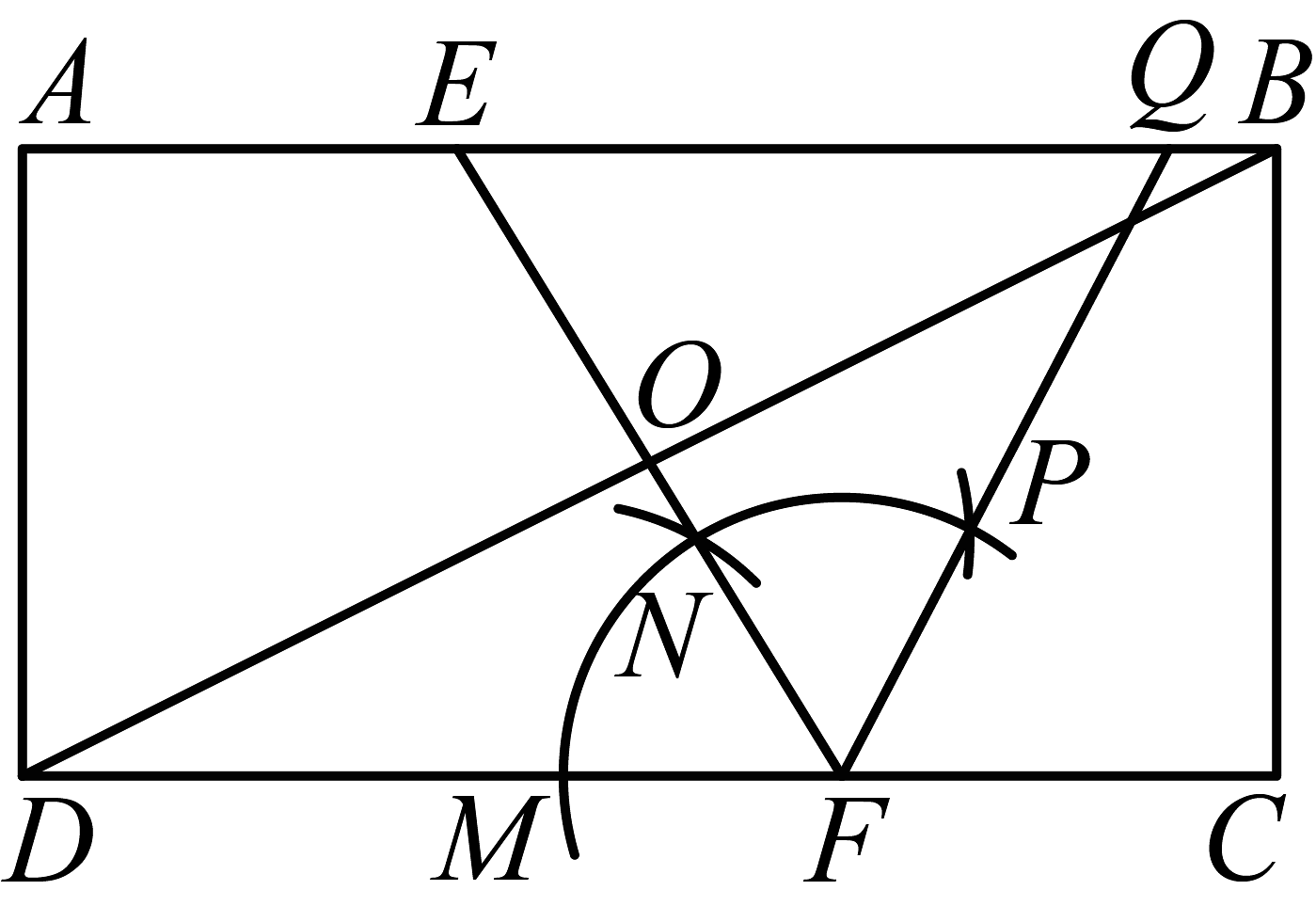
为等腰三角形;
设长为 , 长为 , 则 .
A、正确,正确 B、正确,错误 C、错误,正确 D、错误,错误 -
8、已知某函数的函数值和自变量的部分对应值如下表:
. ..
. ..
. ..
. ..
则这个函数的图象可能是( )
A、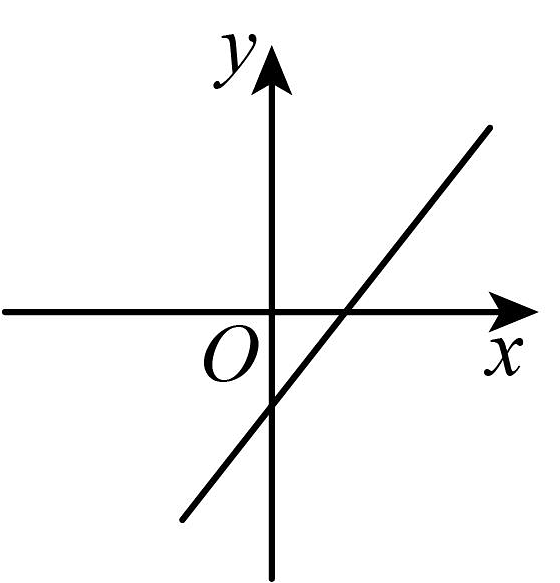 B、
B、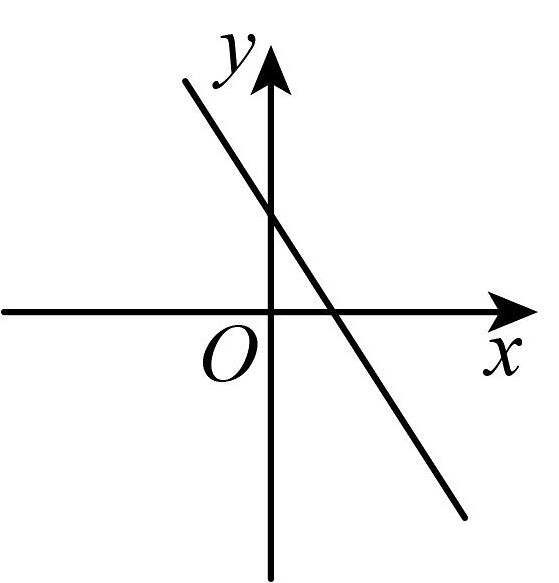 C、
C、 D、
D、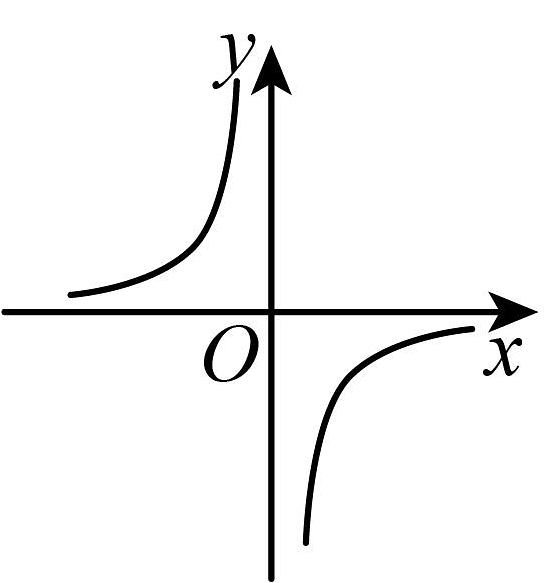
-
9、某班级共有位学生,现将个枇杷作为午餐水果分发给学生.若每人发2个,则还剩10个;若每人发3个,则还缺30个.下列四个方程:
①;②;③;④ , 其中符合题意的是( )
A、①③ B、②④ C、①④ D、②③ -
10、如图,在中, , , , 把绕直线旋转一周,所得几何体的侧面积为( )
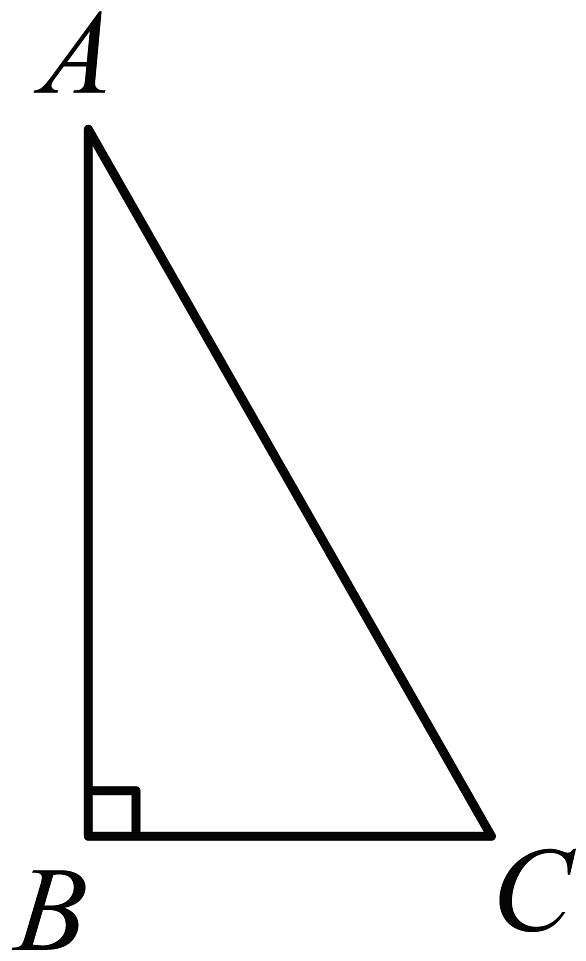 A、 B、 C、 D、
A、 B、 C、 D、 -
11、如图是一张横格数学作业纸,纸中的横线都平行,且相邻两条横线间的距离都相等.线段在横格纸上,与作业本的横线交于点 , 若 , 则的长是( )
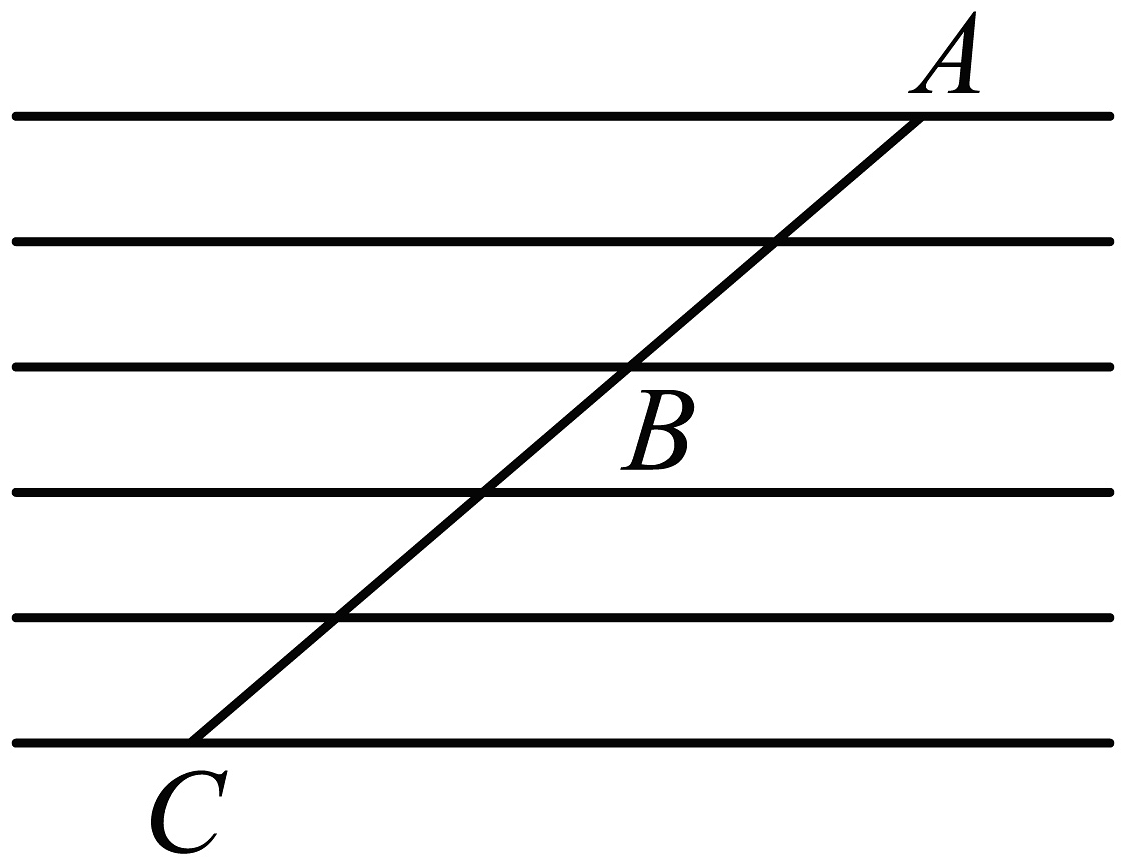 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8 -
12、下列计算正确的是( )A、 B、 C、 D、
-
13、如图,点 , , 在上, , 则的度数为( )
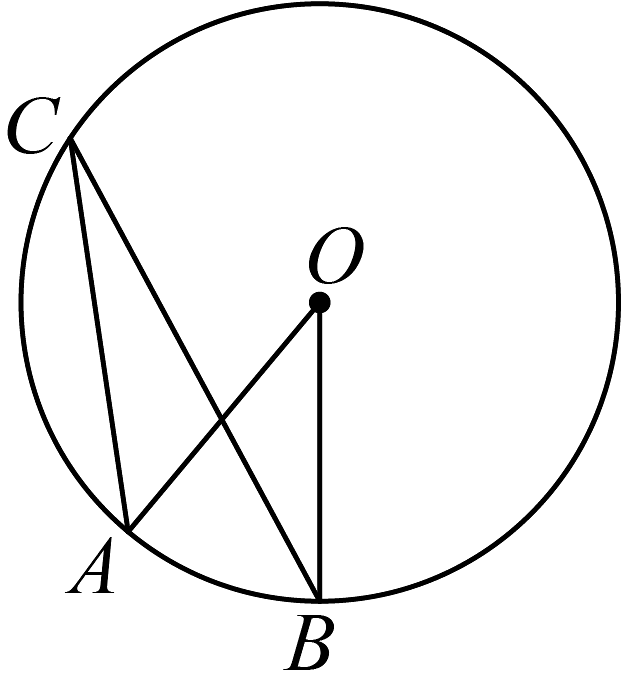 A、 B、 C、 D、
A、 B、 C、 D、 -
14、的相反数是( )A、 B、 C、 D、
-
15、下列各数中最小的是( )A、0 B、 C、 D、
-
16、新定义:若一个点的横坐标与纵坐标之和为6,那么称这个点为“和六点”.已知反比例函数的图象经过点 , 二次函数的图象经过该反比例函数图象上的所有“和六点”.(1)、求该二次函数的解析式;(2)、若 , 请直接写出的解集;(3)、已知二次函数与反比例函数的图象交于(点的横坐标小于点的横坐标)两点,为抛物线对称轴上一动点.若是以为顶点的等腰三角形,求点的坐标.
-
17、2024年第四届国际龙舟联合会世界杯在汨罗市汨罗江国际龙舟竞渡中心开赛,预计来自全国各地1000余名选手将参赛.汨罗江两岸高颜值的绿色生态景观绿化带“汨罗之窗”将迎接汨罗市民以及来自全国各地的朋友近距离的观看比赛.比赛设置男子组、女子组、本地组三个组别,其中男子组将进行:100米直道竞速赛,:200米直道竞速赛,:500米直道竞速赛,:3000米绕标赛.为了了解汨罗市民对于这四个比赛项目的关注程度,随机对部分市民进行了问卷调查(参与问卷调查的每位市民只能选择其中一个项目),将调查得到的数据绘制成数据统计表和扇形统计图(表、图都未完全制作完成):
市民最关注的比赛项目人数统计表
比赛项目
关注人数
42
30
 (1)、直接写出、的值和所在扇形圆心角的度数;(2)、若当天观看比赛的市民有10000人,试估计当天观看3000米绕标赛的市民有多少人?(3)、为了缓解比赛当天城市交通压力,维护交通秩序,汨罗交警支队派出4名交警(2男2女)对该路段进行值守,若在4名交警中任意抽取2名交警安排在同一路口执勤,请用列举法(画树状图或列表)求出恰好抽到的两名交警性别相同的概率.
(1)、直接写出、的值和所在扇形圆心角的度数;(2)、若当天观看比赛的市民有10000人,试估计当天观看3000米绕标赛的市民有多少人?(3)、为了缓解比赛当天城市交通压力,维护交通秩序,汨罗交警支队派出4名交警(2男2女)对该路段进行值守,若在4名交警中任意抽取2名交警安排在同一路口执勤,请用列举法(画树状图或列表)求出恰好抽到的两名交警性别相同的概率. -
18、如图,是等边三角形,点D在上,点E在的延长线上,且 .
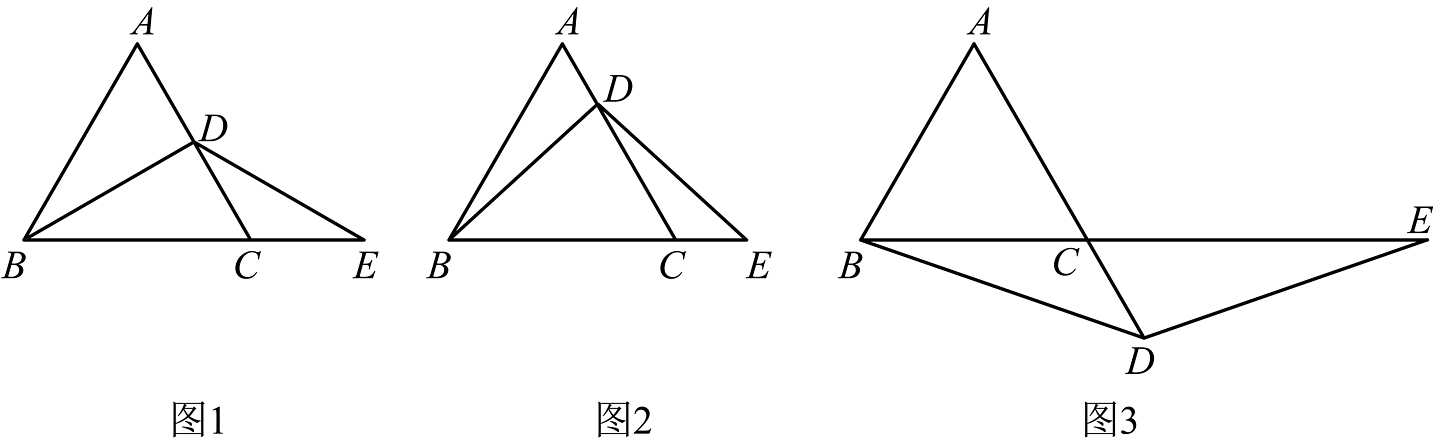 (1)、如图(1),若点D是的中点,求证:;(2)、如图(2),若点不的中点,是否成立?证明你的结论;(3)、如图(3),若点在线段的延长线上,试判断与的大小关系,并说明理由.
(1)、如图(1),若点D是的中点,求证:;(2)、如图(2),若点不的中点,是否成立?证明你的结论;(3)、如图(3),若点在线段的延长线上,试判断与的大小关系,并说明理由. -
19、如图,直线l与相切于点D,为的直径,过点A作于点E,延长交直线l于点C.
 (1)、求证:平分;(2)、如果 , , 求的半径.
(1)、求证:平分;(2)、如果 , , 求的半径. -
20、先化简,再求值: , 其中 .