-
1、某校在推进新课程改革的过程中,自主开发了五门校本课程,分别是: . 人工智能探索; . 传统文化寻根; . 体质与健康; . 山歌唱四方; . 书香润心.每名同学根据自己的爱好只能选择其中一门课程,学校对全校同学的选课情况进行了随机抽样调查,制成了如图所示的两幅不完整的统计图.
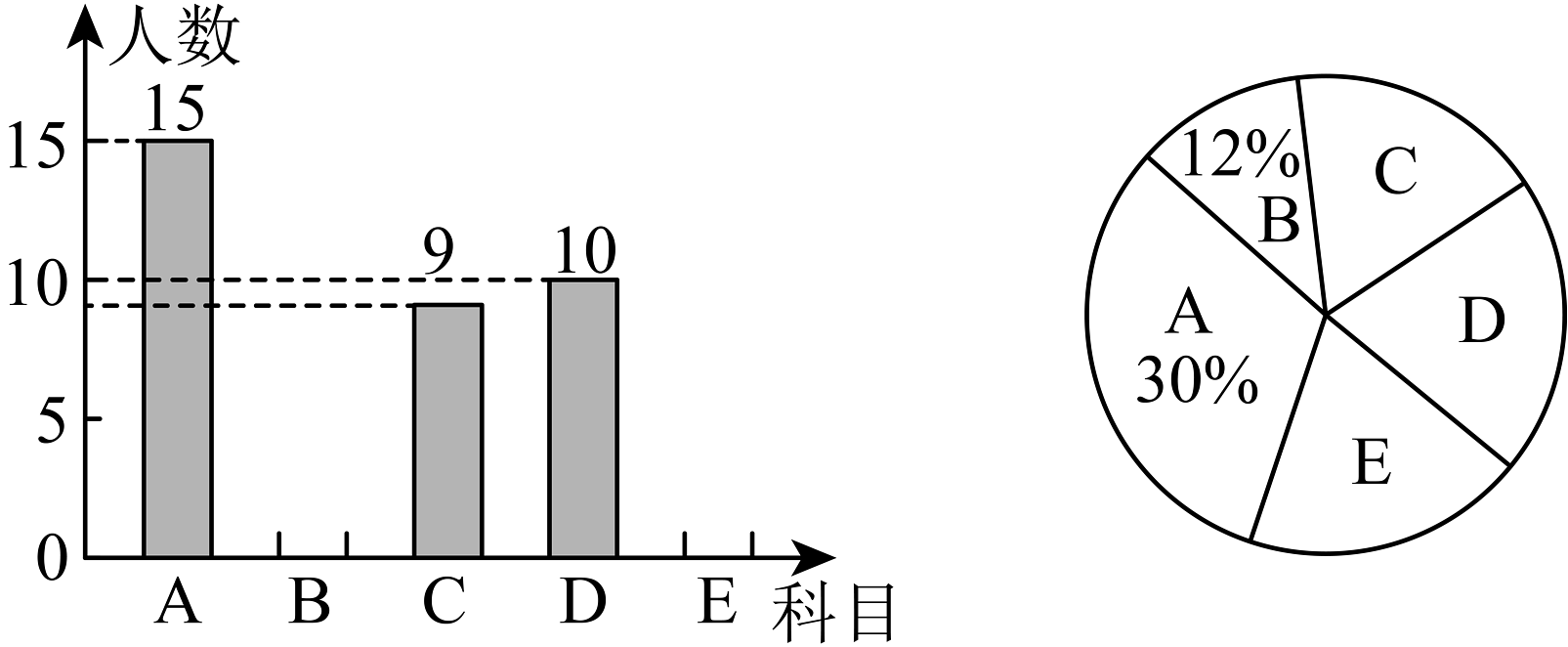 (1)、补全条形统计图,课程所在的扇形的圆心角的度数是____;(2)、若该校有名学生,请你估计该校选择课程的学生有多少名?(3)、某班有名同学,其中名同学选择课程 , 名同学选择课程 , 名同学选择课程 . 若从这名同学中随机抽取名同学,请你用列表法或画树状图的方法求抽取的这名同学都是选择课程的概率.
(1)、补全条形统计图,课程所在的扇形的圆心角的度数是____;(2)、若该校有名学生,请你估计该校选择课程的学生有多少名?(3)、某班有名同学,其中名同学选择课程 , 名同学选择课程 , 名同学选择课程 . 若从这名同学中随机抽取名同学,请你用列表法或画树状图的方法求抽取的这名同学都是选择课程的概率. -
2、如图,四边形是平行四边形,是边上的一点,且 .
 (1)、尺规作图:作的平分线 , 交于点(不写作法,保留作图痕迹).(2)、连接 . 求证:四边形是菱形.
(1)、尺规作图:作的平分线 , 交于点(不写作法,保留作图痕迹).(2)、连接 . 求证:四边形是菱形. -
3、(1)计算;
(2)解方程组: .
-
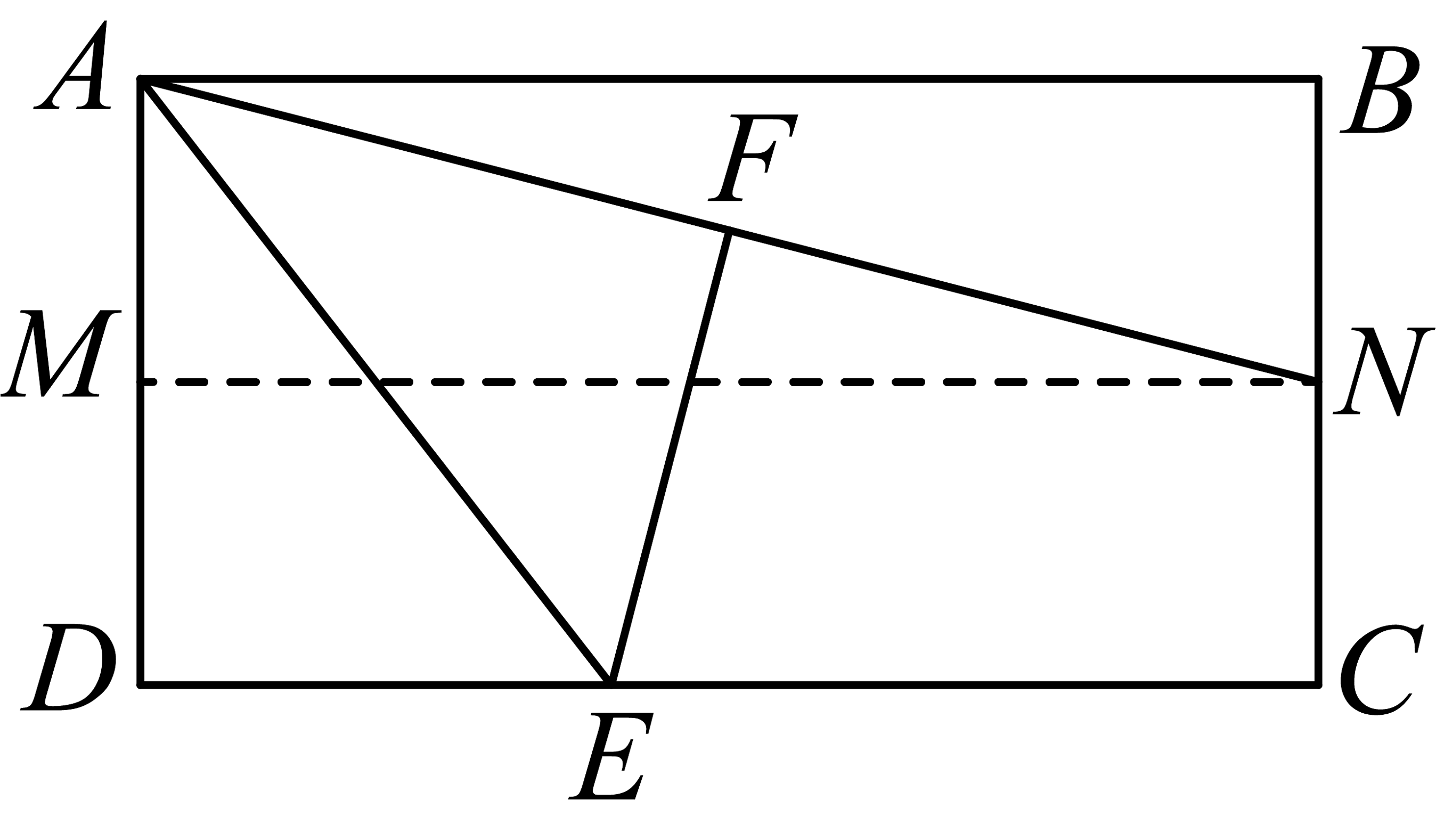
4、如图,将矩形纸片对折,使与重合,得到折痕;将纸片展平,连接 , 把沿翻折得到 , 点恰好落在的中点处.若 , 则的长为 .
-
5、“海棠花窗”是中国建筑中常见的一种设计.如图是一个海棠花窗的制作示意图,点是正方形的边心距上的一点,以点为圆心,长为半径画弧 , 同样的作法得到其余三条和弧一样的等弧,已知正方形的边长是6,当时,这个海棠花窗的周长是 .

-
6、如图,一次函数的图象与反比例函数()的图象相交于点 , 与轴相交于点 , 把线段绕点逆时针旋转 , 若点的对应点在函数的图象上,则的值为( )
 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9 -
7、如图,四边形内接于 , 为直径, , 连接 . 若半径为3, . 则的长为( )
 A、 B、 C、 D、2
A、 B、 C、 D、2 -
8、已知点 , , 在同一个函数的图象上,其中 , 这个函数可能是( )A、 B、 C、 D、
-
9、根据《铁路互联网售票管理办法》,对于持二代居民身份证购买“、”字头列车车票的旅客,可以不用取票直接刷身份证进站,这样能够缩短旅客排队购票、取票的等待时间.已知采用刷身份证进站的方式后平均每分钟进站的旅客人数是原来的3倍,且300名旅客的进站的时间比原来200名旅客的进站时间还少5分钟,设原来平均每分钟进站旅客的人数是人.列出方程为( )A、 B、 C、 D、
-
10、下列计算正确的是( )A、 B、 C、 D、
-
11、如图,在中, , , 是的垂直平分线,分别交、于点 , , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、已知点是正比例函数图象上一点,则下列点也在该函数图象上的是( )A、 B、 C、 D、
-
13、如图,在中,点 , 分别是 , 的中点, , 则的长为( )
 A、6 B、4 C、3 D、2
A、6 B、4 C、3 D、2 -
14、平陆运河改变了广西临海但没有江河直接通航入海的现状.截至年6月,平陆运河项目累计完成投资约为元,将数据用科学记数法表示为( )A、 B、 C、 D、
-
15、如图所示的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
16、的绝对值是( )A、 B、 C、 D、
-
17、如图,抛物线与轴交于、两点,与轴交于点是线段上的一个动点(不与端点重合),过点作轴的垂线,交抛物线于点 , 交直线于点 .
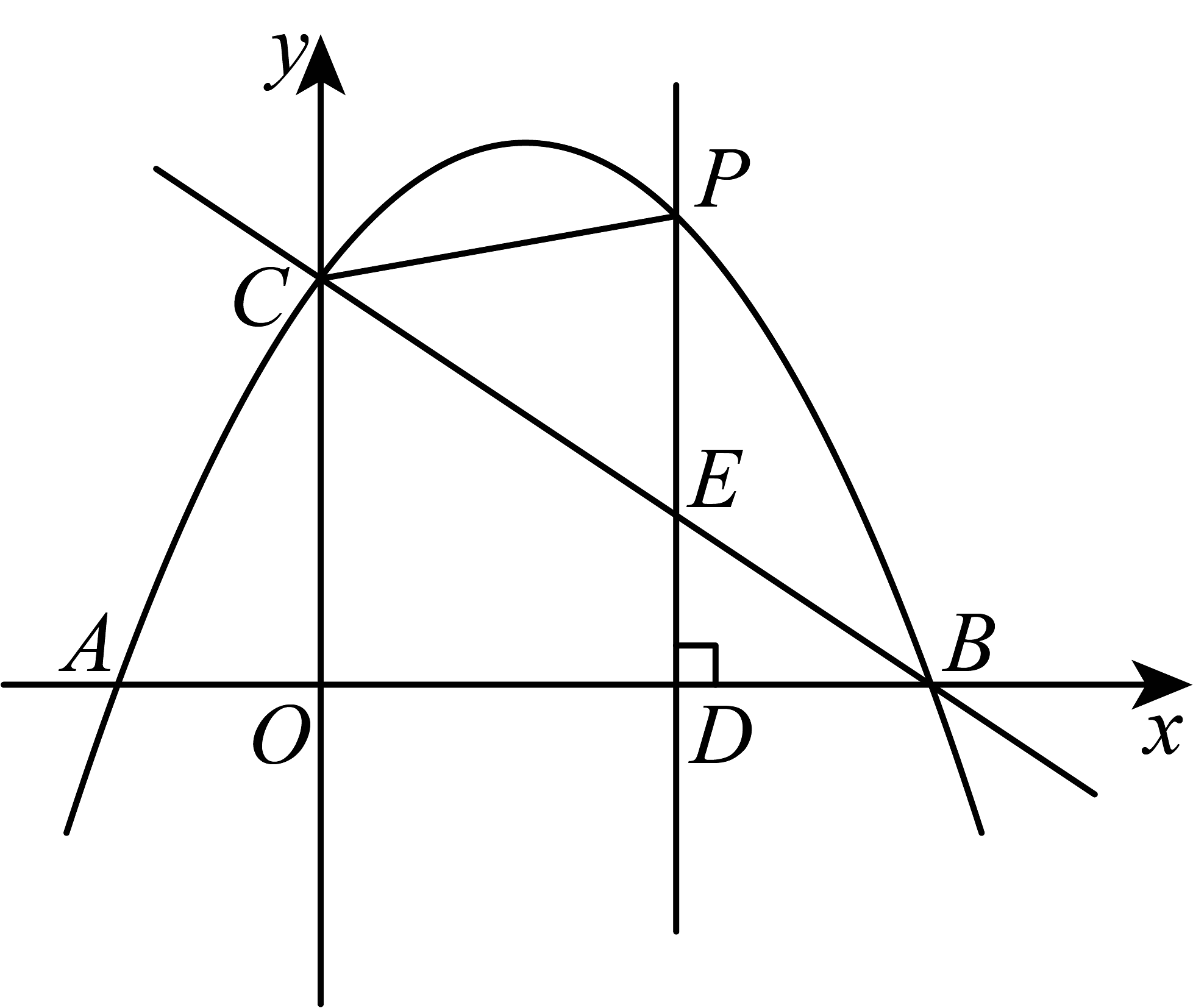 (1)、求抛物线的解析式;(2)、当时,求的长;(3)、若以、、为顶点的三角形与相似,求点的坐标.
(1)、求抛物线的解析式;(2)、当时,求的长;(3)、若以、、为顶点的三角形与相似,求点的坐标. -
18、如图,是的内接三角形,是的直径,点是上的点,且 , 连接 , 过点作的切线,交的延长线于点 , 交的延长线于点 .
 (1)、求证:;(2)、过点作于点 , 交于点 , 若 , , 求的长.
(1)、求证:;(2)、过点作于点 , 交于点 , 若 , , 求的长. -
19、如图,一次函数的图象与轴,轴分别交于点A,B,与反比例函数的图象交于点和点 , 其中点的纵坐标是2.
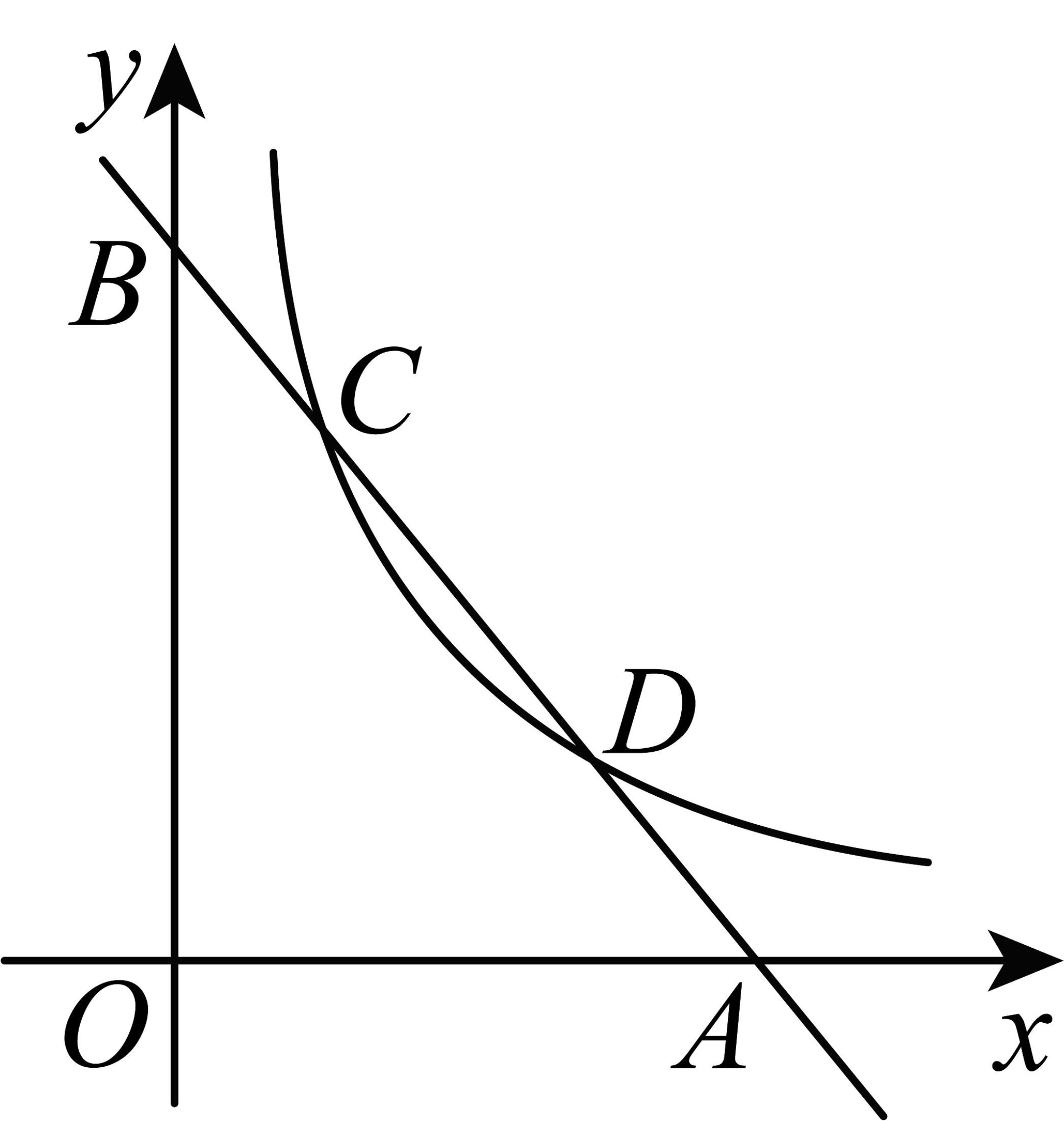 (1)、求反比例函数的解析式和点的坐标;(2)、点是反比例函数上的一点,轴交直线于点 , 若以、P、Q、O为顶点的四边形为平行四边形,求出点的坐标.
(1)、求反比例函数的解析式和点的坐标;(2)、点是反比例函数上的一点,轴交直线于点 , 若以、P、Q、O为顶点的四边形为平行四边形,求出点的坐标. -
20、如图,某渔船在处测得小岛位于的北偏西方向,小岛位于的北偏东方向.该渔船沿正北方向航行一段时间后到达处,此时测得小岛位于的南偏西方向.且相距15海里,小岛位于的南偏东方向.
 (1)、求该渔船航行的距离;(2)、求处与小岛之间的距离(结果取整数).参考数据: , , .
(1)、求该渔船航行的距离;(2)、求处与小岛之间的距离(结果取整数).参考数据: , , .