-
1、如图,在矩形中, , , 反比例函数的图象与矩形两边 , 分别交于点E,F.
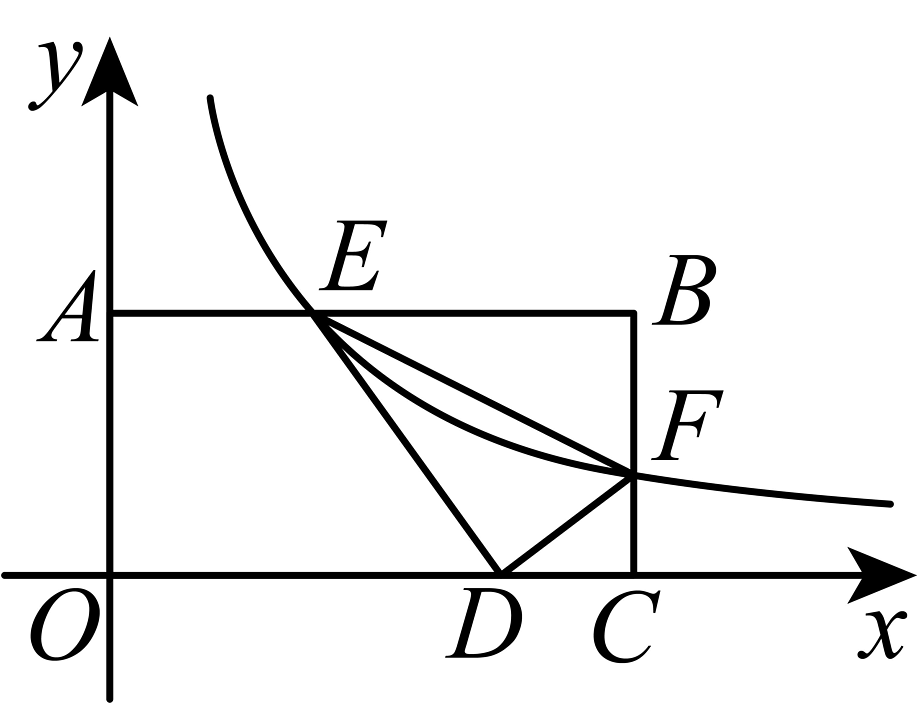 (1)、若E是的中点,求反比例函数的解析式;(2)、若 , 将沿直线对折,点B落在x轴上的点D处,求点D的坐标.
(1)、若E是的中点,求反比例函数的解析式;(2)、若 , 将沿直线对折,点B落在x轴上的点D处,求点D的坐标. -
2、(1)计算∶
(2)先化简,再求值 , 其中
-
3、如图,矩形的顶点C在反比例函数的图象.上,反比例函数的图象与 , 分别交于点E,F,轴于点H,轴于点G,与相交于点M.有下列说法:①矩形的面积是1;②的面积是 ;③矩形与矩形的面积一定相等;④若的面积为 , 矩形的面积为 , 则必有 . 其中说法正确的是(填序号).

-
4、在一个口袋中有个完全相同的小球,把它们分别标号为、、、 , 随机摸取一个小球然后放回,再随机摸取一个小球,两次摸出小球的标号和等于的概率是 .
-
5、如图,已知 , 则
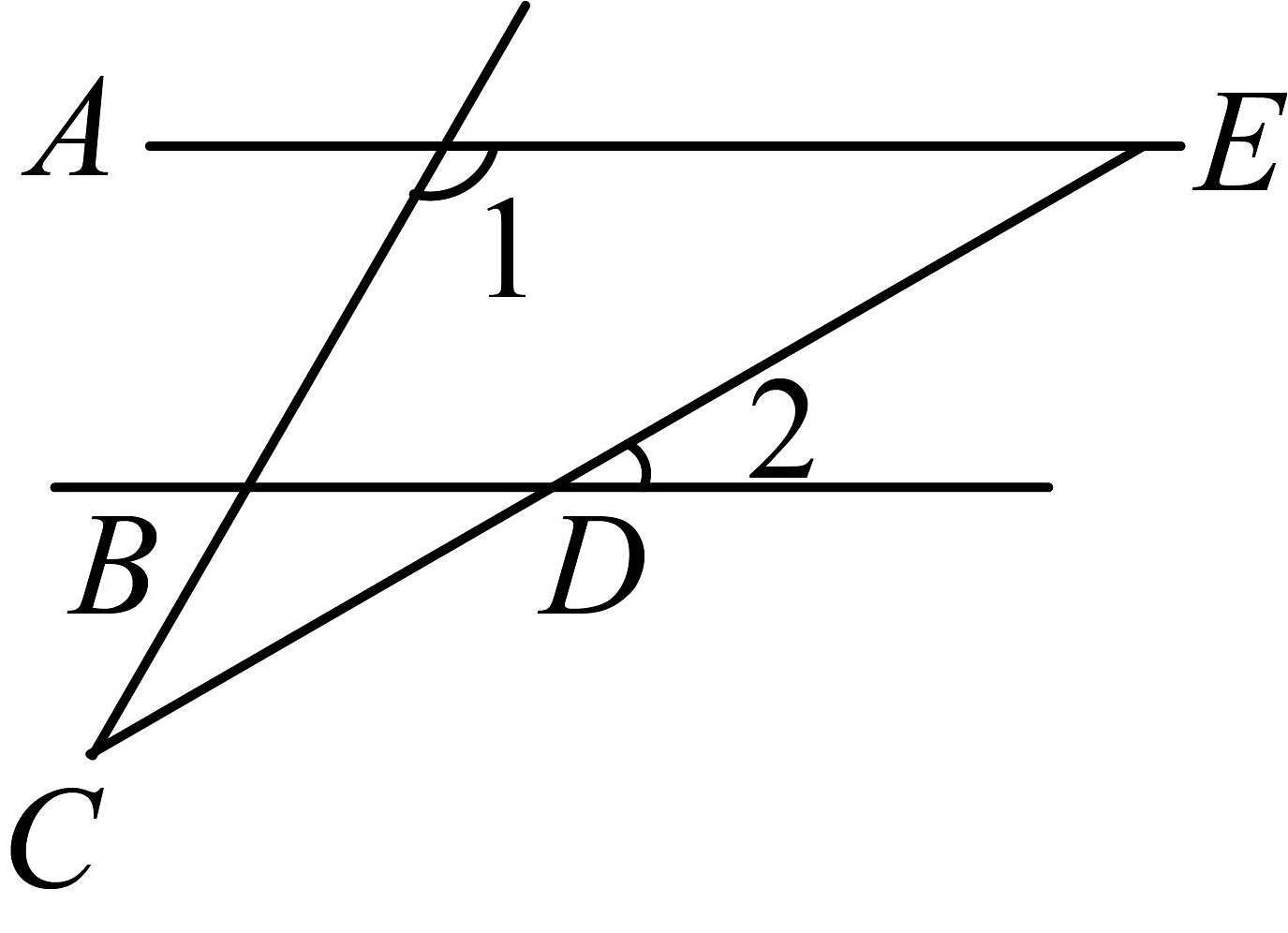
-
6、如图,矩形中, , , 为边上点,以为圆心,为半径作的一部分 , 其中点在边上,且与相切,延长至平分 , 平分 , 则长度是( )
 A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米 -
7、如图,从A处观测铁塔顶部的仰角是 ,向前走50米到达B处,观测铁塔的顶部的仰角是 , 则铁塔的高度是( )
 A、米 B、米 C、米 D、米
A、米 B、米 C、米 D、米 -
8、已知二次函数(a ,b,c为常数)的图象如图所示,则一次函数与反比例函数 在同一平面直角坐标系内的大致图象是( )
 A、
A、 B、
B、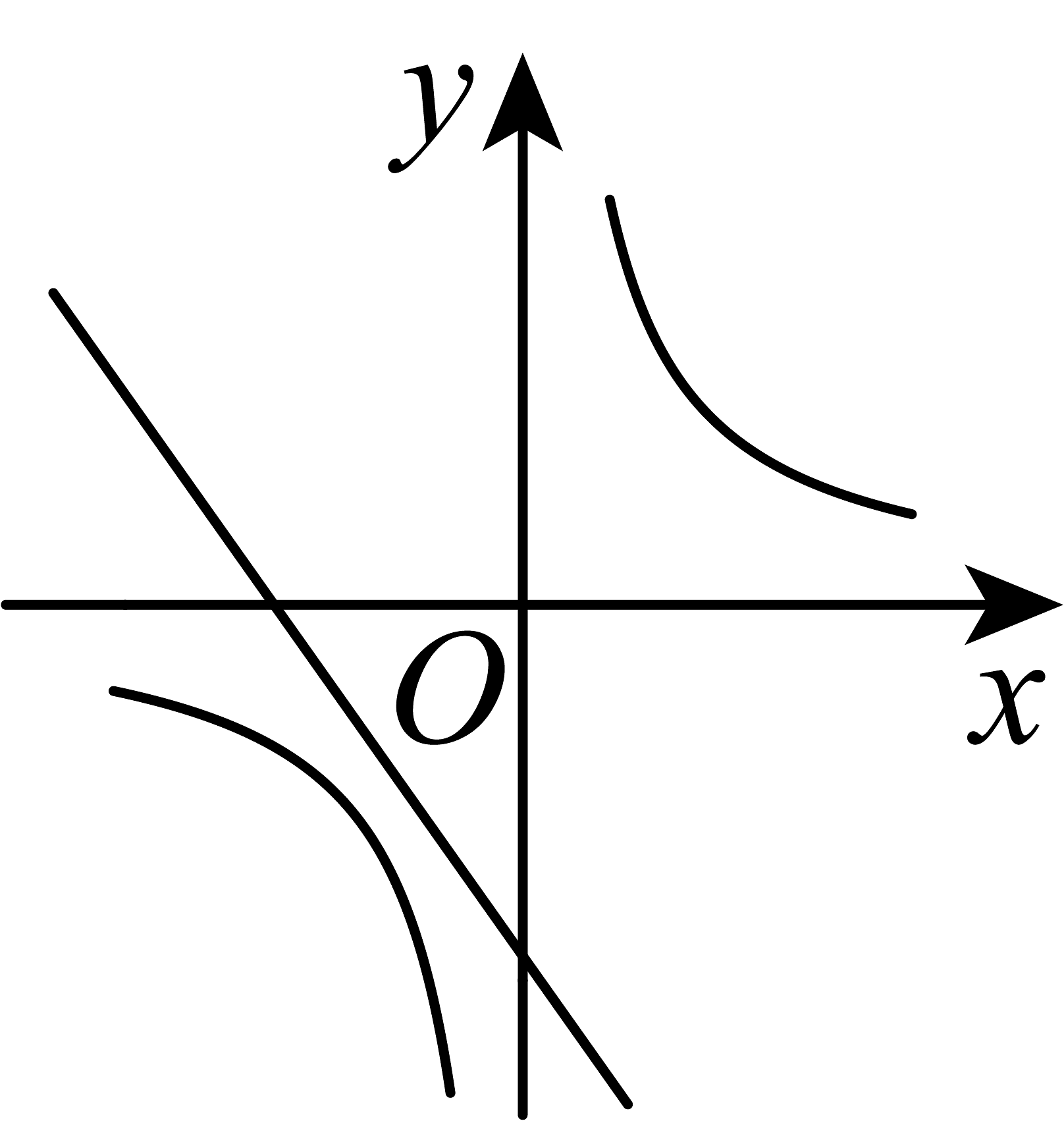 C、
C、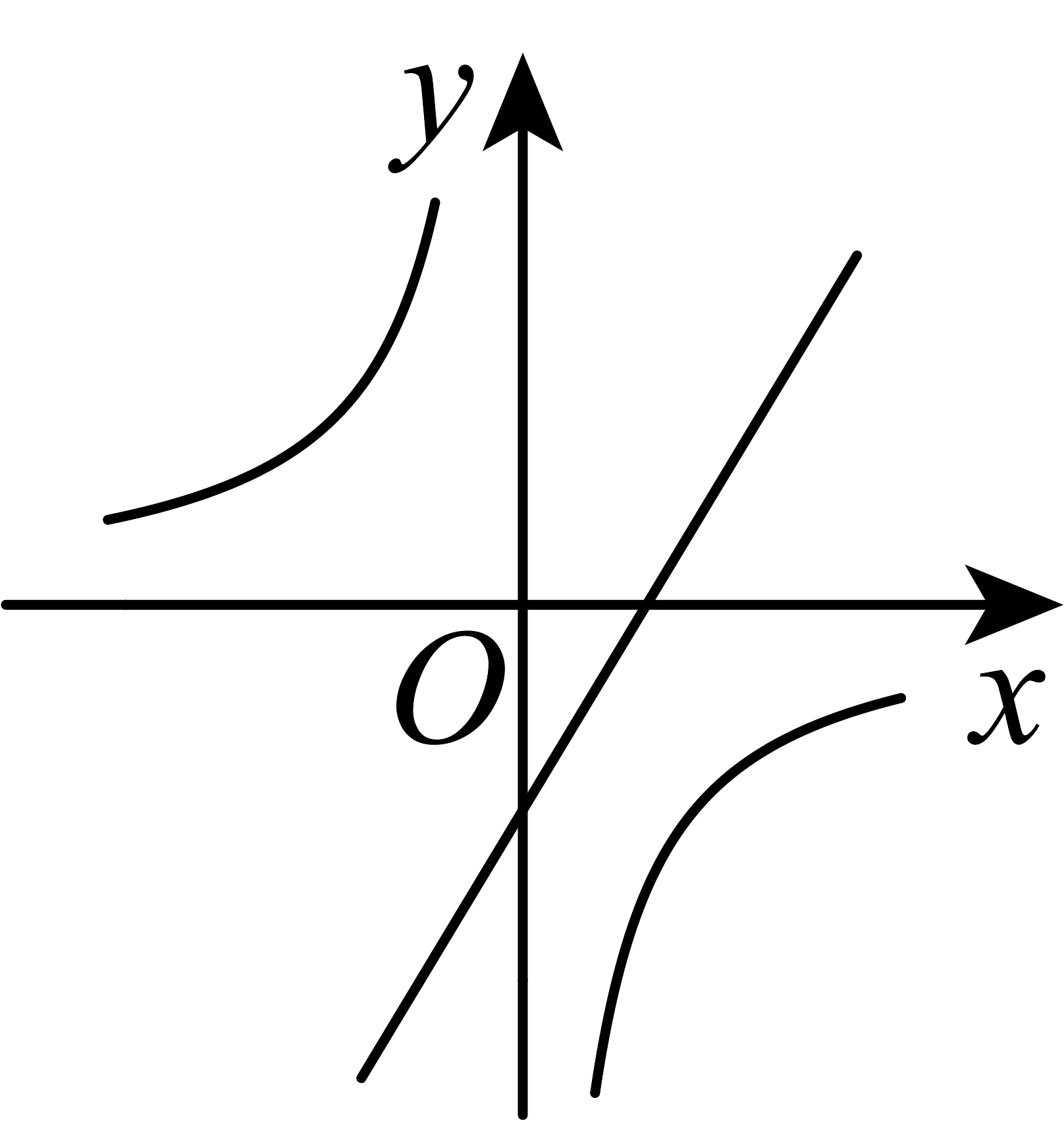 D、
D、
-
9、下列计算正确的是( )A、 B、 C、 D、
-
10、如图,的直径垂直于弦 , 垂足为E, , , 则的长为( )
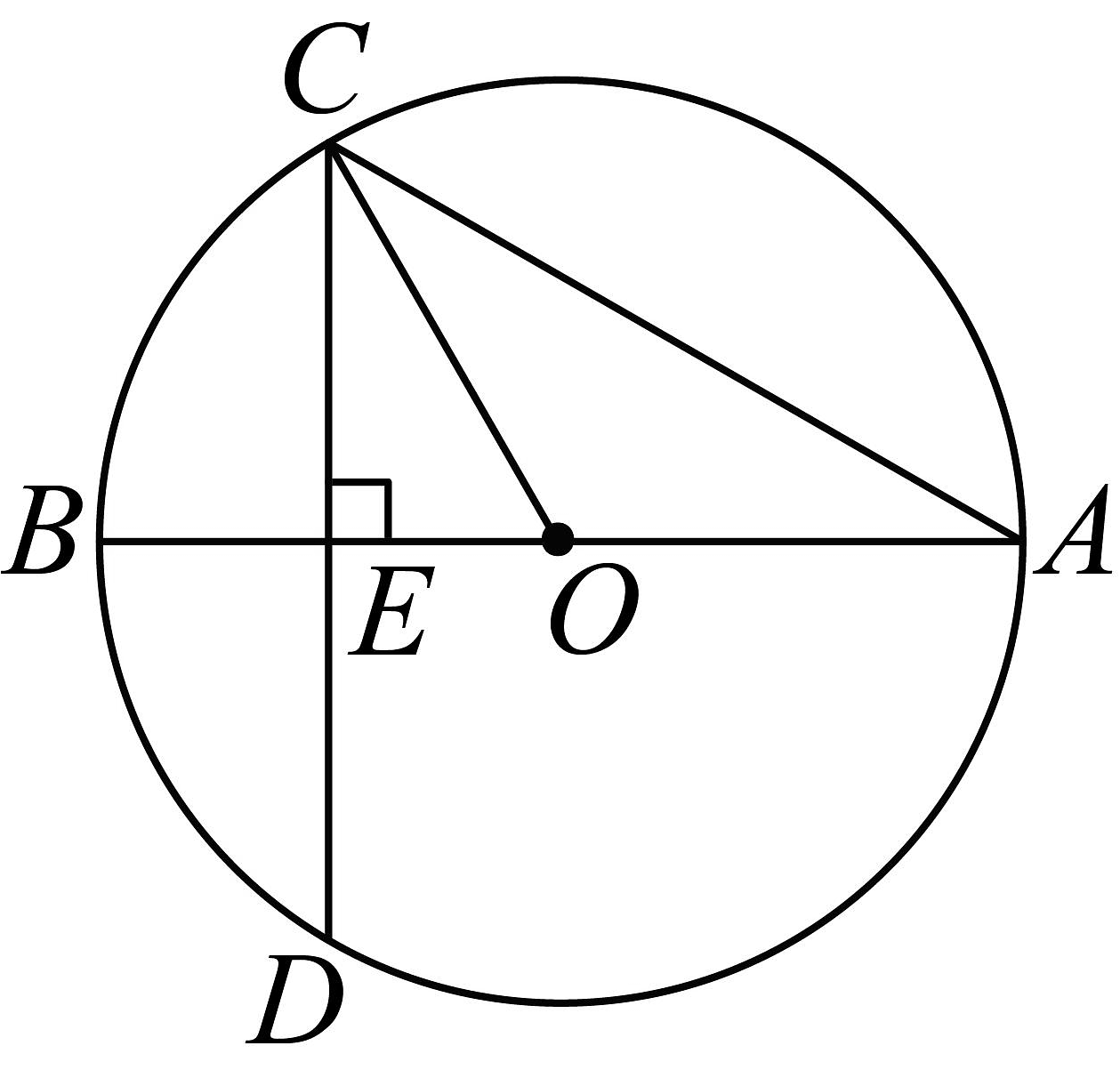 A、 B、 C、 D、6
A、 B、 C、 D、6 -
11、如果将抛物线向右平移1个单位长度,再向下平移2个单位长度,那么所得的抛物线的解析式是( )A、 B、 C、 D、
-
12、一组数据3,4,6,8,x,7的众数是7,则另一组数据4,3,6,8,2,x的中位数是( )A、3 B、4 C、5 D、6
-
13、下面的图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、
-
14、据交通部门统计,某地区春节期间客运量达到170 000 000人次,将170 000 000用科学记数法表示应是( )A、 B、 C、 D、
-
15、如图1,为的外接圆,且 , 点为圆外一动点,且满足 , 连结 , 交于点 , 交于点 , 连结 .
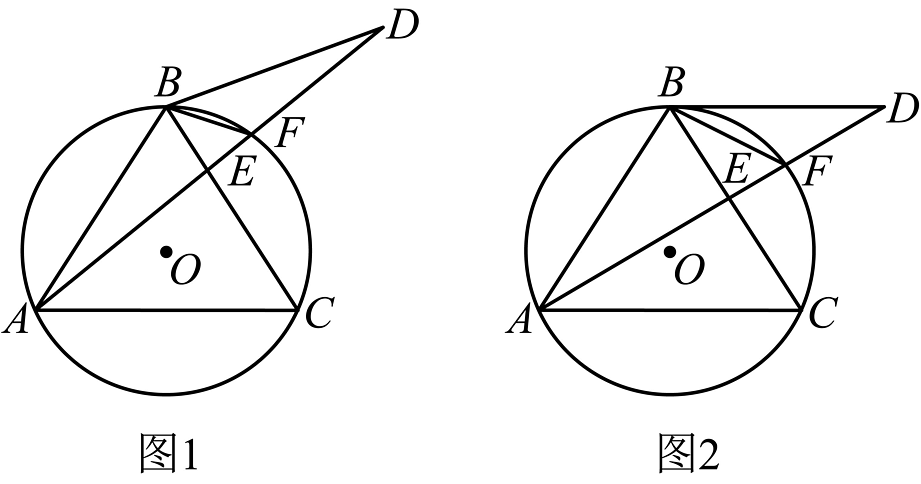 (1)、若经过圆心 , 求的长;(2)、求证:平分;(3)、如图2,若 , 设 , 请用含的代数式表示 .
(1)、若经过圆心 , 求的长;(2)、求证:平分;(3)、如图2,若 , 设 , 请用含的代数式表示 . -
16、设二次函数 .(1)、若该函数的对称轴为直线 . 求该函数的顶点坐标;(2)、判断该函数是否存在最大值5,若存在,求出的值;若不存在,请说明理由;(3)、已知点 , 和在函数图象上,当时,都有 , 求的取值范围.
-
17、定义:将一组对角线相同,另一组对角线共线的菱形称为“组合菱形”,内部菱形与外部菱形的共线对角线长之比称为组合比,用表示.如图,菱形和菱形是组合菱形,其中与共线,且满足 .
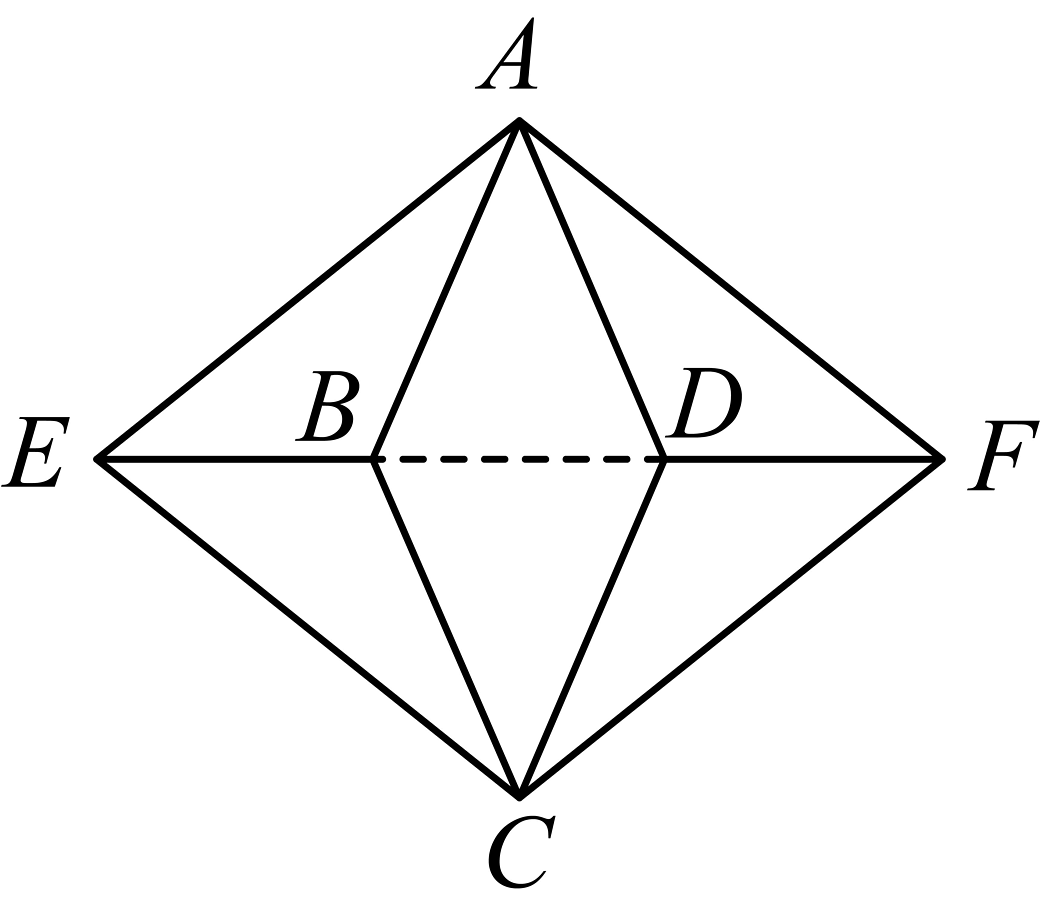 (1)、组合比___________;(2)、若 , 求的长;(3)、若 , 求证: .
(1)、组合比___________;(2)、若 , 求的长;(3)、若 , 求证: . -
18、某项目学习小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,当人和木板对湿地的压力(单位:)一定时,木板面积(单位:)与人和木板对地面的压强(单位:)成反比例.当木板面积为时,人和木板对地面的压强为 .(1)、求关于的函数表达式;(2)、当木板面积为时,压强是多少?(3)、如果要求压强不超过 , 木板面积至少要多大?请说明理由.
-
19、中国的人工智能领域近年来取得了显著的进展,并推动了技术在各行各业的普及和应用.小城同学采用抽样调查的方式对九年级部分同学做了“我最常使用的软件”的问卷调查,并根据调查收集的数据,绘制了如下的统计图表:
九年级学生最常使用的“”软件统计表
软件
使用人数
百分比
18
12
豆包
腾讯元宝
6
其他软件
8%
九年级学生最常使用的“软件统计图”
 (1)、请写出统计表中的值:
(1)、请写出统计表中的值:___________,___________;
(2)、已知九年级有400位同学,试估算最常使用“”的同学有多少位?(3)、小城了解到:使用“”和“”组合生成的效果很好,堪称“王炸组合”.现从“”、“”、“豆包”和”腾讯元宝”这四款软件中挑出两款,求挑出的恰好是""和""的概率. -
20、在中,平分 , 是边上的高, .
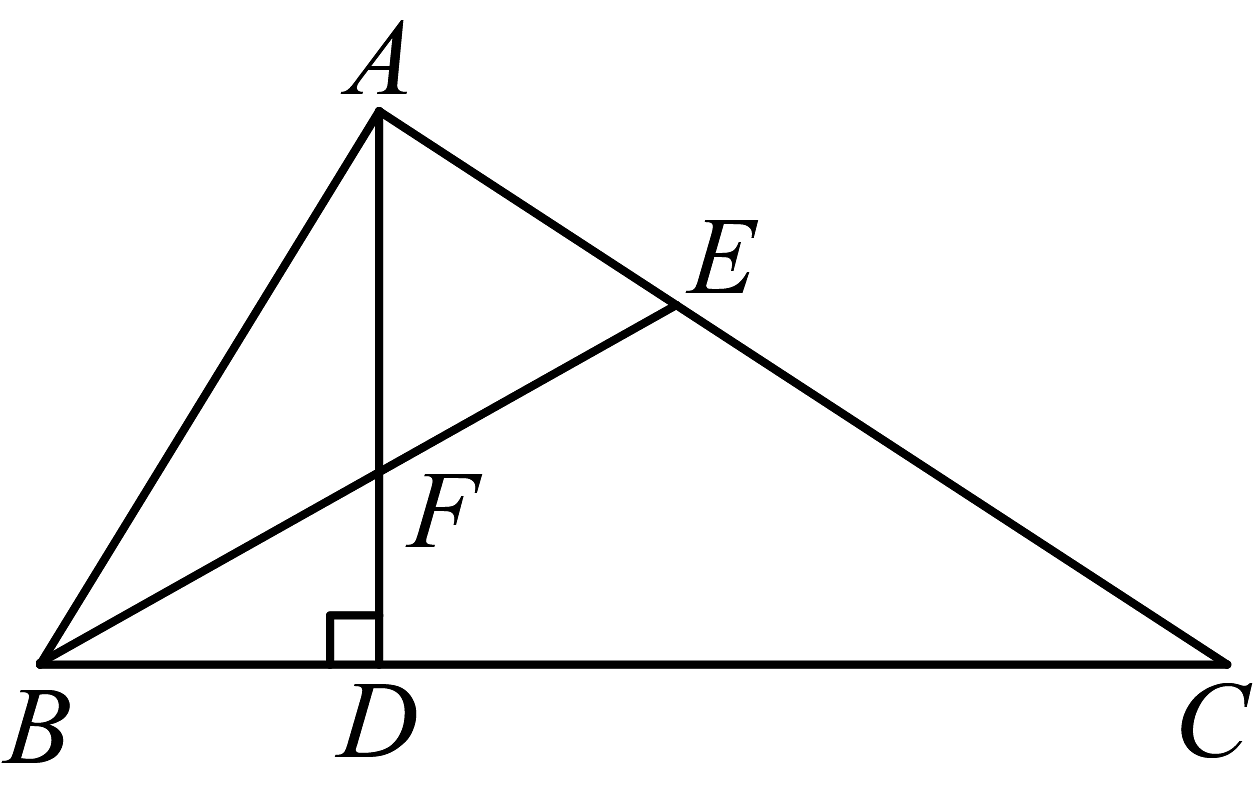 (1)、求的度数;(2)、若 , 求的长度.
(1)、求的度数;(2)、若 , 求的长度.