相关试卷

1、下列各数中最小的是（）

A、0 B、 $- 1$ C、 $- 2$ D、 $- 3$

查看解析
2、新定义：若一个点的横坐标与纵坐标之和为6，那么称这个点为“和六点”．已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A (2, 4)$ ，二次函数 $y = a x^{2} + b x (a \neq 0)$ 的图象经过该反比例函数图象上的所有“和六点”．

(1)、求该二次函数的解析式；

(2)、若 $x > 0$ ，请直接写出 $\frac{k}{x} > a x^{2} + b x$ 的解集；

(3)、已知二次函数与反比例函数的图象交于 $A, B$ （点 $A$ 的横坐标小于点 $B$ 的横坐标）两点， $P$ 为抛物线对称轴上一动点．若 $△ P A B$ 是以 $A$ 为顶点的等腰三角形，求点 $P$ 的坐标．

查看解析
3、2024年第四届国际龙舟联合会世界杯在汨罗市汨罗江国际龙舟竞渡中心开赛，预计来自全国各地1000余名选手将参赛．汨罗江两岸高颜值的绿色生态景观绿化带“汨罗之窗”将迎接汨罗市民以及来自全国各地的朋友近距离的观看比赛．比赛设置男子组、女子组、本地组三个组别，其中男子组将进行 $A$ ：100米直道竞速赛， $B$ ：200米直道竞速赛， $C$ ：500米直道竞速赛， $D$ ：3000米绕标赛．为了了解汨罗市民对于这四个比赛项目的关注程度，随机对部分市民进行了问卷调查（参与问卷调查的每位市民只能选择其中一个项目），将调查得到的数据绘制成数据统计表和扇形统计图（表、图都未完全制作完成）：
市民最关注的比赛项目人数统计表
比赛项目
$A$
$B$
$C$
$D$
关注人数
42
30
$a$
$b$

(1)、直接写出 $a$ 、 $b$ 的值和 $D$ 所在扇形圆心角的度数；

(2)、若当天观看比赛的市民有10000人，试估计当天观看3000米绕标赛的市民有多少人？

(3)、为了缓解比赛当天城市交通压力，维护交通秩序，汨罗交警支队派出4名交警（2男2女）对该路段进行值守，若在4名交警中任意抽取2名交警安排在同一路口执勤，请用列举法（画树状图或列表）求出恰好抽到的两名交警性别相同的概率．

查看解析
4、如图， $△ A B C$ 是等边三角形，点D在 $A C$ 上，点E在 $B C$ 的延长线上，且 $B D = D E$ ．

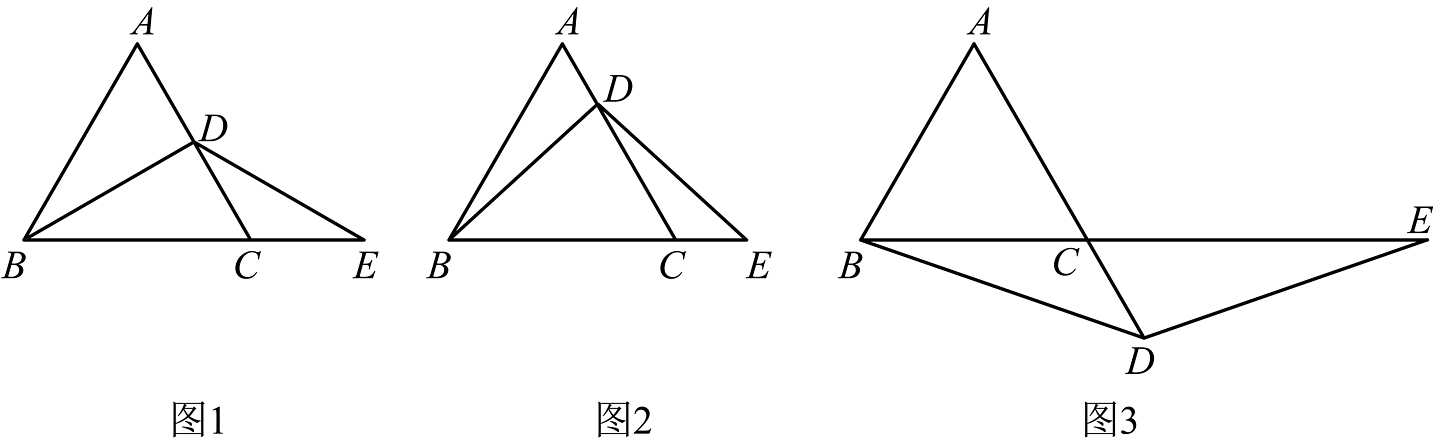(1)、如图（1），若点D是 $A C$ 的中点，求证： $A D = C E$ ；

(2)、如图（2），若点 $D$ 不 $A C$ 的中点， $A D = C E$ 是否成立？证明你的结论；

(3)、如图（3），若点 $D$ 在线段 $A C$ 的延长线上，试判断 $A D$ 与 $C E$ 的大小关系，并说明理由．

查看解析
5、如图，直线l与 $⊙ O$ 相切于点D， $A B$ 为 $⊙ O$ 的直径，过点A作 $A E ⊥ l$ 于点E，延长 $A B$ 交直线l于点C．

(1)、求证： $A D$ 平分 $∠ C A E$ ；

(2)、如果 $B C = 1$ ， $D C = 3$ ，求 $⊙ O$ 的半径．

查看解析
6、先化简，再求值： $(1 + \frac{2}{a - 1}) \div \frac{a^{2} - 1}{a^{2} - 2 a + 1} + a$ ，其中 $a = 2025$ ．

查看解析
7、计算： ${(\frac{1}{2})}^{- 1} + \sqrt{12} + |- 2026^{0}| - 4 sin 60 °$ ．

查看解析
8、已知抛物线 $y = - \frac{3}{16} (x - 1) (x - 9)$ 与x轴交于A，B两点，对称轴与抛物线交于点C，与x轴交于点D， $⊙ C$ 的半径为1，G为 $⊙ C$ 上一动点，P为 $A G$ 的中点，则 $D P$ 的最大值为．

查看解析
9、如图，是凸透镜成像规律中的一种情形， $A B ∥ E F$ ， $∠ B A O = 40 °$ ，则 $∠ F E C =$ °．

查看解析
10、若 $x = 2$ 是关于 $x$ 的一元二次方程 $a x^{2} - b x - 2 = 0$ 的解，则代数式 $2024 + 4 a - 2 b$ 的值是．

查看解析
11、在 $▱ A B C D$ 中， $∠ A B C$ 的角平分线交 $A D$ 于点 $E$ ，点 $E$ 分 $A D$ 为4和5两部分，则 $▱ A B C D$ 的周长为(　　)

A、24 B、26 C、28 D、26或28

查看解析
12、如图是某兰花爱好者随机抽取了5种蝴蝶兰，想从单枝上花朵的数量来描述其观赏性，每种兰花单枝上的花朵数标记在图中，问这组数据的中位数和众数是（）

A、4，4 B、4，9 C、5，9 D、9，9

查看解析
13、下列说法正确的是（）．

A、 $- 2$ 是 $- 4$ 的平方根 B、2是 ${(- 2)}^{2}$ 的算术平方根 C、 ${(- 2)}^{2}$ 的平方根是2 D、8的立方根是2或 $- 2$

查看解析
14、据悉，国家将在2035年前建成以北斗系统为核心的综合时空体系，以提供安全、便捷、高效的定位导航授时服务．截止目前，北斗产品应用总量已超过1550万台／套．数据15500000用科学记数法表示为（）

A、 $1.55 \times 10^{3}$ B、 $1.55 \times 10^{4}$ C、 $1.55 \times 10^{6}$ D、 $1.55 \times 10^{7}$

查看解析
15、蜜蜂的蜂巢美观有序，从入口处看，蜂巢由许多正六边形构成，则正六边形的对称轴有（）

A、2 B、3 C、6 D、12

查看解析
16、通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的 $.$ 下面是一个案例，请补充完整．

原题：如图 $1$ ，点 $E$ ， $F$ 分别在正方形 $A B C D$ 的边 $B C$ ， $C D$ 上， $∠ E A F = 45 °$ ，连接 $E F$ ，则 $E F = B E + D F$ ，试说明理由．

(1)、思路梳理
$∵ A B = C D$ ，
$∴$ 把 $△ A B E$ 绕点A逆时针旋转 $90 °$ 至 $△ A D G$ ，可使 $A B$ 与 $A D$ 重合.
$∵ ∠ A D C = ∠ B = 90 ° ， ∠ F D G = 180 °$ ， $∴$ 点 $F$ ， $D$ ， $G$ 共线 $.$ 根据______ $($ 从“ $SSS$ ， $A S A$ ， $A A S$ ， $S A S$ ”中选择填写 $)$ ，易证 $△ A F G ≌$ ______ ，得 $E F = B E + D F$ ．

(2)、类比引申
如图 $2$ ，四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 90 °$ ，点 $E$ ， $F$ 分别在边 $B C$ ， $C D$ 上， $∠ E A F = 45 ° .$ 若 $∠ B$ ， $∠ D$ 都不是直角，则当 $∠ B$ 与 $∠ D$ 满足等量关系______ 时，仍有 $E F = B E + D F$ ．

(3)、联想拓展
如图 $3$ ，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点 $D$ ， $E$ 均在边 $B C$ 上，且 $∠ D A E = 45 ° .$ 猜想 $B D$ ， $D E$ ， $E C$ 应满足的等量关系，并写出推理过程．

(4)、思维深化
如图 $4$ ，在 $△ A B C$ 中， $∠ B A C = 60 °$ ， $A B = A C$ ，点 $D$ ， $E$ 均在直线 $B C$ 上，点 $D$ 在点 $E$ 的左边，且 $∠ D A E = 30 °$ ，当 $A B = 4$ ， $B D = 1$ 时，直接写出 $C E$ 的长．

查看解析
17、问题初探
（1）综合与实践数学活动课上，张老师给出了一个问题：已知二次函数 $y = x^{2} + 2 x - 3$ ，当 $- 2 \leq x \leq 2$ 时， $y$ 的取值范围为___________；
①小伟同学经过分析后，将原二次函数配方成 $y = a {(x - h)}^{2} + k$ 的形式，确定抛物线对称轴为直线 $x = h$ ，通过 $- 2 、 h$ 和2的大小关系，分别确定了最大值和最小值，进而求出 $y$ 的取值范围；
②小军同学画出如图的函数图象，通过观察图象确定了 $y$ 的取值范围；请你很据上述两名同学的分析写出 $y$ 的取值范围是___________；
类比分析
（2）张老师发现两名同学分别从“数”和“形”的角度分析、解决何题，为了让同学们更好的感悟“数形结合”思想，张老师将前面问题变式为下面问题，请你解答；已知二次函数 $y = x^{2} + 2 x - 3$ 当 $a - 1 \leq x \leq a + 1$ 时，求 $y$ 的最大值．并写出 $a$ 的取值范围；
学以致用
（3）已知二次函数 $y = - x^{2} + 6 x - 5$ ，当 $a \leq x \leq a + 3$ 时，二次函数的最大值为 $y_{1}$ ，最小值为 $y_{2}$ ，若 $y_{1} - y_{2} = 3$ ．求 $a$ 的值．

查看解析
18、如图，在 $R t Δ A B C$ 中 $∠ C = 90 °$ ，点 $O$ ， $D$ 分别为 $A B$ ， $B C$ 的中点，连接 $O D$ ，作 $⊙ O$ 与 $A C$ 相切于点 $E$ ，在 $A C$ 边上取一点 $F$ ，使 $D F = D O$ ，连接 $D F$ ．

（1）判断直线 $D F$ 与 $⊙ O$ 的位置关系，并说明理由；
（2）当 $∠ A = 30 °$ ， $C F = \sqrt{2}$ 时，求 $⊙ O$ 的半径．

查看解析
19、在学校组织的跳绳比赛中，每班参加的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为10分，9分，8分，7分，现将801班和802班的成绩整理并绘制成如图的统计图．
请根据以上提供的信息解答下列问题：
（1）此次比赛中，801班成绩在C级以上（包括C级）的人数为　     　．
（2）将下列表格补充完整．

平均分（分）
中位数（分）
众数（分）
801班
8.76
9
　     　
802班
8.76
　     　
10
（3）根据信息分析，你认为两个班哪个班成绩好一些，请说明理由．

查看解析
20、如图，以正方形 $A B C D$ 顶点 $A$ 为圆心，对角线 $A C$ 为半径作弧交边 $A D$ 延长线于点 $E$ ，若 $A B = 4$ ，则图中阴影部分的面积为（结果保留π）．

查看解析

上一页 309 310 311 312 313 下一页跳转

	平均分（分）	中位数（分）	众数（分）
801班	8.76	9
802班	8.76		10

比赛项目	$A$	$B$	$C$	$D$
关注人数	42	30	$a$	$b$