相关试卷

1、若a＜b，则下列不等式一定成立的是（）

A、a+b＜2b B、a-c<b+c C、ac＜bc D、 $\frac{a}{c} ＜ \frac{b}{c}$

查看解析
2、甲、乙、丙、丁四名选手参加射击测试，每人射击10次，平均成绩均为9.5环，方差如下表所示：
选手
甲
乙
丙
丁
方差
9.5
9
10
0.95
则四名选手中成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看解析
3、下列运算结果正确的是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 $a^{6} \div a^{3} = a^{3}$ C、 $(a^{2})^{4} = a^{6}$ D、 $(2 a)^{3} = 6 a^{3}$

查看解析
4、二次根式 $\sqrt{x - 1}$ 中字母ェ的取值范围为（）

A、x>1 B、x≠l C、x≥1 D、x≤1

查看解析
5、某几何体的三视图如图所示，该几何体是（）

A、梭柱 B、圆柱 C、圆锥 D、球

查看解析
6、实数2的相反数为（）

A、-2 B、 $- \frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看解析
7、如图，已知AB是 $⊙ O$ 的直径，CD，CE都是 $⊙ O$ 的弦， $A B ⊥ C D$ 于点 $G$ ， CE交AG于点 $F$ ，且 $B D = D E$ ，连结BE，分别交AD，CD于点H，K.

(1)、求证： $B K = D K$ .

(2)、若 $D K = 5$ ， $D H = 6$ ，求 $⊙ O$ 的直径.

(3)、若点 $F$ 在半径OA上， $O F = \frac{1}{2} O G$ ，请直接写出 $\frac{E H}{H B}$ 的值.

查看解析
8、已知二次函数y=-（x+1）²+h（h为常数）的图象经过点A（-2，3）.

(1)、求此二次函数的表达式.

(2)、将抛物线先向左平移n（n>0）个单位，再向上平移5个单位，函数图象恰好经过原点，求n的值。

(3)、已知点（p，m），（q，m）在二次函数y=-（x+1）²+h的图象上，且-7<2p+3q<2，求m的取值范围.

查看解析
9、某景区的同一线路上依次有A，B，C三个景点（如图1）．小兴从A景点出发，步行3500米去C景点，共用时50分钟；同时，桐桐以每分钟60米的速度从B景点出发，步行1500米到达A景点，休息10分钟后，桐桐改成骑电动车去C景点，结果桐桐比小兴早5分钟到达C景点，两人行走时均为匀速运动，设小兴步行的时间为t（分），两人各自距A景点的路程s（米）与t（分）之间的函数图象如图2所示。

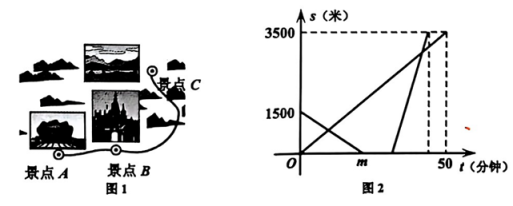(1)、求m的值，并说出m的实际意义

(2)、求桐桐骑车时距A景点的路程s（米）与t（分）之间的函数解析式（不必写出t的取值范围）；

(3)、请求出两人在途中相遇时的时间t（分）的值.

查看解析
10、尺规作图问题：
已知△ABC，∠ABC是钝角，AB>BC，请用尺规作AC的中点P.
小聪：如图1，以点A为圆心，BC长为半径作弧，以点C为圆心，AB长为半径作弧，两弧相交于点Q，连结BQ交AC于点P，则点P为AC的中点.
小明：如图2，作AB的中垂线，垂足为点M，作BC的中垂线，垂足为点N，以点M为圆心，BN为半径作弧，交AC边于点P，则点P为AC的中点.
小聪：小明，你的作法有问题，
小明：哦……我明白了.

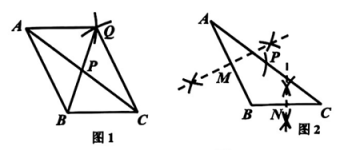(1)、证明：小聪的作法是正确的。

(2)、指出小明作法中存在的问题.

查看解析
11、睡眠状况对青少年的成长影响很大，为此，某校在随机选取的部分学生中开展了一次问卷调查活动，并制成以下尚不完整的统计图：
调査问卷
你每天的睡眠时长大约（）
A.少于8h
B.8～9h（不舍9h）
C.9~10h（不含10h）
D.不少于10h

(1)、求参加问卷调查的人数和m的值；

(2)、补全条形统计图；

(3)、若该校有1000名学生，估计该校每天睡眠时长少于8h的学生约为多少人？

查看解析
12、如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D， $A B = 10$ ， $s i n B = \frac{3}{5}$ .

(1)、求AD的长；

(2)、若 $B D = 2 C D$ ，求 $t a n C$ 的值.

查看解析
13、如图，点O是 $▱ A B C D$ 对角线AC的中点，沿过点O的直线MN将 $▱ A B C D$ 折叠，使点A，B分别落在A'，B'处，NB'交CD于点E，A'B'交AD于点F，若点E是CD的中点，且 $\frac{N E}{N C} = \frac{5}{3}$ ，则 $△ A M O$ 与四边形MOCD的面积比为.

查看解析
14、如图，在平面直角坐标系中，已知点A（2，4），B（3，2），以原点O为位似中心，作△OAB的位似图形△OA'B'，并把△OAB的边长缩小到原来的 $\frac{1}{2}$ ，则点A的对应点A'的坐标是.

查看解析
15、如图，BD是⊙O的直径，点A在DB的延长线上，AC是⊙O的切线，C为切点，连结CO，CD，若∠D=25°，则∠A的度数为.

查看解析
16、如图，将△ABC绕点B顺时针旋转90°得到△DBE，点A，C的对应点分别为点D，E，AC的延长线分别交BD，DE于点F，G，下列结论一定正确的是（）

A、BF=DF B、∠CBD=∠EBD C、CB∥DE D、AG⊥DE

查看解析
17、利用“配方法”解方程 $x^{2} - 4 x - 7 = 0$ ，配方结果正确的是（）

A、 $(x - 2)^{2} = 11$ B、 $(x - 2)^{2} = 3$ C、 $(x - 4)^{2} = 11$ D、 $(x - 4)^{2} = 3$ ：

查看解析
18、如图，平放在桌面上的烧杯中放着液体，当光线从空气射入液体中时，光线的传播方向会发生改变.若图中∠1=40°，∠2=30°，则∠3的度数为（）

A、30° B、40° C、60° D、70°

查看解析
19、综合与实践
我们已经学过，在△ABC中，若∠ABC=90°，则三角形三边满足勾股定理：AC²=AB²+BC².

(1)、【知识应用】
如图1，在△ABC中，AD⊥BC于点D，若AC>AB，则AC²-AB²=BC（CD-BD），请说明理由.

(2)、【拓展探究】
如图2，在△ABC中，AD⊥BC于点D，点E是AC的中点，连接BE.
求证：BE²- $\frac{1}{4}$ AC²=BD·BC.

(3)、【拓展应用】
如图3，在△ABC中，点E在边AB上（不与点A，B重合），点F在边BC上（不与点B，C重合），连接EF，∠BEF=∠BCA，点O为△BEF的外心，连接OA，OC，求证：OC²-OA²=BC²-BA².

查看解析
20、在直角坐标系中，设函数 $y = (x - m) (x - m - 2)$ （m是常数）.

(1)、当 $m = 5$ 时，求该函数图象与x轴的交点坐标.

(2)、若点A（n， $y_{1}$ $), B ($ $m + 1$ ， $y_{2}$ $), C ($ $x_{0}$ ， 3）都在该函数图象上，点A不与点B，C重合.
①比较 $y_{1}$ ， $y_{2}$ 的大小.
②若 $x_{0} = - 1$ ， $y_{1} > 3$ ，直接写出n的取值范围.

查看解析

上一页 311 312 313 314 315 下一页跳转

选手	甲	乙	丙	丁
方差	9.5	9	10	0.95