-
1、一元二次方程的一个解为 , 则 .
-
2、位于深圳市罗湖区的梧桐山公园自西南向东北渐次崛起,分布着小梧桐、豆腐头、大梧桐三大主峰.从远处观看,山中最为瞩目的当属小梧桐电视塔.登临小梧桐山顶,可上九天邀月揽星,可鸟瞰深圳关内外壮丽美景.我校某数学兴趣小组的同学准备利用所学的三角函数知识估测该塔的高度,已知电视塔位于坡度的斜坡上,测量员从斜坡底端处往前沿水平方向走了达到地面处,此时测得电视塔顶端的仰角为 , 电视塔底端的仰角为 , 已知、、、在同一平面内,则该塔的高度为( ) , (结果保留整数,参考数据; , )
 A、24 B、31 C、60 D、136
A、24 B、31 C、60 D、136 -
3、某村的居民自来水管道需要改造.该工程若由甲队单独施工恰好在规定时间内完成,若乙队单独施工,则完成工程所需天数是规定天数的1.8倍,如果由甲、乙两队先合作18天,那么余下的工程由甲队单独完成还需8天.设这项工程的规定时间是天,则根据题意,下面所列方程正确的是( )A、 B、 C、 D、
-
4、如图, , 则为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、在中,最小的实数是( )A、 B、0 C、 D、-3
-
6、如图,AC为的直径,四边形ABCD内接于 , , 连结BD交AC于点.
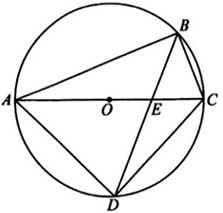 (1)、设 , 用含的代数式表示的度数;(2)、若 , 求的值;(3)、若 , 求面积的最大值.
(1)、设 , 用含的代数式表示的度数;(2)、若 , 求的值;(3)、若 , 求面积的最大值. -
7、如图1是钱塘老师和甬真老师相约去农庄参观的路线示意图.某日,钱塘老师从学校骑电动车匀速去往农庄,出发4min后,甬真老师从家里驾驶汽车匀速开往超市,在超市购物后,仍按原速行驶,最后两人同时到达农庄.用(单位:min)表示钱塘老师从学校出发后行驶的时间,用s(单位:km)表示两位老师距学校的路程.图2中,
线段OA是钱塘老师距学校的路程s关于:的函数图象.
 (1)、求线段OA表示的函数解析式.(2)、甬真老师从家出发至到达农庄的过程中,驾驶汽车的时长与在超市购物的时长相等。
(1)、求线段OA表示的函数解析式.(2)、甬真老师从家出发至到达农庄的过程中,驾驶汽车的时长与在超市购物的时长相等。①在图2中画出甬真老师距学校的路程s关于t(4≤t≤20)的函数图象;
②当t为何值时,两车行驶的路程相等。
-
8、已知二次函数 (a是常数).(1)、当时
①求二次函数图象的顶点坐标;
②在的范围内,求y的取值范围.
(2)、当a取值为 , ()时,二次函数的最大值相等,此时是否为定值?若是,求出该定值;若不是,请说明理由. -
9、如图,在△ABC中,AC=AB,∠BAC=90°,在AC右侧作等边三角形ACD.
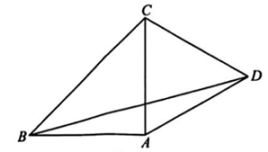 (1)、求∠CBD的度数;(2)、若BC=4,求BD的长度.
(1)、求∠CBD的度数;(2)、若BC=4,求BD的长度. -
10、为了解某校九年级学生“一分钟跳绳”成绩,学校随机抽取了若干名九年级学生进行跳绳测试,并将收集的跳绳成绩同时交给甲、乙两兴趣小组进行独立处理,图1、图2分别是甲、乙两兴趣小组绘制的跳绳成绩频数分布直方图(每个分组包含左端点,不含右端点).

根据以上信息,回答下列问题,
(1)、补全乙组绘制的跳绳成绩频数分布直方图;(2)、已知该校九年级共有700名学生,请估计“一分钟跳绳”成绩为180个的学生人数. -
11、如图,在∠ABC中,AB=BC,AC=4,tan∠BAC=
 (1)、尺规作图:在图中作出以AC为对角线的菱形ABCD(保留作图痕迹,不用说明作图过程);(2)、求(1)中所作菱形ABCD的面积.
(1)、尺规作图:在图中作出以AC为对角线的菱形ABCD(保留作图痕迹,不用说明作图过程);(2)、求(1)中所作菱形ABCD的面积. -
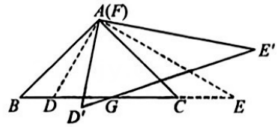
12、如图,直角三角形纸片DEF叠放在直角三角形纸片ABC上,直角顶点A,F重合,顶点B,D,C,E在同一直线上。现将纸片DEF绕点F旋转,顶点D,E旋转后的对应点分别记为D',E',边D'E'与边BC的交点为G.若∠ABC=45°,∠FED=30°,BC=12 cm,GC=5cm,则GE'=cm.
-
13、关于x的一元二次方程x2+bx+c=0的两个非零实数根分别是m和2m,则.
-
14、 如图,PA,PB分别与⊙O相切于点A,B,点D在上(不与点A,B重合),若∠P=100°,则∠D=°.

-
15、一个不透明的口袋中有2个红球和3个白球,它们除颜色外无其他差别,从口袋里随机摸出1个球,摸到白球的概率为.
-
16、若分式的值等于1,则x=.
-
17、在菱形ABCD中,∠A为锐角,点M,N分别在边AB,BC上,连结DM,DN,则下列四个命题中,假命题为( )A、若 AM=CN,则DM=DN B、若∠BMD=∠BND,则DM=DN C、若AM=BN,则DM=DN D、若∠MDN=∠A,则DM=DN
-
18、某早餐店每天都要采购豆奶、牛奶和果汁三种饮品,其中豆奶瓶数是牛奶瓶数的2倍,豆奶、牛奶的采购价分别为2元/瓶、5元/瓶.若采购的总费用只与三种饮品的总瓶数有关,与三种饮品的瓶数比例变化无关,则果汁的采购价为( )A、2元/瓶 B、3元/瓶 C、5元/瓶 D、7元/瓶
-
19、 若点 , , 都在反比例函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、
-
20、 如图,在矩形 ABCD 中, 的平分线交边 BC 于点 E,ED 恰好平分 . 若 , 则 的面积为( )
 A、2 B、 C、4 D、
A、2 B、 C、4 D、