相关试卷

1、计算： $|- \sqrt{3}| + {(\frac{1}{5})}^{- 1} + {(π + 2025)}^{0} + \tan 45 °$ ．

查看解析
2、美术课上，聪聪用一块边长为2的正方形的厚纸板，做了一套七巧板（如图①）．慧慧用聪聪做的七巧板拼成了如图②所示的美术作品，则图中 $\tan ∠ A B C =$ ．

查看解析
3、如图，已知四边形 $A B C D$ 是平行四边形，分别以点A，B为圆心，以大于 $\frac{1}{2} A B$ 长为半径画弧，两弧相交于点E，F，过E，F两点作直线恰好经过点D，交对角线 $A C$ 于点O，若 $A C = 9$ ，则 $A O$ 的长为．

查看解析
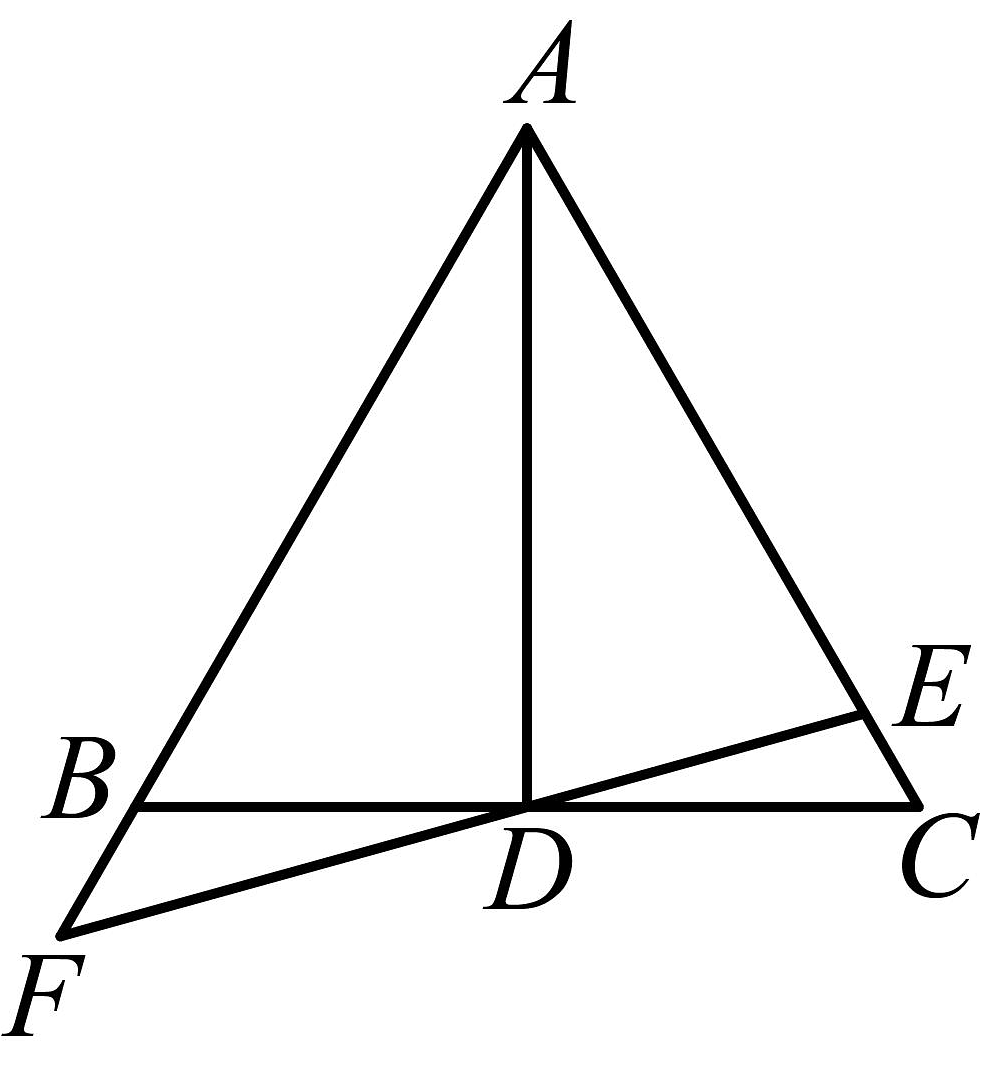
4、如图， $△ A B C$ 为等边三角形，点D是 $B C$ 边的中点，过点D的直线与 $A C$ 相交于点E，与 $A B$ 的延长线相交于点F，当 $A E = A D$ 时，则 $∠ F =$ ．

查看解析
5、如图，矩形 $A B C D$ 中，边 $A B$ 长为x，边 $A D$ 长为y，矩形的面积为8，则y关于x的函数关系式为．

查看解析
6、已知关于x的一元二次方程 $x^{2} - 4 x + 2 a = 0$ 有两个不相等的实数根，则a的取值范围是．

查看解析
7、《共和国的数学家》丛书含陈景润等五位数学家的分册．书包中有如图所示的五本书，随机抽取一本是《共和国的数学家—陈景润》的概率是．

查看解析
8、《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数．若收入300元，记作 $+ 300$ 元，则 $- 200$ 元表示．

查看解析
9、定义：若一个整数能表示成 $a^{2} + b^{2}$ （ $a ， b$ 是整数）的形式，则称这个数为“和谐数”．例如， $13 = 3^{2} + 2^{2}$ ，所以13是“和谐数”．下列说法不正确的是（）

A、34是和谐数 B、 $a^{2} + 2 a b + 2 b^{2}$ （ $a ， b$ 是整数）不一定是和谐数 C、如果数 $m ， n$ 都是“和谐数”（ $m \neq n$ ），则 $\frac{{(m + n)}^{2} - {(m - n)}^{2}}{4}$ 也是“和谐数” D、当 $k = 13$ 时， $x^{2} + 4 y^{2} + 4 x - 12 y + k$ （ $x ， y$ 是整数）是“和谐数”

查看解析
10、如图，点A，B，C，D在 $⊙ O$ 上，且四边形 $A B C O$ 是菱形，则 $∠ D$ 的大小为（）

A、 $30 °$ B、 $35 °$ C、 $40 °$ D、 $45 °$

查看解析
11、为“有效减少近视发生，呵护孩子光明未来”，某班体育委员将全班50名同学视力检查数据，绘制成了如图所示的条形统计图，则这50名同学视力检查数据的中位数和众数分别是（）

A、4.8，13 B、4.7，4.8 C、13，4.8 D、4.8，4.8

查看解析
12、如图，四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点O，已知 $A D ∥ B C$ ，若要证明四边形 $A B C D$ 为平行四边形，则还需要添加一个条件是（）

A、 $A B = B C$ B、 $O A = O B$ C、 $A D = B C$ D、 $A C ⊥ B D$

查看解析
13、计算 $\sqrt{12} \div \sqrt{3}$ 的结果是（）

A、4 B、2 C、3 D、 $\sqrt{2}$

查看解析
14、若代数式 $\frac{2025}{x - 1}$ 有意义，则x的取值范围是（）

A、 $x > 1$ B、 $x \geq 1$ C、 $x < 1$ D、 $x \neq 1$

查看解析
15、由5个相同的小立方体搭成的物体如图所示，则它的左视图为（）

A、 B、 C、 D、

查看解析
16、在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ 与x轴交于 $A (- 1, 0)$ ， $B (3, 0)$ 两点，与y轴交于C点，设抛物线的对称轴为直线l．

(1)、求抛物线的解析式；

(2)、如图（甲），设点C关于直线l的对称点为点D，在直线l上是否存在一点P，使 $P A - P D$ 有最大值？若存在，求出 $P A - P D$ 的最大值；若不存在，请说明理由；

(3)、如图（乙），设点M为抛物线上一点，连接 $M C$ ，过点M作 $M N ⊥ C M$ 交直线l于点N．若 $\tan ∠ M C N = \frac{2}{3}$ ，求点M的坐标．

查看解析
17、如图， $A B$ 是 $⊙ O$ 的直径，C，D是 $⊙ O$ 上两点，连接 $A C$ ， $B C$ ， $C O$ 平分 $∠ A C D$ ， $C E ⊥ D B$ ，交 $D B$ 延长线于点E．

(1)、求证： $C E$ 是 $⊙ O$ 的切线；

(2)、若 $⊙ O$ 的半径为5， $\sin D = \frac{3}{5}$ ，求 $B D$ 的长．

查看解析
18、在数学综合实践活动中，次仁和格桑自主设计了“测量家附近的一座小山高度”的探究作业．如图，次仁在A处测得山顶C的仰角为 $30 °$ ；格桑在B处测得山顶C的仰角为 $45 °$ ．已知两人所处位置的水平距离 $M N = 210$ 米，A处距地面的垂直高度 $A M = 30$ 米，B处距地面的垂直高度 $B N = 20$ 米，点M，F，N在同一条直线上，求小山 $C F$ 的高度．（结果保留根号）

查看解析
19、先化简，再求值： $(1 + \frac{2}{m - 2}) \cdot \frac{m^{2} - 4}{m}$ ，请为m选择一个合适的数代入求值．

查看解析
20、如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ，以点B为圆心，适当长为半径作弧，分别交 $B C$ ， $B A$ 于点D，E，再分别以点D，E为圆心，大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ A B C$ 的内部相交于点P，作射线 $B P$ 交 $A C$ 于点F．已知 $C F = 3$ ， $A F = 5$ ，则 $B F$ 的长为．

查看解析

上一页 306 307 308 309 310 下一页跳转