-
1、 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递40件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件x件,根据题意可列方程为( )A、 B、 C、 D、
-
2、如果代数式x2-2x+5的值为3,那么代数式2x-x2的值等于( )A、2 B、-2 C、8 D、-8
-
3、如果x<y,那么下列不等式正确的是( )A、3x<3y B、-2x<-2y C、x+2>y+2 D、x-1>y-1
-
4、 随着科学技术的不断发展,5G网络已经成为新时代的“宠儿”,截至2024年11月,我国5G移动电话用户达10.02亿户,将10.02亿用科学记数法可表示为( )A、 B、 C、 D、
-
5、如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
6、如果高于海平面100m记作+100m,那么低于海平面50m应该记作( )A、+50m B、-50m C、m D、-100m
-
7、如图,在中,直径于点 , 连结并延长交于点 , 点为上一点,且 .
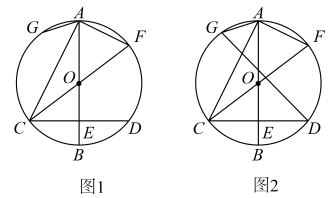 (1)、求的度数.(2)、求证: .(3)、连结 , 如图 , 若 , 求的值.
(1)、求的度数.(2)、求证: .(3)、连结 , 如图 , 若 , 求的值. -
8、在平面直角坐标系中,已知抛物线经过点 .(1)、请用含的代数式表示 .(2)、若该抛物线向上平移个单位后顶点恰好落在轴上,求该抛物线的函数表达式.(3)、已知和是该抛物线上的两点.若对于 , , 都有 , 求的取值范围.
-
9、某款电热水壶有两种工作模式:煮沸模式和保温模式.在煮沸模式下将水加热后自动进入保温模式.现有一壶的水经过分钟烧至后进入保温模式,数学实验小组对这一过程进行了观察与记录,并绘制出水温与时间分的关系如图所示.
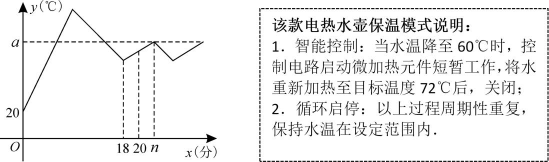 (1)、求的值为.(2)、已知时, , 求当时水温与时间之间的函数关系式,并求出的值.(3)、当时,求此时电热水壶中水的温度是多少 .
(1)、求的值为.(2)、已知时, , 求当时水温与时间之间的函数关系式,并求出的值.(3)、当时,求此时电热水壶中水的温度是多少 . -
10、某校九年级学生共人,为了解九年级学生的体能情况,从中随机抽取部分学生进行分钟的跳绳测试,小慧将这次测试结果的数据分成组绘成如图所示频数直方图,并发现跳绳次数不少于次的同学占 , 第 , 两组频率之和为 , 且第组与第组的频数都是 , 第 , , 组频数之比为 .
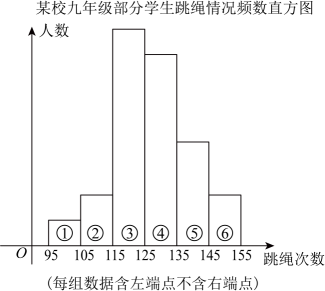
根据小慧提供的材料,请解答如下问题:
(1)、这次跳绳测试共抽取多少名学生?(2)、第组的频数与频率分别是多少?(3)、现学校计划表彰前的学生,请结合频数直方图确定被表彰学生的分钟跳绳次数,并说明理由. -
11、如图,在中, , , .
 (1)、利用直尺和圆规在上取一点 , 使得 , 保留作图痕迹.(2)、求的面积.
(1)、利用直尺和圆规在上取一点 , 使得 , 保留作图痕迹.(2)、求的面积. -
12、如图,已知 , , , 在同一条直线上, , , , 与交于点 .
 (1)、求证: .(2)、若 , , 求的度数.
(1)、求证: .(2)、若 , , 求的度数. -
13、解方程组: .
-
14、计算: .
-
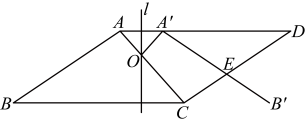
15、如图,在中,为对角线上一点,且 , 线段与线段关于过点的直线对称,点的对应点在线段上, , 与相交于点 , 连接 , 则四边形与的面积之比为 .
-
16、如图,在中,垂直平分 , 点 , 分别是 , 的中点,连结 , 交于 , 延长交于点若 , 则的长为 .

-
17、不透明袋子中装有个球,其中有个红球、个绿球、个蓝球,这些球除颜色外无其他差别.从袋子中随机取出个球,则它是蓝球的概率是 .
-
18、如图,是的弦,与相切于点 , 经过圆心.若 , 则 .

-
19、分解因式: .
-
20、如图,是边长为的正三角形,点 , 分别是边 , 上的动点,连结 , 交于点 , 且作于点 , 于点下列两条线段的和,不随 , 的运动而改变的是( )
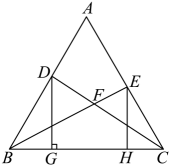 A、 B、 C、 D、
A、 B、 C、 D、