-
1、已知反比例函数的图像上有 , 两点,下列说法正确的是( )A、当时, B、当时, C、当时, D、当时,
-
2、如图是由个全等的直角三角形和一个小正方形组成的大正方形.若 , , 则直角的面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、不等式组的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
4、小聪在活动课上做“小孔成像”实验,如图所示,若 , , 蜡烛火焰倒立像 , 则下列说法中,错误的是( )
 A、蜡烛火焰和蜡烛火焰倒立像可以看成是位似图形 B、 C、蜡烛火焰长 D、线段中点与线段中点的连线不一定经过点
A、蜡烛火焰和蜡烛火焰倒立像可以看成是位似图形 B、 C、蜡烛火焰长 D、线段中点与线段中点的连线不一定经过点 -
5、某校名同学在歌唱比赛中的成绩单位:分分别为 , , , , , 这组数据的中位数是( )A、 B、 C、 D、
-
6、下列运算结果正确的是( )A、 B、 C、 D、
-
7、下列图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
8、年,我市消费品以旧换新居家适老化改造申请户,完成改造户,完成系统审价补贴金额达元,数字用科学记数法表示为( )A、 B、 C、 D、
-
9、分解因式: .
-
10、数学活动课上,老师准备了若干个如图(1)的三种纸片.甲种纸片是边长为a的正方形,乙种纸片是边长为b的正方形,丙种纸片是长为b、宽为a的长方形.

【观察发现】
用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成如图(2)的大正方形.观察图(2)的面积关系,写出正确的等式:________________.
【操作探究】
若要拼出一个面积为的长方形,则需要甲种纸片________张,乙种纸片________张,丙种纸片________张.(所拼图形不重叠无缝隙)
【拓展延伸】
两个正方形、如图(3)摆放,边长分别为x,y,连接 , . 若 , , 求图中阴影部分的面积.
-
11、如图, , , , 将求的过程填写完整.

解:∵ . ( 已知)
∴ . ( ▲ )
又∵( 已知)
∴ . ( ▲ )
∴ . ( ▲ )
∴ . ( ▲ )
又∵ . ( 已知)
∴ ▲ . (等式的性质)
-
12、阅读材料:如果一个数的平方等于 , 规定 , 这个数i叫做虚数单位,那么形如(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部.
它有如下特点:
①它的加,减,乘法运算与整式的加,减,乘法运算类似,例如计算:
; .
②若两个复数,它们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚部互为相反数,则称这两个复数共轭;如的共轭复数为 .
(1)、填空:①;②;(2)、若是的共轭复数,求的值; -
13、如图,直线a、b相交于点O,将量角器的中心与点O重合,表示的点在直线b上,则 .
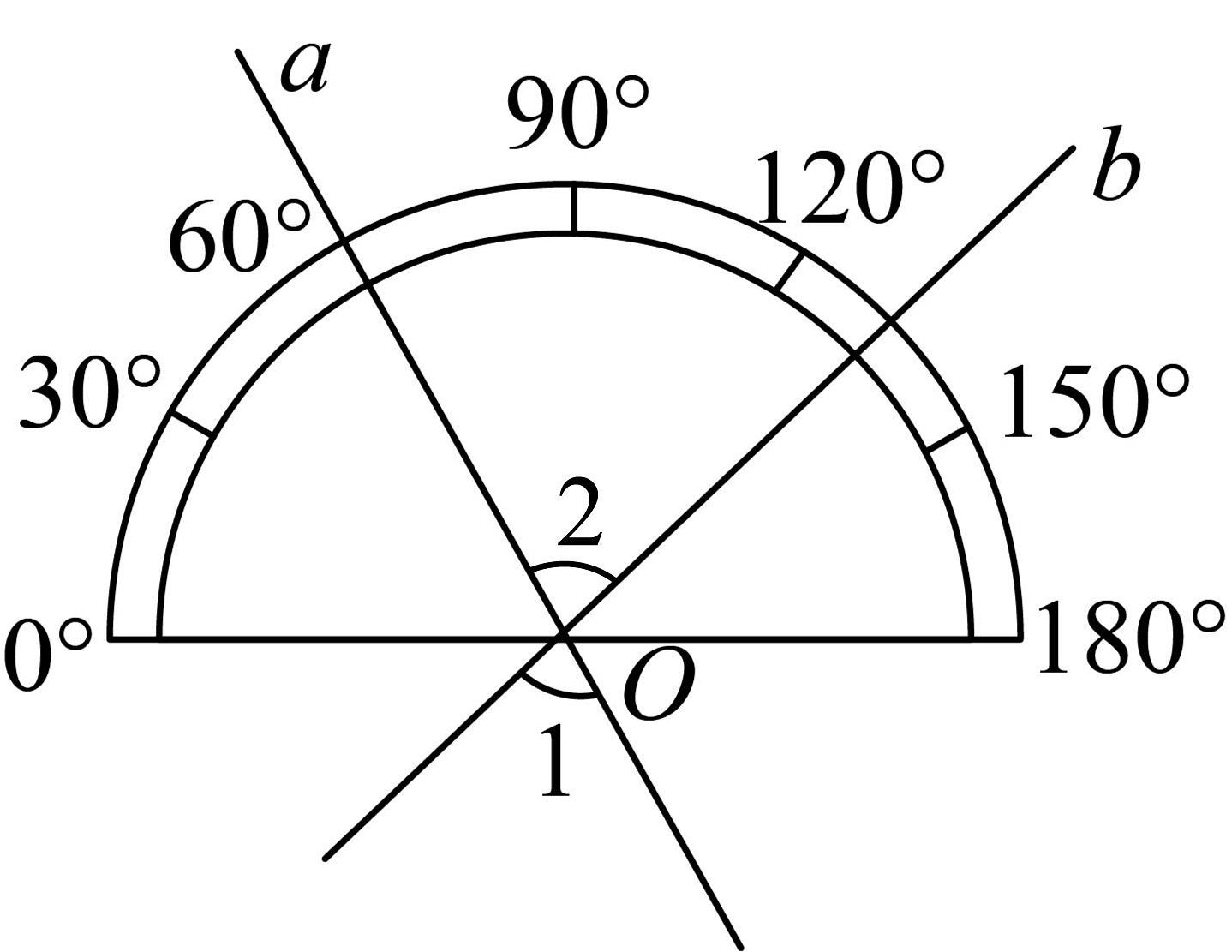
-
14、如图1,在矩形中, , P是线段上一个动点(P不与A重合),以为边在的上方作正方形 , 连接 , , , 与交于点G.
 (1)、若正方形和矩形的周长相等,则的值为__________;(2)、若 , 当长为多少时,是直角三角形?请说明理由;(3)、把图1沿折叠,点F恰好落在线段的延长线上的点处,如图2所示,求的值.
(1)、若正方形和矩形的周长相等,则的值为__________;(2)、若 , 当长为多少时,是直角三角形?请说明理由;(3)、把图1沿折叠,点F恰好落在线段的延长线上的点处,如图2所示,求的值. -
15、已知:如图1,二次函数与x轴相交于A,两点,与y轴交于点C,连接 , P是第一象限的抛物线上一点.
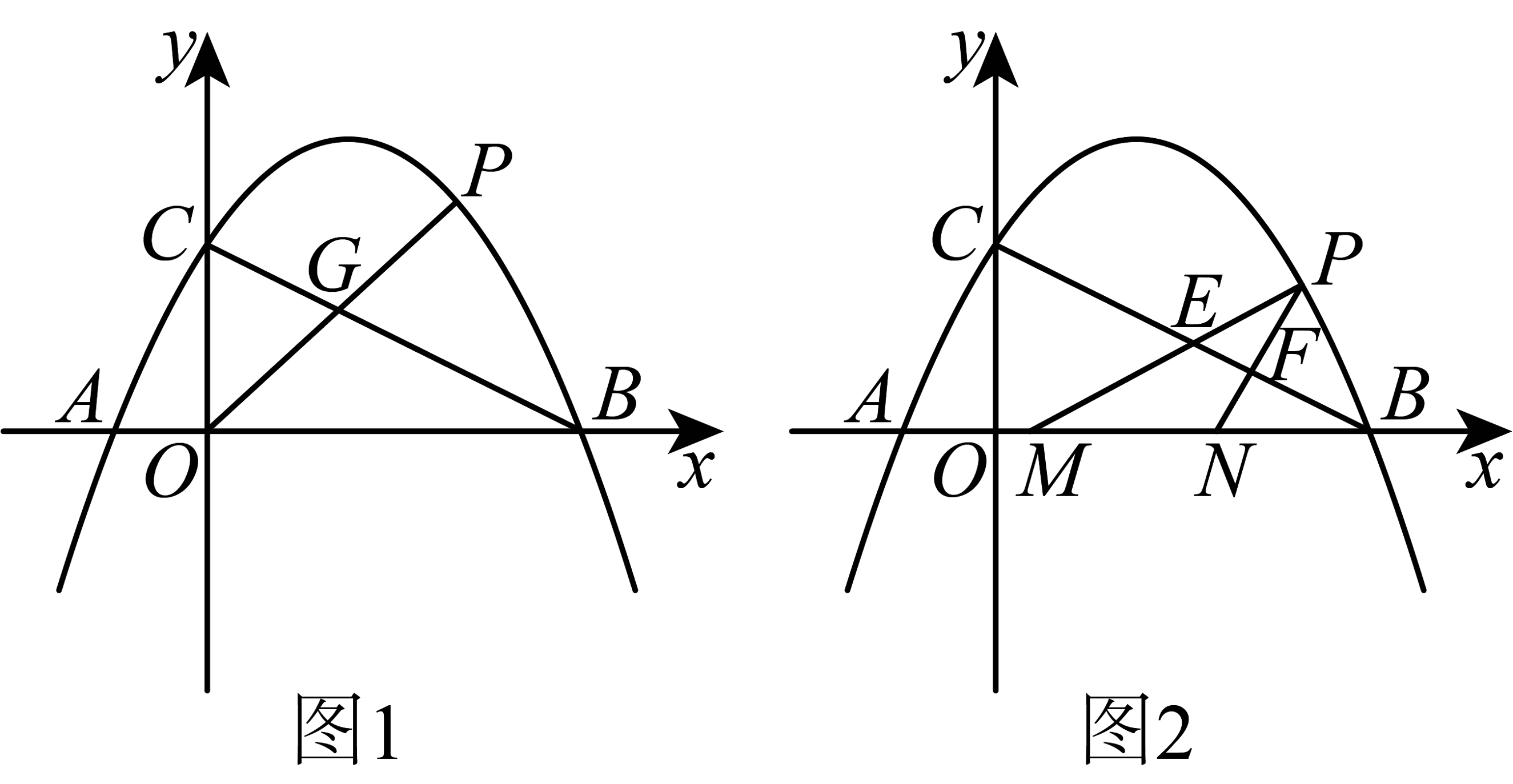 (1)、求二次函数和直线的表达式;(2)、连接与交于点G,若 , 求点P的坐标;(3)、如图2,已知M,N是x轴上点B左侧(N不与B重合)两个动点,M在N的左边, , 连接交于点E,连接交于点F,求的最小值.
(1)、求二次函数和直线的表达式;(2)、连接与交于点G,若 , 求点P的坐标;(3)、如图2,已知M,N是x轴上点B左侧(N不与B重合)两个动点,M在N的左边, , 连接交于点E,连接交于点F,求的最小值. -
16、如图所示,菱形的顶点A,B,D都在上,延长交于点E,连接 .
 (1)、求证:是等腰三角形;(2)、已知菱形的边长为3, , 求四边形的面积.
(1)、求证:是等腰三角形;(2)、已知菱形的边长为3, , 求四边形的面积. -
17、【问题背景】2025年某市将迎来“第四届天门山跑酷大赛”,筹备委员会要在“云纵天梯”上设置108组障碍道具,但需要知道天梯最后一段AB的长度,某数学兴趣小组在老师的指导下进行了测量活动.
【实施过程】
活动主题
测量天门山云纵天梯的长度
测量工具
皮尺、测角仪、计算器等
活动过程
模型
抽象

测绘过程
与数据信息
设台阶的起点为B,终点为A,B在水平直线l上,线段和直线l在同一平面内,点A的铅垂高于点C.已知台阶的坡度①从点B开始沿的延长线方向行走44米到达点D处,在D处测得点A的仰角为;②用计算器计算得: , , , , , .
【问题解决】
请根据表格中提供的信息,解决下列问题:
(1)、求天梯的坡角的度数;(2)、求天梯的长度是多少米.(结果精确到整数) -
18、某小区在小区内安装垃圾分类的A型固定垃圾箱和B型移动垃圾箱,已知购买3个A型固定垃圾箱和2个B型移动垃圾箱共需560元,1个A型固定垃圾箱和1个B型移动垃圾箱共需200元.(1)、求A型固定垃圾箱和B型移动垃圾箱的单价各是多少元;(2)、如果需要购买A型固定垃圾箱和B型移动垃圾箱共90个,且费用不超过6000元,问:那该小区最多可以购买A型固定垃圾箱多少个?
-
19、某学校准备开设“A.编织;B.厨艺;C.电工;D.园艺”四种类别的劳动课,为了了解学生对劳动课类别的选择意向(每个同学只能选择其中一项),随机抽取了部分同学进行调查,并将调查结果绘制出如图所示的不完整的统计图.
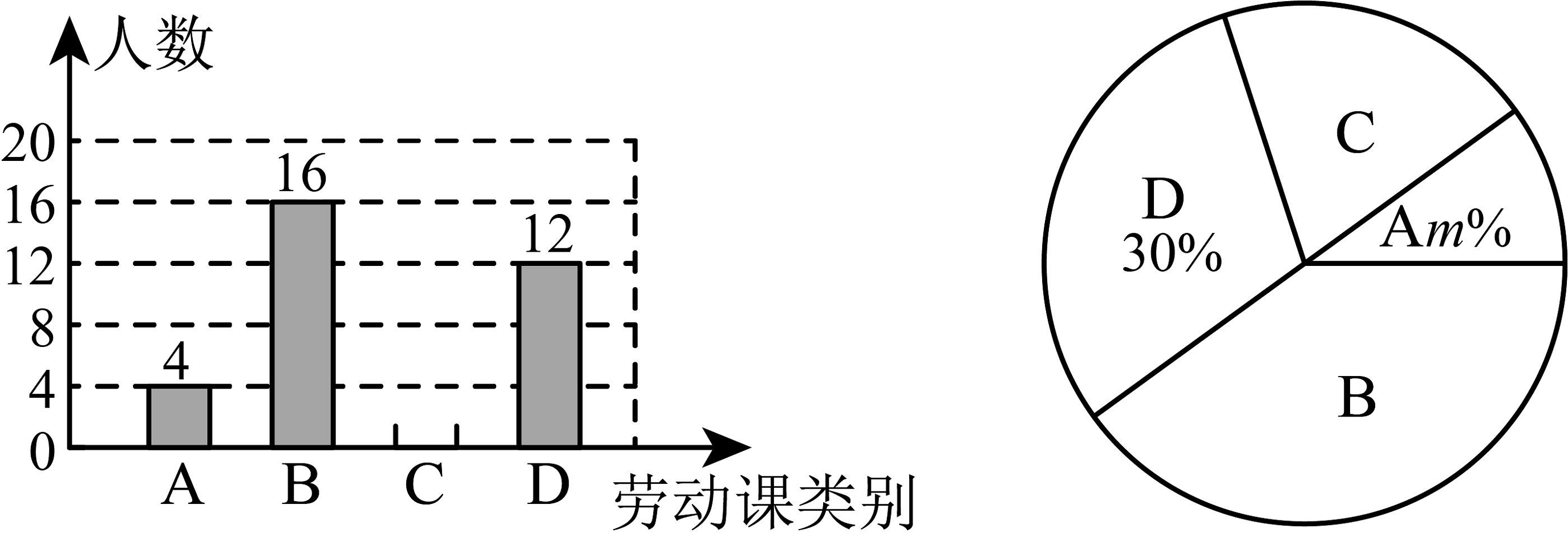
请结合图中的信息解答下列问题:
(1)、本次共调查了__________名学生,扇形统计图中m的值为__________;(2)、将条形统计图补充完整;C组所对应的扇形圆心角为__________;(3)、若该校共有学生1200人,则估计该校喜欢厨艺的学生人数为多少? -
20、先化简,再求值: , 其中 .