-
1、已知点都在反比例函数的图象上,若 , 则、、的大小关系(用“<”连接).
-
2、若一次函数的图象不经过第三象限,则的取值范围是 .
-
3、如图,在平面直角坐标系中,为直角三角形,轴于点 , 点在第一象限,为斜边上一点,且 , 过点作(点在直线的右侧),已知 , 点在反比例函数的图象上,反比例函数的图象过点 . 结合图象判断下列结论:①;②四边形是平行四边形;③点是的中点;④的值是2.其中正确结论有( )
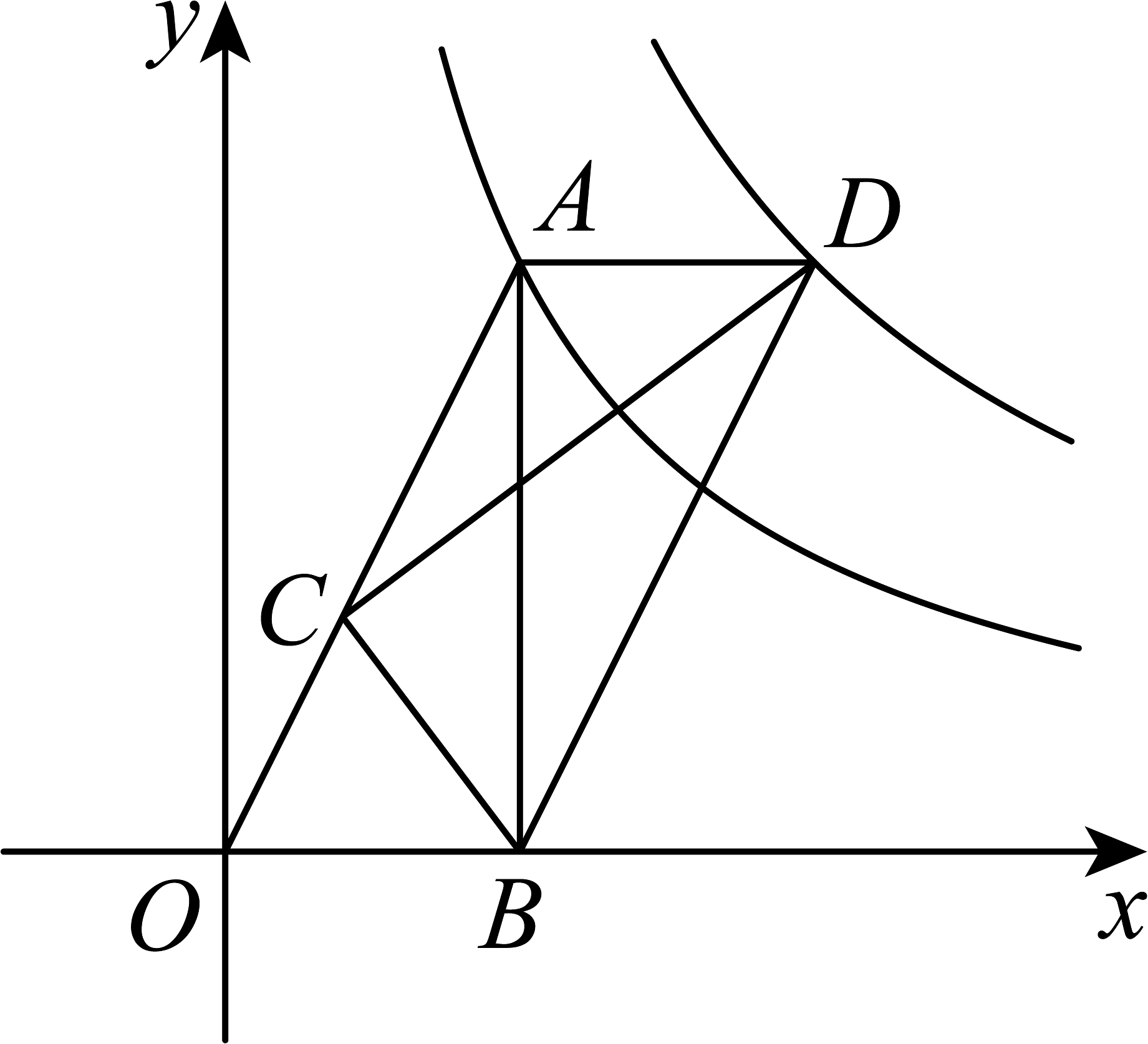 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
4、综合实践课上,李海画出 , 利用尺规作图找一点 , 使得四边形为平行四边形.图图③是他的作图过程.
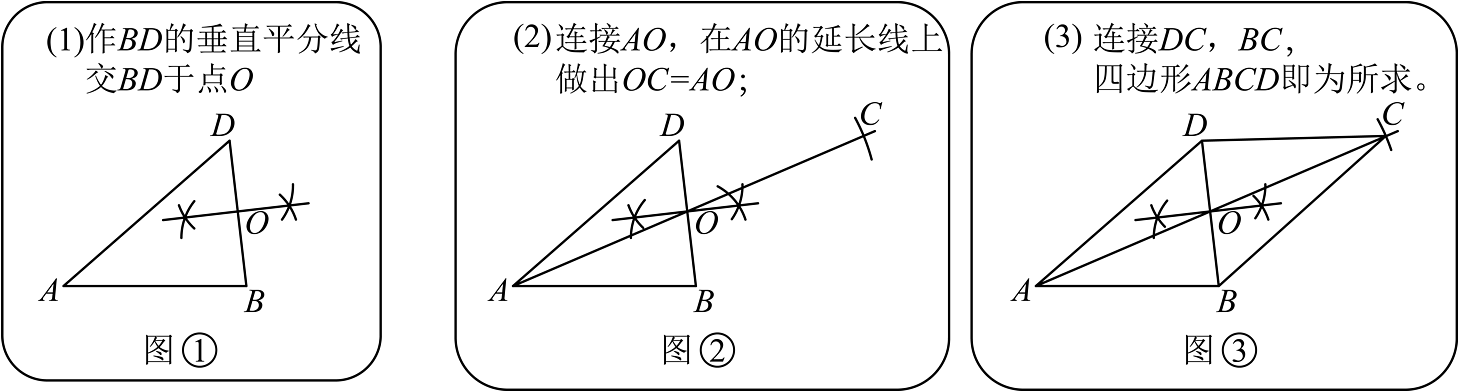
李海的作法中,可直接判定四边形是平行四边形的条件是( )
A、两组对边分别平行 B、两组对边分别相等 C、对角线互相平分 D、一组对边平行且相等 -
5、如图,已知 , 添加下列条件可以使四边形成为平行四边形的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、如图表示的是一次函数(、为常数,)的图象,则关于的方程的解是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
8、中国的k在网上成为热搜和下载安装的榜首软件,要支持这些软件功能,需要芯片的支持.据报道的主要芯片为 , 相当于 , 数据用科学记数法表示为( )A、 B、 C、 D、
-
9、下列各式中是分式的是( )A、 B、 C、 D、
-
10、如图1,是的直径,是左半圆上的任意一点(不与 , 重合),是劣弧上一动点.连结 , , 在右半圆上取一点 , 使得 , 连接并交于点 .
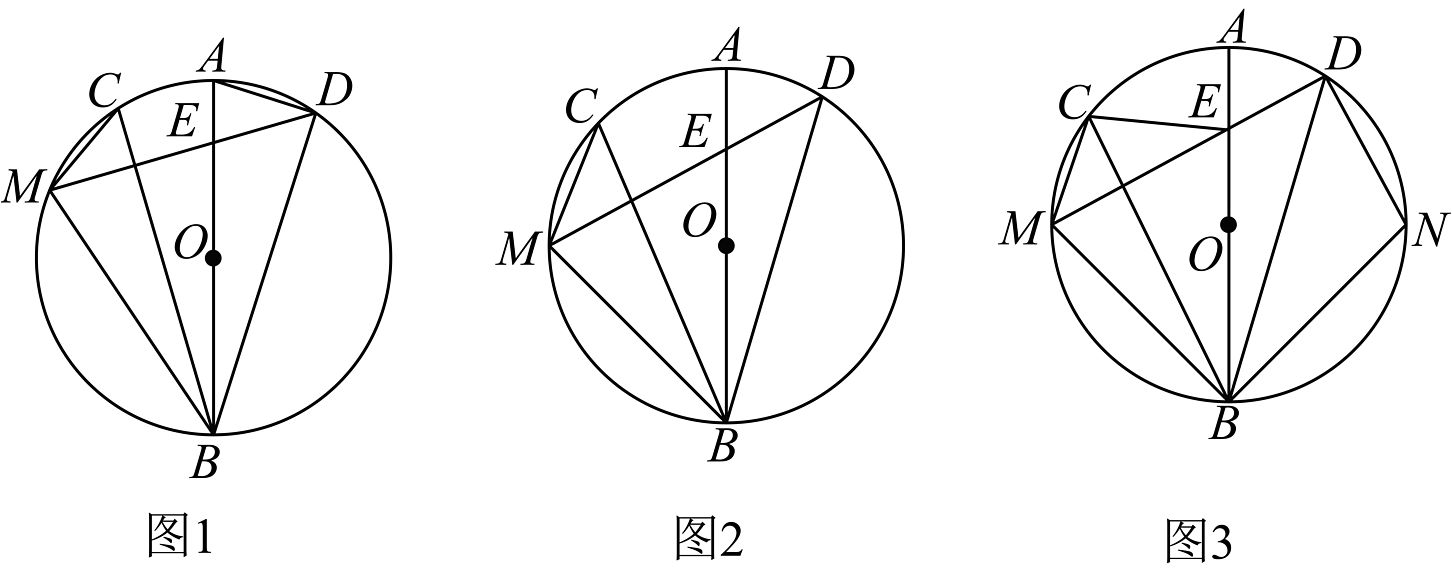 (1)、求证:(2)、如图2,当为左半圆上的中点时,求证:在点运动过程中,始终存在 .(3)、如图3,在(2)的条件下,连结 , 取右半圆中点 , 连结 , , 求证:与面积相等
(1)、求证:(2)、如图2,当为左半圆上的中点时,求证:在点运动过程中,始终存在 .(3)、如图3,在(2)的条件下,连结 , 取右半圆中点 , 连结 , , 求证:与面积相等 -
11、在平面直角坐标系中,点 , 点在抛物线上.设抛物线的对称轴为直线 .(1)、当时,
①直接写出与满足的等量关系;
②比较 , 的大小,并说明理由;
(2)、已知点在该抛物线上,若对于 , 都有 , 求的取值范围. -
12、如图,在锐角三角形中, . 以点为圆心,长为半径画弧,交边于点 , 连结 , 点是延长线上的一点,连结 , 若平分 .
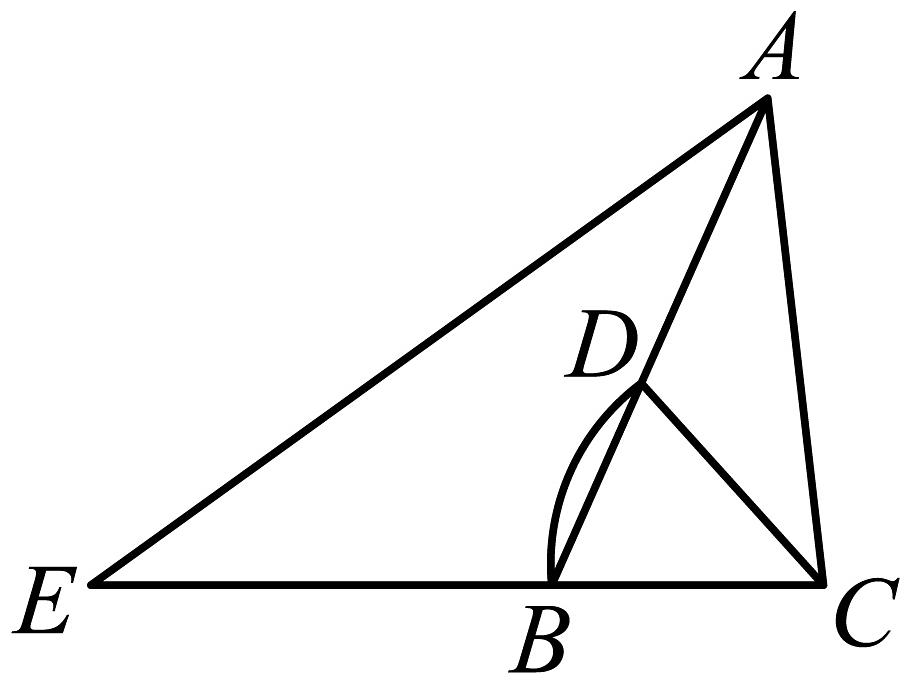 (1)、求证:;(2)、当 , 求的值.
(1)、求证:;(2)、当 , 求的值. -
13、解方程组:
-
14、计算: .
-
15、如图,的半径为2,现将含的直角三角板中的角的顶点在圆弧上进行滑动,并始终保持斜边和长直角边与圆弧相交于点和点 , 并作交的延长线于点 , 则的最大面积是

-
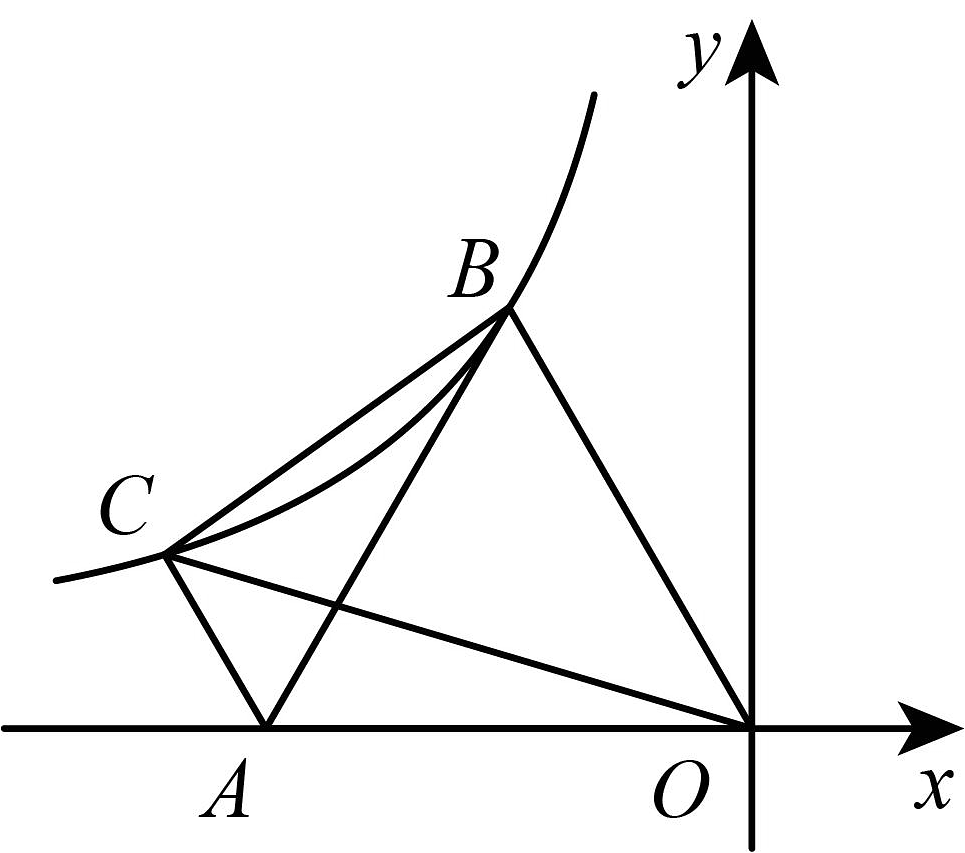
16、如图,在平面直角坐标系中,为坐标原点,点为轴上的一点,将绕点按顺时针旋转至 , 反比例函数的图象经过点 , 过作交反比例函数图象于点 , 若的面积为 , 则的值为
-
17、如图,在中, , 于点 , 若 , 则 .

-
18、当时,则 .
-
19、一个不透明的口袋中装有红色、黄色、蓝色玻璃球共200个,这些球除颜色外都相同,小明通过大量随机摸球试验后,发现摸到红球的频率稳定在0.2左右,则可估计红球的个数约为.
-
20、将多项式因式分解得 .