-
1、年蛇年春晚主标识是基于甲骨文的“巳”字进行创作的,将两个“巳”对称放在一起组成“巳巳如意纹”,经二方连续、四方连续展现出无限可能,象征着生生不息.下列是相关图案,其文字上方的图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2、如图,等边的边长为6,为边上一点,于点 .
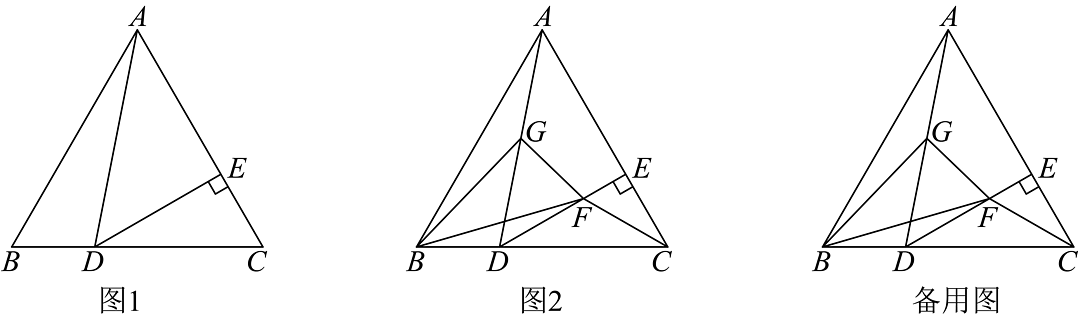
【初步感知】(1)如图1,若 , 求的长.
【深入探究】(2)如图2,线段的垂直平分线交于点 , 点为的中点,连接 , 求证: .
【拓展延伸】(3)在(2)的条件下,若 , 求与之间的关系.
-
3、综合与实践
【主题】运动场设计
【素材】某中学为迎接运动会,计划翻新校园田径场,原场地为半圆式跑道(如图),直道长度米,弯道为半圆形,最内侧跑道(第1道)弯道半径米,共8条跑道,每条跑道宽1.22米.(其中跑道半径按内径计算,)

【实践探究】
(1)、计算验证第1道跑道是否符合标准跑道要求(第一圈跑道不能小于).(结果保留2位小数)(2)、体育组发现:当所有跑道起点、终点均为同一条直线时(如图),第6道运动员跑完2圈时,电子计步器显示实际跑动距离为 . 请结合跑道结构图解释此现象. -
4、某数学兴趣小组想要利用所学的知识测量某栋大楼的高度,记录如下:
课题
测量大楼的高度
活动方案
方案一
方案二
测量方案示意图


实施方案
1、选取与大楼底部位于同一水平地面的处;
2、在处,测量大楼顶部的仰角;
3、沿着方向走至处,测量大楼顶部处的仰角;
4、测量、之间的距离.
1、选取大楼旁的建筑物;
2、在处,测量大楼顶部处的仰角;
3、在处,测量大楼底部处的俯角;
4、测量大楼与建筑物之间的距离 .
测量数据
, ,
, ,
备注
1、图上所有点均在同一平面;
2、 , , ,
1、图上所有点均在同一平面;
2、 , , , , ,
请选择其中一个方案及其测量数据求出大楼的高度 . (结果精确到)
-
5、计算: .
-
6、如图,在中, , , , 点D、E分别是 , 上的动点,且 , 连接 , , 则的最小值是 .
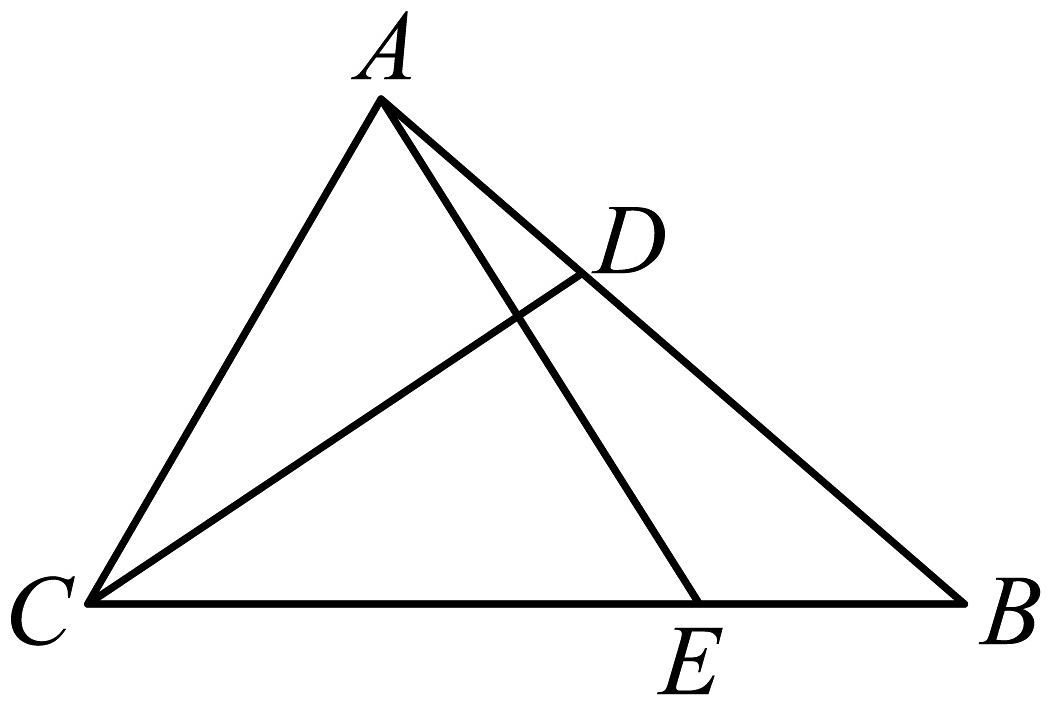
-
7、使函数有意义的自变量的取值范围叫做函数的定义域,则函数的定义域为 .
-
8、如图,在平面直角坐标系中,直线与双曲线交于A、B两点,P是以点为圆心,半径长为1的圆上一动点,连接AP,M为AP的中点.则线段OM长度最大值为( )
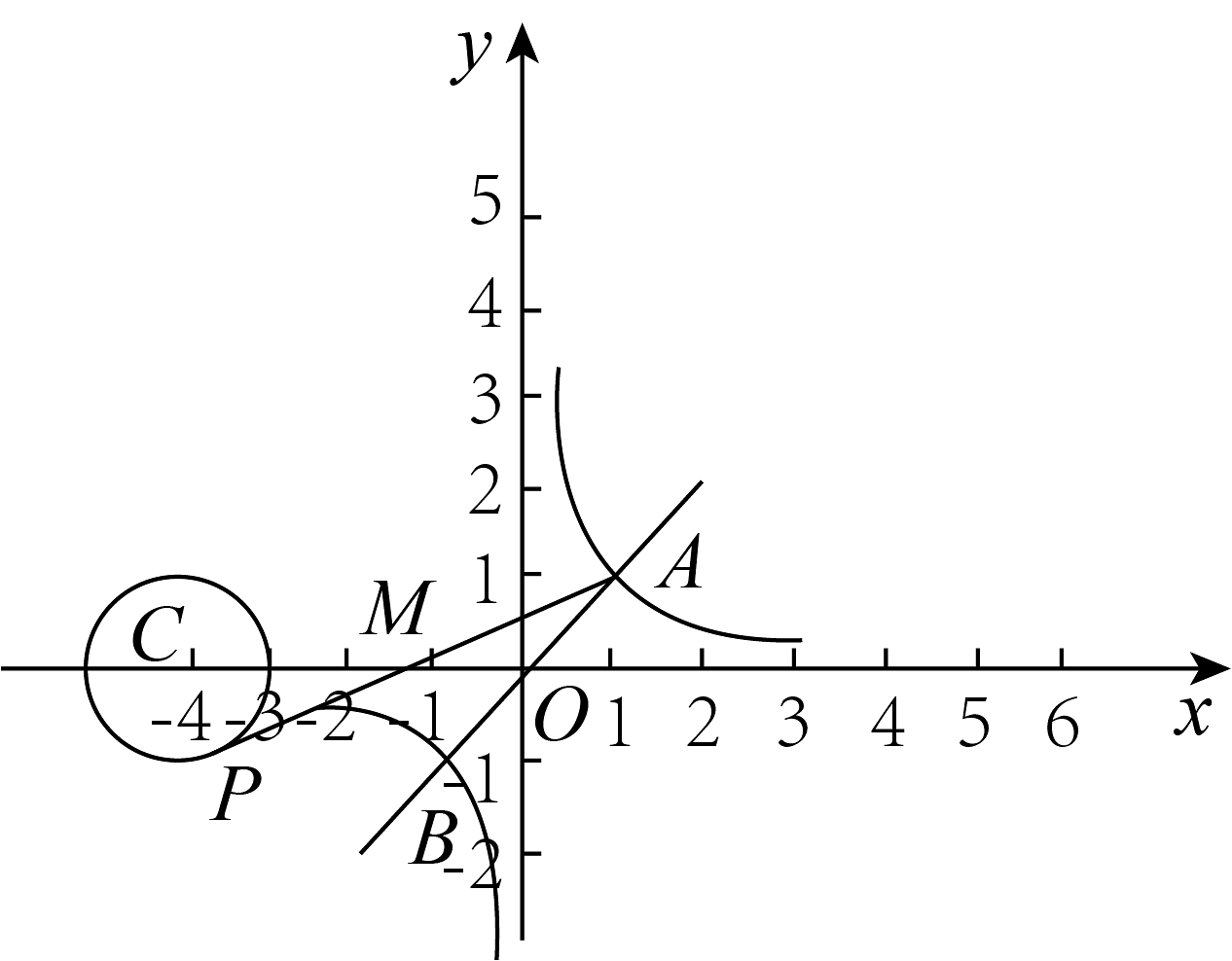 A、2 B、1 C、 D、
A、2 B、1 C、 D、 -
9、我们知道,引进了无理数后,有理数集就扩展到实数集.同样,如果引进“虚数”,则实数集就扩展到“复数集”.现在我们定义:虚数单位“”,其运算规则是: , , , , , , , 则的值是( )A、 B、 C、 D、
-
10、关于二次函数的最大值或最小值,下列说法正确的是( )A、有最大值3 B、有最小值3 C、有最大值6 D、有最小值6
-
11、如图,在中, , 点在直线上.若 , , 则的度数为( )
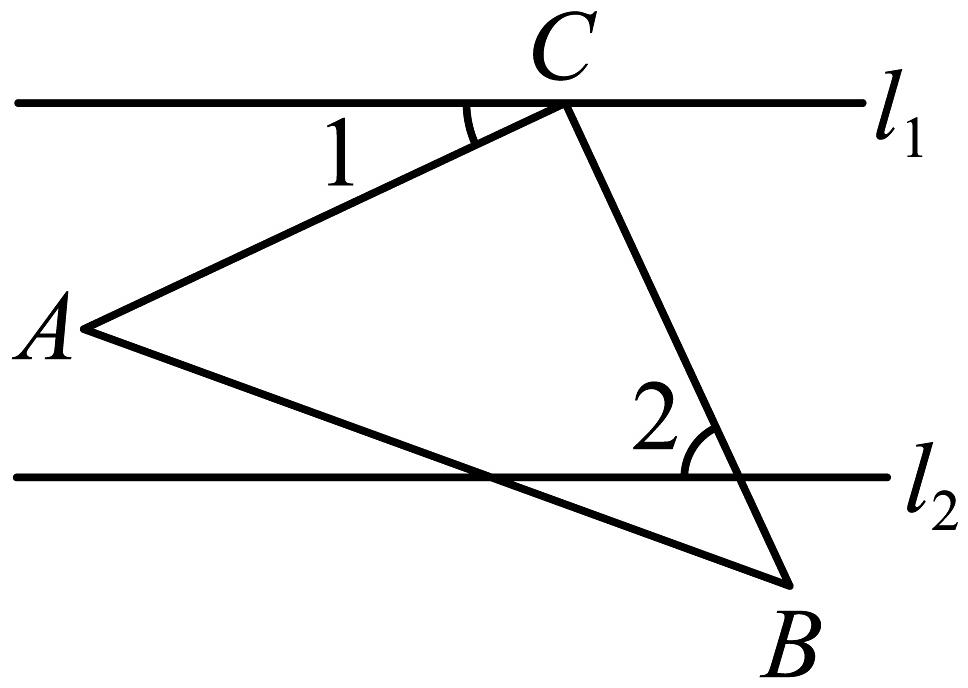 A、 B、 C、 D、
A、 B、 C、 D、 -
12、从“我命由我不由天”这句话中随机选取一个汉字,选取“我”字的概率是( )A、 B、 C、 D、
-
13、把分解因式,结果正确的是( )A、 B、 C、 D、
-
14、已知直线经过点 , 则的值等于( )A、5 B、 C、7 D、
-
15、下列实数中,最小的数是( )A、 B、0 C、 D、
-
16、如图1,是的外接圆,是的直径,点是上一点,连接交于点 , 过点作 , 交于点 , 交的延长线于点 .
 (1)、求证:;(2)、如图2,连接 ,
(1)、求证:;(2)、如图2,连接 ,
①若 , , 求的长度;
②如图3,若点是的中点,过点作交的延长线于点 ,
求证: .

-
17、在平面直角坐标系中,抛物线:与x轴交于 , B两点,与y轴交于点C.(1)、求b的值;(2)、如图1,点P是直线上方抛物线上一点,横坐标设为m,且 . 连接 , 交于点D, .

①求点P的坐标;
②如图2,将抛物线沿x轴向右平移3个单位,得到抛物线 , 点F为点P平移后的对应点,连接交y轴于点M.点N为抛物线上任意一点,连接 . 若 , 求线段的长.

-
18、综合与实践
目标
篮球架安装是否合格及测量伸臂距离地面的高度
工具
测角仪、卷尺
素材1
小敏借助测角仪测得: , , .
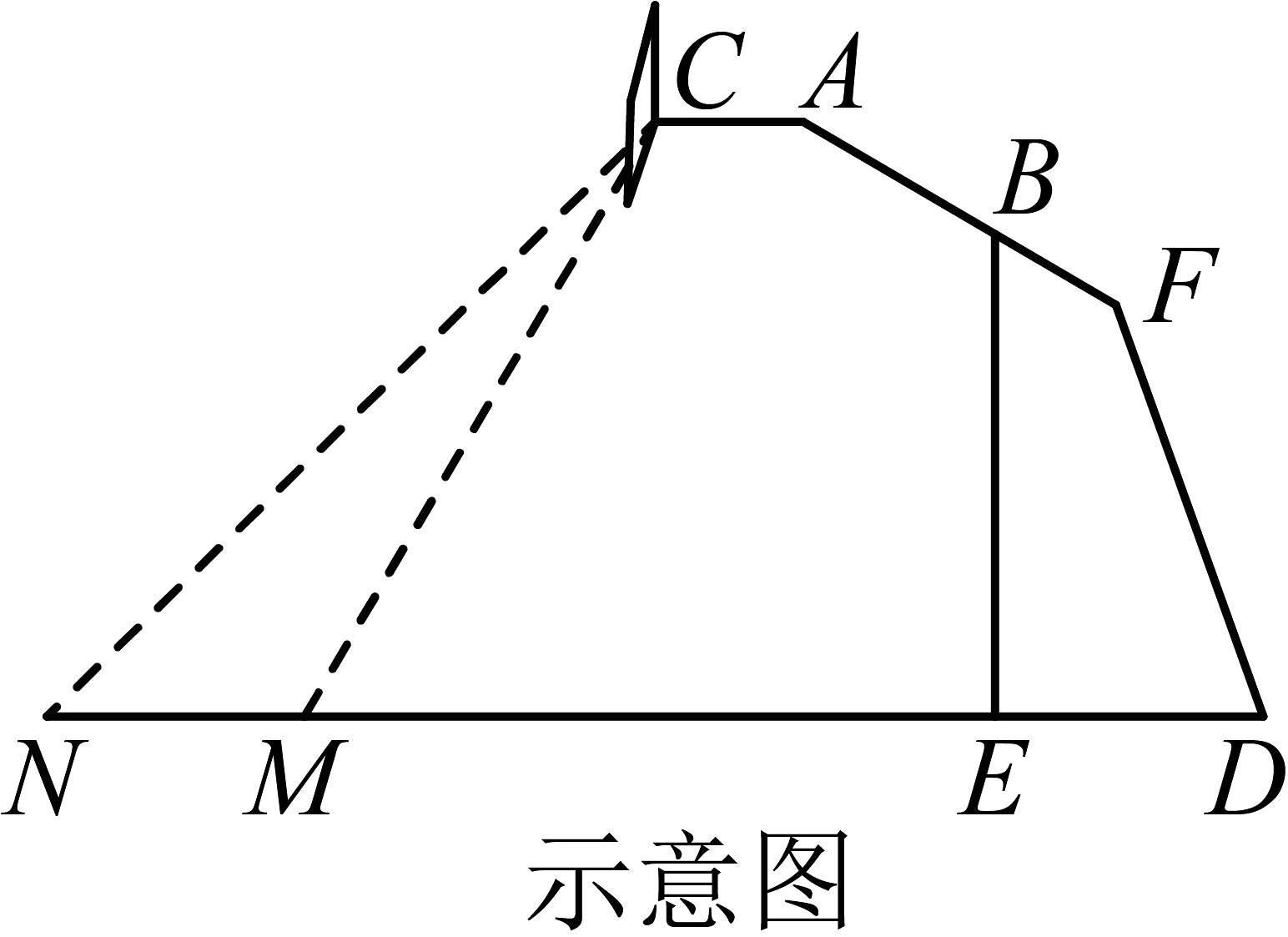
素材2
为计算篮球架的伸臂距离地面的高度,小明在点处测得:米,.在距离点左侧米的处测得: .
(参考数据: , , )
任务一
利用素材1,判断篮球架安装是否合格,并说明理由.(篮球架安装要求:伸臂地面 , 支架地面).
任务二
利用素材2,求篮球架的伸臂距离地面的高度.(结果保留一位小数)
-
19、如图,在中,点D为线段上任意一点.
 (1)、尺规作图:作线段的垂直平分线,分别交 , 于点E,F,连接 , ;(不写作法,保留作图痕迹)(2)、在(1)的基础上,线段与交于点G,已知________(请从“①平分;②点G为中点”这两个条件中选取一个作为已知条件).
(1)、尺规作图:作线段的垂直平分线,分别交 , 于点E,F,连接 , ;(不写作法,保留作图痕迹)(2)、在(1)的基础上,线段与交于点G,已知________(请从“①平分;②点G为中点”这两个条件中选取一个作为已知条件).求证:四边形是菱形.
-
20、某商店销售A、B两款2025年春晚“巳(sì)升升”吉祥物,销售B款吉祥物的单价比A款吉祥物的单价高20元,400元购买A款吉祥物数量和600元购买B款吉祥物的数量相同.(1)、求A、B两款吉祥物的销售单价;(2)、A款吉祥物的进价为25元/个,B款吉祥物的进价为48元/个.若该商店计划购进A、B两款吉祥物数量共60个,且B款吉祥物数量不低于A款吉祥物数量的2倍,则应如何进货能使得这批吉祥物全部售出后所获利润最大?最大利润是多少?