-
1、为了准备参加深圳市马拉松比赛,茗茗和清清约定每周六同时从A地到相距6000米的B地匀速往返跑(中途不休息),茗茗的速度大于清清的速度.图中的折线表示从开始到第二次相遇截止时,两人的距离y(米)与跑步时间x(分)之间的关系的图象,下列结论错误的是( )
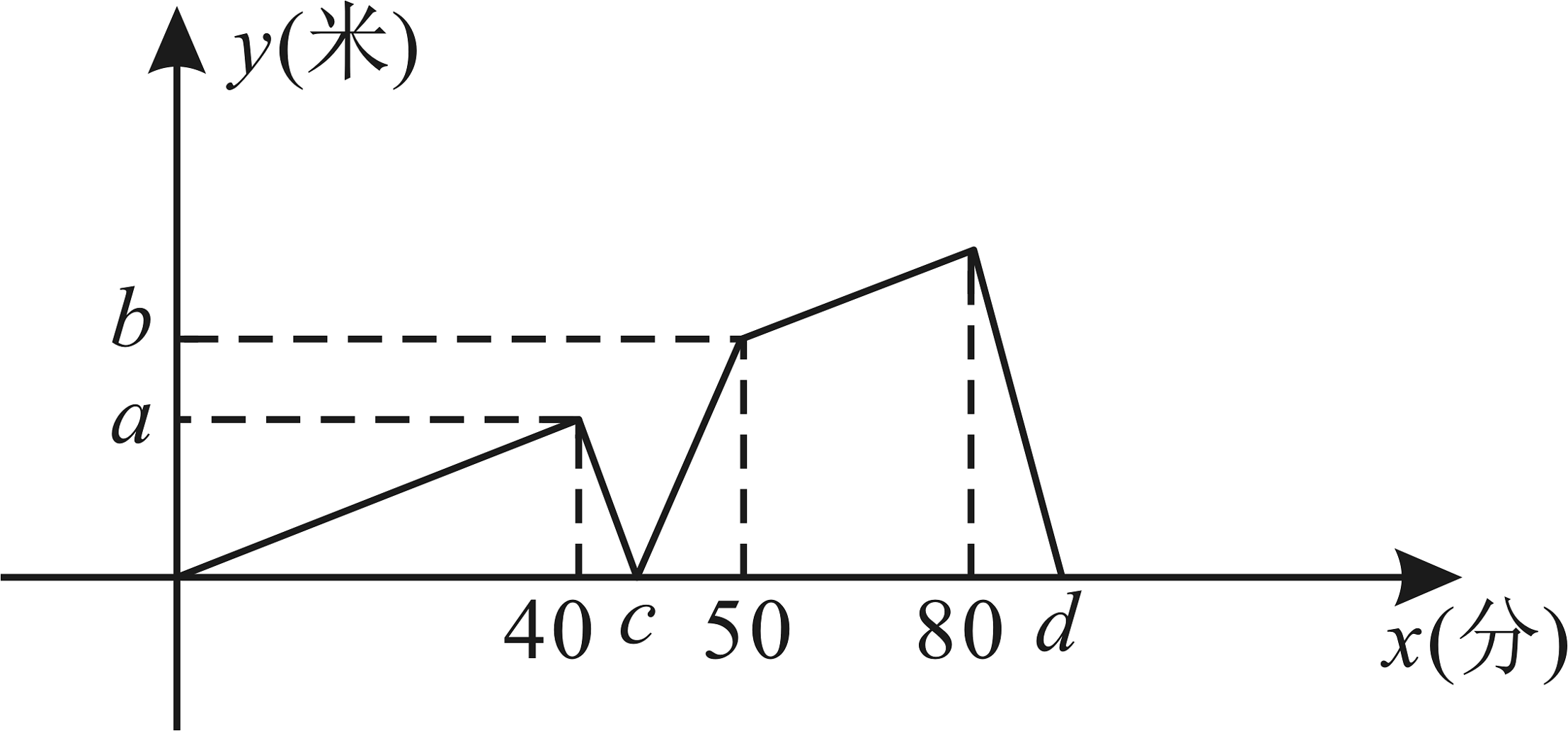 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,是外接圆,是的直径,连接 , , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、下列计算中,正确的是( )A、 B、 C、 D、
-
4、综合与实践【主题】足球最佳射门位置.

【素材】某足球场上,运动员在练习选择适合的位置射门.线段表示球门,、为射门张角.理论上当射门张度越大时,进球的可能性越大.如图1,_____.(用“”、“”或“”填空)
【实践探索】假设运动员沿着直线l带球跑动,寻找最佳射门位置.如图2,以线段为弦作 , 恰与直线相切,切点为A.若点M是上一个异于点A的动点,求证:当运动员跑动到切点A处时,射门张角最大,即 .
【迁移应用】如图3,点 , 点 , 点A为y轴正半轴上的一个动点,当最大时,请求出点A的坐标.
-
5、2025年央视春晚节目《秧BOT》以机器人表演传统秧歌为主题,燃爆全球,广受好评.为调查观众对某创新节目的评价,组委会收集了50名现场观众和5000名线上观众的评分(满分10分),并根据得分绘制了以下不完整的统计表和统计图:

两个观众群体对《秧BOT》打分样本数据的平均数、中位数、众数如下:
平均数
中位数
众数
现场
8
8
线上
7.6
7
(1)、直接写出 , , 的值;(2)、请你计算出线上观众评分不低于8分的总人数;(3)、小明认为线上观众群体对《秧BOT》打分样本数据更能贴合实际,你同意他的说法吗?简要说明理由. -
6、某户外实践活动小组欲测量球罐外斜梯的长度,实施了如下方案:先测得球罐最低处离地面高度米.接着一人站在球罐最高点处,看到斜梯末端处恰好被斜梯顶端遮挡(此时与⊙相切),已知过切点恰有一水平横梁交于斜梯末端处.
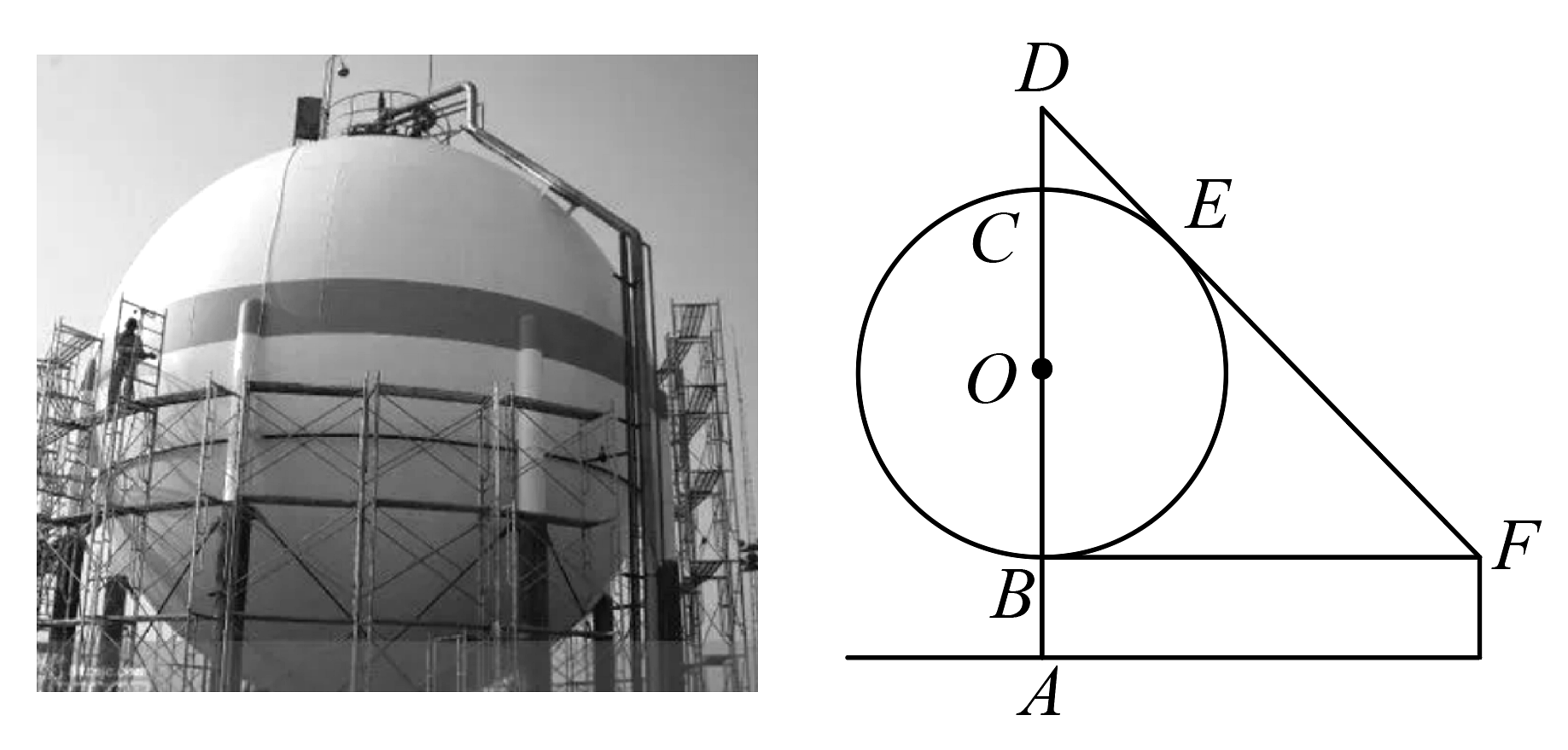 (1)、连接 , 求证:;(2)、若眼睛与点的距离为1.5米, , 求斜梯的长.
(1)、连接 , 求证:;(2)、若眼睛与点的距离为1.5米, , 求斜梯的长. -
7、如图,在中, , 分别是 , 的中点,连接 .
 (1)、实践与操作:作出线段的中点(尺规作图,保留痕迹,不写作法);(2)、应用与证明:在(1)的条件下,连接 , . 若 , , , 求证:四边形是菱形.
(1)、实践与操作:作出线段的中点(尺规作图,保留痕迹,不写作法);(2)、应用与证明:在(1)的条件下,连接 , . 若 , , , 求证:四边形是菱形. -
8、计算: .
-
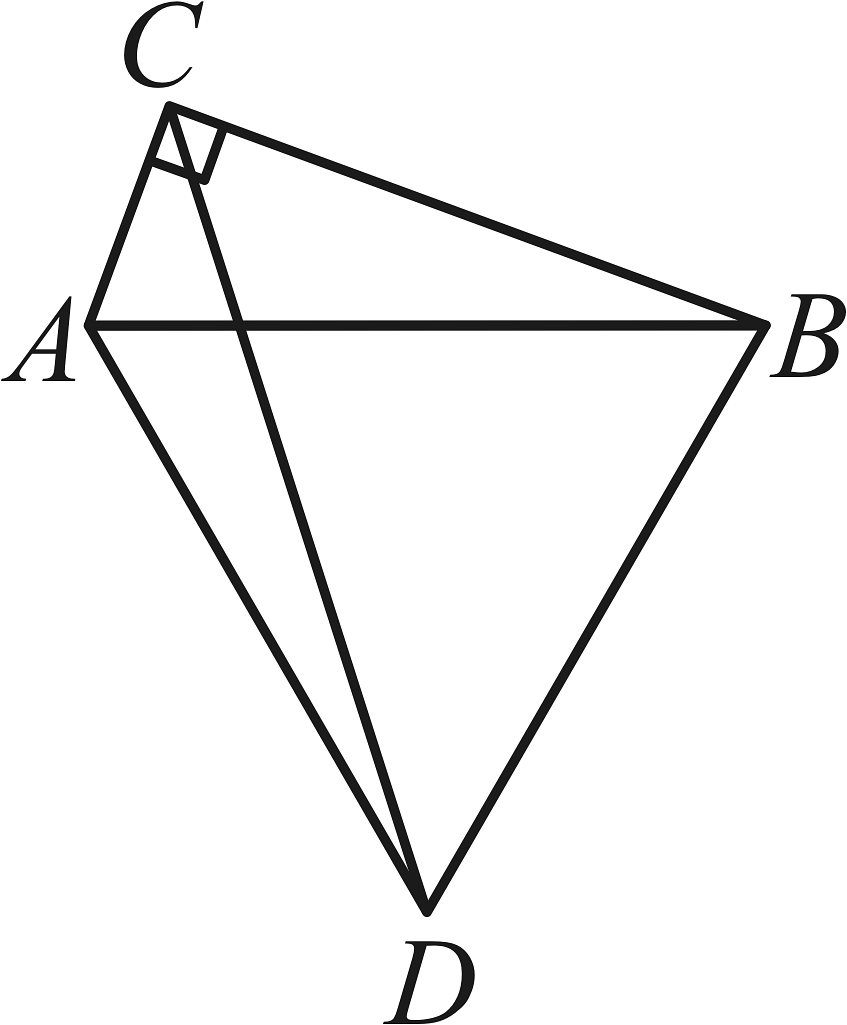
9、如图,在中, , , , 以为边向下作等边 , 则的长为 .
-
10、如图,函数和函数的图象相交于点 , , 若 , 则x的取值范围是( )
 A、 B、或 C、或 D、或
A、 B、或 C、或 D、或 -
11、如图,四边形为平行四边形, , , 相交于点 . 设和的面积分别为 , , 则( )
 A、1:2 B、1:3 C、4:9 D、1:4
A、1:2 B、1:3 C、4:9 D、1:4 -
12、科学家记录了四种花卉的平均开花天数(天数越短开花越快)和方差(方差越小开花越稳定),数据如表所示,开花最快且最稳定的是( )
种类
甲种类
乙种类
丙种类
丁种类
平均数
方差
A、甲种类 B、乙种类 C、丙种类 D、丁种类 -
13、随着时代到来,光纤通信越来越被大家熟知.如图,是光信号在光纤中传输的一小段过程,图示中可看作两个平行放置的平面镜,光信号经过平面镜反射时, , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( )
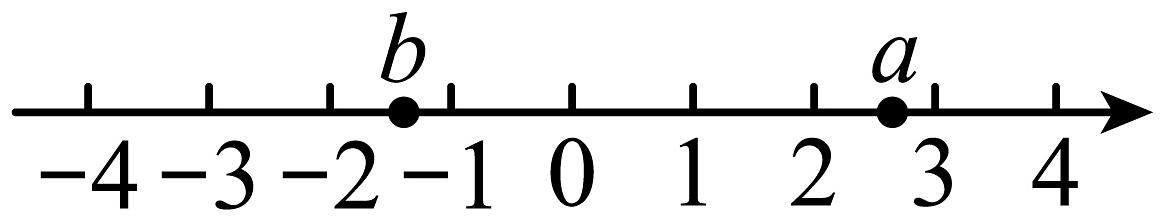 A、 B、 C、 D、
A、 B、 C、 D、 -
15、(深度求索)是由中国某公司开发的通用人工智能系统,以搜索增强架构和混合专家模型为核心技术,具备跨领域推理、实时信息处理与创造性输出能力.截至2025年3月,的全球日活跃用户总量达到亿,将数据亿用科学记数法表示是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、某市2025年1月份连续四天的天气预报信息如图所示,其中日温差最大的一天是( )
1月28日(除夕)
1月29日(春节)
1月30日(初二)
1月31日(初三)



 A、1月28日 B、1月29日 C、1月30日 D、1月31日
A、1月28日 B、1月29日 C、1月30日 D、1月31日 -
17、如图,在中, , . 点P从点A出发,沿向终点C运动,同时点Q从点C出发,沿运动,它们的速度均为每秒个单位长度,点P到达终点时,P,Q同时停止运动.当点P不与点A,C重合时,过点P作于点N,连接 , 以为邻边作 . 设与重叠部分图形的面积为S,点P的运动时间为t秒.
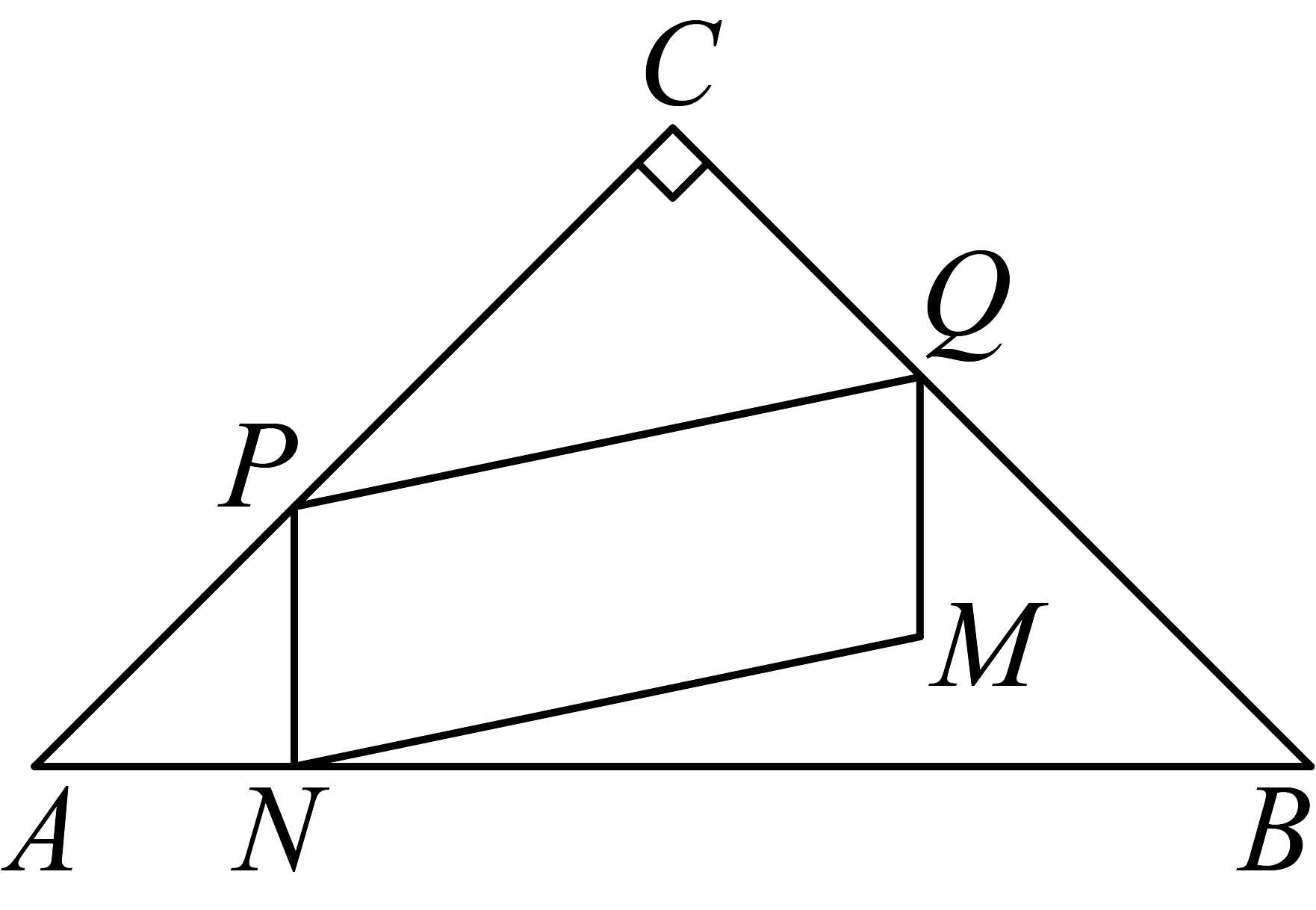 (1)、①的长为 ;
(1)、①的长为 ;②的长用含t的代数式表示为 .
(2)、用代数式表示S. -
18、如图,在平行四边形中,对角线和交于点O,点E、F分别为的中点,连接 .
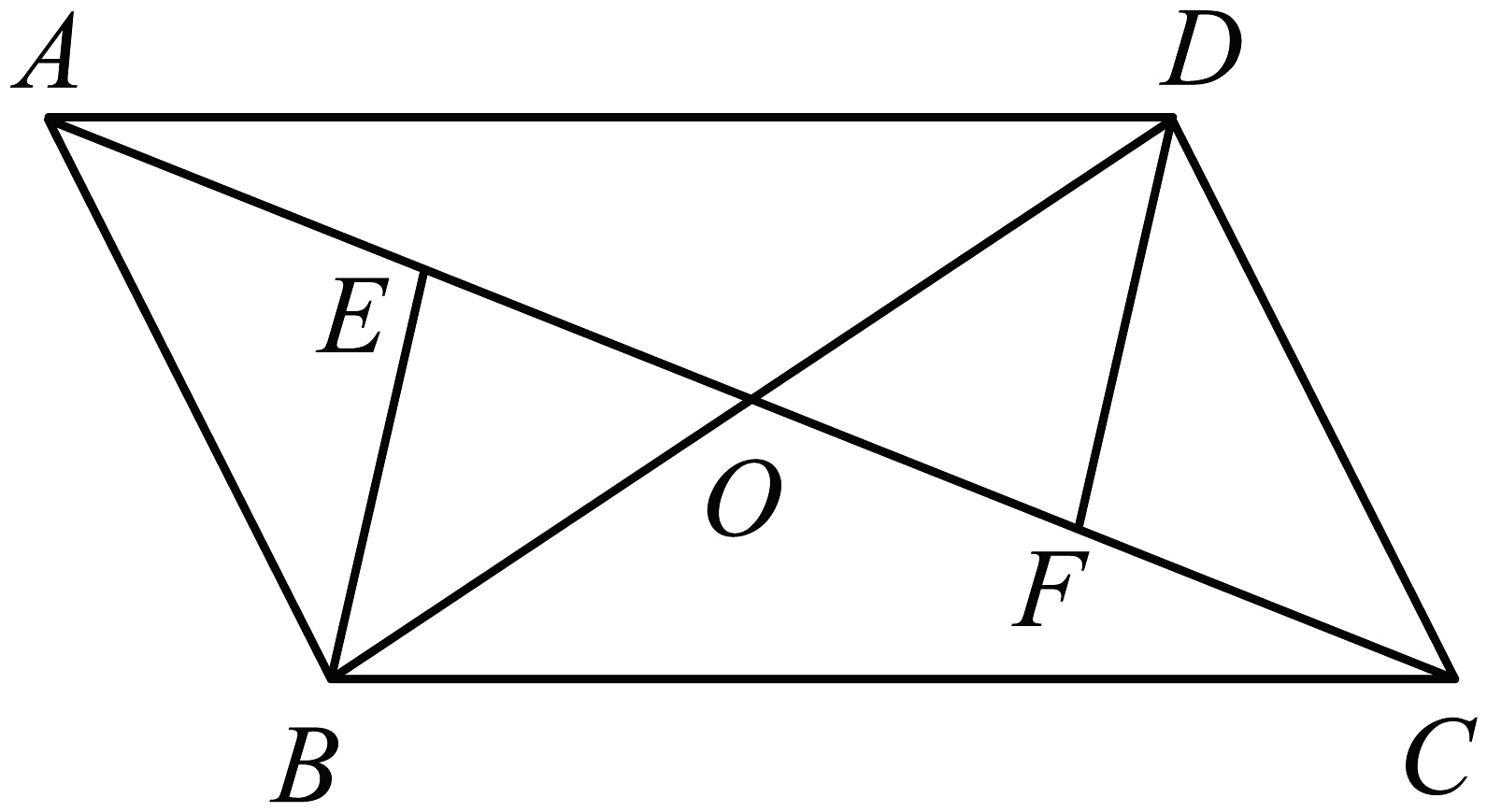 (1)、求证:;(2)、若 , 且 , 则的长为 .
(1)、求证:;(2)、若 , 且 , 则的长为 . -
19、如图,在四边形中, , 且 , 试求的度数.
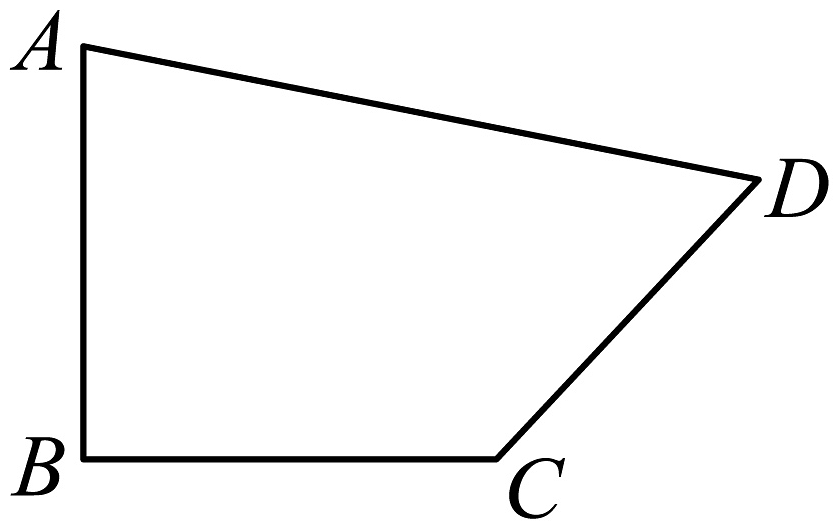
-
20、已知,的三边长分别为 , , , 且满足 .(1)、试判断的形状,并说明理由;(2)、若 , 求的面积.