-
1、如图,菱形中, , ;点是的中点,点是上一动点,连接 . 分别是的中点,连接 , 则的最小值是 .

-
2、在中,若 , , , 则的面积 .
-
3、如图,一个游泳爱好者,要横跨一条宽 的河流,由于水流速度的原因,这位游泳爱好者向下游偏离了 , 这位游泳爱好者在横跨河流时的实际游泳距离为米.

-
4、若 , 则的值为 .
-
5、如图,在正方形中,P为上一点(点P不与点B,C重合),于G,并交于点H,过C作交AH延长线于点F,则的值为( )
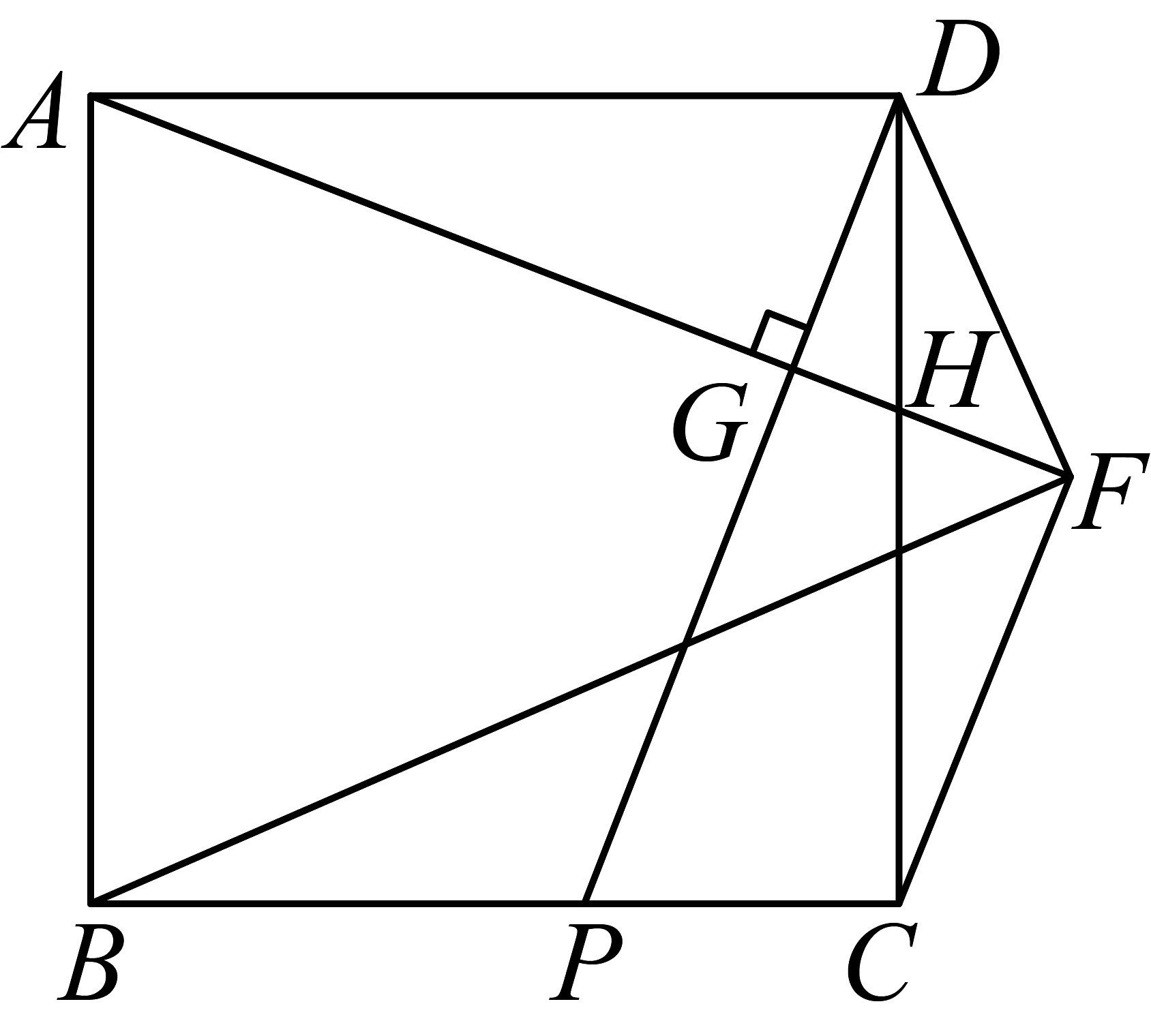 A、 B、 C、 D、
A、 B、 C、 D、 -
6、如图,在菱形中,若对角线 , 则菱形的周长为( )
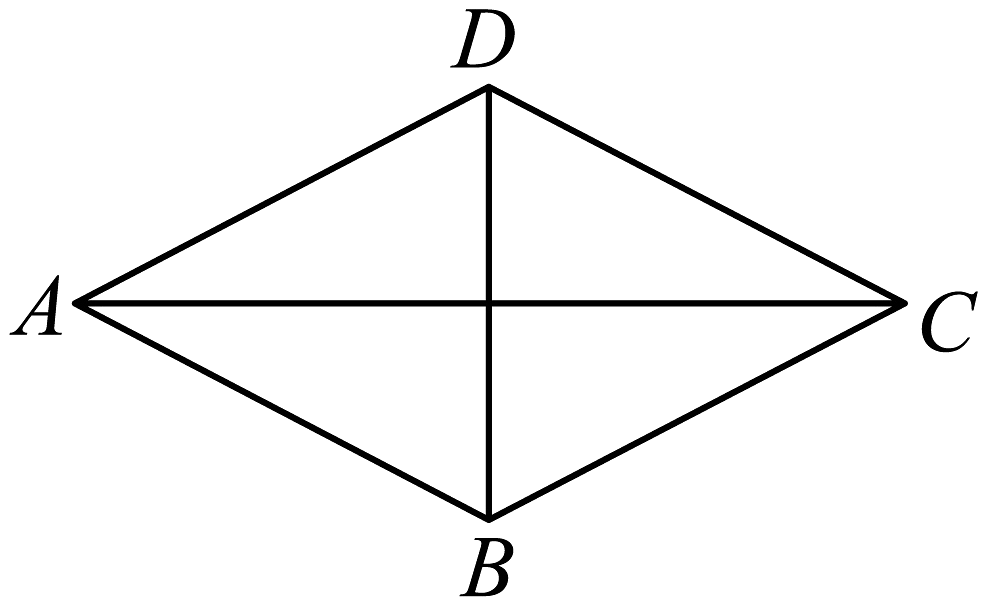 A、 B、 C、 D、
A、 B、 C、 D、 -
7、如图,矩形纸片, , 点P是边上一点, , 矩形纸片沿折叠,点A落在G处,的延长线交于点H,则的长为( )
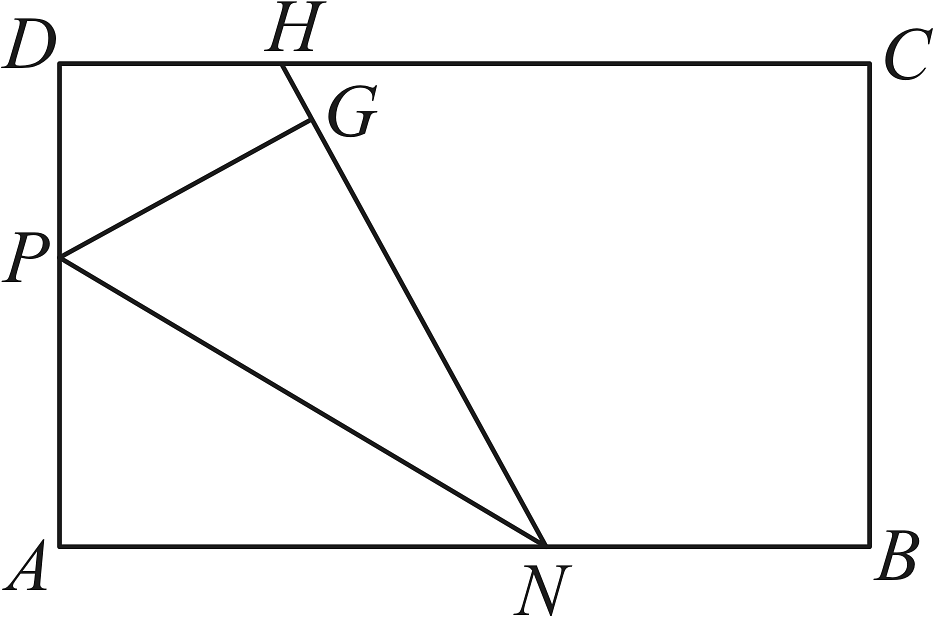 A、8 B、 C、10 D、
A、8 B、 C、10 D、 -
8、估计的值在( )A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间
-
9、如图所示,数轴上与点A所对应的实数为 , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、线段a,b,c组成的三角形,不是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,
-
11、下列运算正确的是( )A、 B、 C、 D、
-
12、综合与实践
【问题情境】小明在海边看到一艘装有四根大圆筒的轮船(如1图所示),通过查阅资料了解到这是马格努斯转子船,当圆筒高速旋转时,可以助推货轮前进,其原理是旋转的物体在流体(如空气或水)中运动时,会受到一个垂直于运动方向的力,这种物理现象被称为马格努斯效应(如2图所示).生活中的足球“香蕉球”、乒乓球弧圈球,都是马格努斯效应的常见例子.
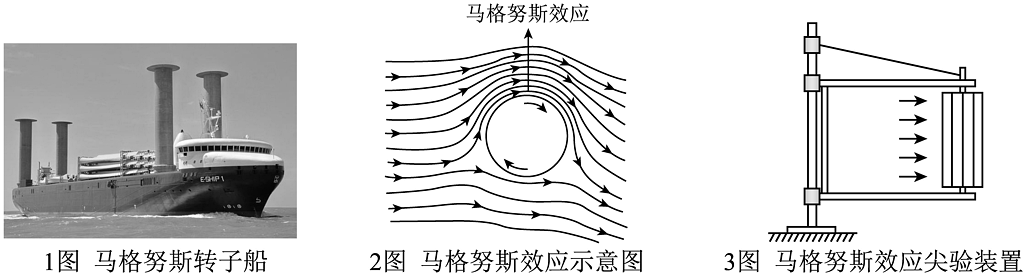
【设计方案】小明与同学组成科技小组,设计实验验证马格努斯效应.实验装置如3图所示,圆柱体模拟转子船的圆筒(圆柱体半径和高度都可以调节).已知装置产生的推力满足公式. , 其中k为比例系数(与圆柱体侧面积A有关,实验条件下关系近似为ω为电机控制圆柱体旋转的角速度(单位:),v为电风扇模拟的风速(单位:),产生的推力F可用测力计测量(单位:N).现有实验数据如下:
实验组
风速v()
旋转角速度ω()
推力F(N)
1
5
4
24
【问题解决】
(1)、保持风速不变,若要推力达到48N,求此时旋转角速度;(2)、保持风速不变,已知圆柱体的最高旋转角速度ω为10 .①现有装置能否产生100N的推力?请说明理由;
②已知初始时圆柱体半径 , 请设计一个改变圆柱体半径的方案(高度不变),使得装置在最高旋转角速度下能产生100N推力.(结果保留2位小数,计算过程中π取3)
-
13、在2025年1月28日晚央视春晚的舞台上,创意融合舞蹈《秧BOT》中机器人扭了秧歌舞、丢起了手绢,成为了全国观众的热议焦点.某科技公司为测试两款人形机器人(甲型和乙型),给这两款机器人制定了以下任务:(1)、搬运重物、以下记录了它们在相同环境下各完成5次搬运任务的时间(单位:秒):
甲型机器人:38,39,41,43,39
乙型机器人:50,48,32,33,34
请通过计算,从完成搬运任务时间的平均数及极差比较这两款机器人.
(2)、家政服务.以下是专业评委根据相关标准对两款机器人在4个方面的表现给出的评分(满分10分,得分越高则表现越好)功能性
交互性
安全性
采购价格
甲型机器人
10
8
9
8
乙型机器人
8
8
8
10
如果你是某养老院的采购人员,请制定适当的标准采购最合适的家政服务机器人,并说明理由.(要求兼顾功能性、交互性、安全性及采购价格)
-
14、如图,点E为平行四边形对角线BD上一点.
 (1)、用尺规作图法作点F为线段BD上的点.(保留作图痕迹,不要求写作法)(2)、连接CE,若经过A、C、E三点的圆也经过点F,求证:
(1)、用尺规作图法作点F为线段BD上的点.(保留作图痕迹,不要求写作法)(2)、连接CE,若经过A、C、E三点的圆也经过点F,求证: -
15、广州起义烈士纪念碑位于广州市,它由底部雕塑和顶部雕塑组成,顶部雕塑的造型是手臂紧握系着标志起义的红布带的汉阳造步枪.同学们来到广州起义烈士陵园,了解广州起义的相关历史背景并用无人机收集到以下数据:如图,点A是纪念碑顶部一点,的长表示顶部雕塑的高度,点E为点A正上方一点,(米,米.请根据上述数据,计算广州起义烈士纪念碑的高度(结果精确到1米).
参考数据: .

-
16、先化简,再求值: , 其中 .
-
17、如图,菱形的周长为24, , 以点B为圆心的与分别相切,则图中阴影部分(即扇形)的面积是(结果保留π)
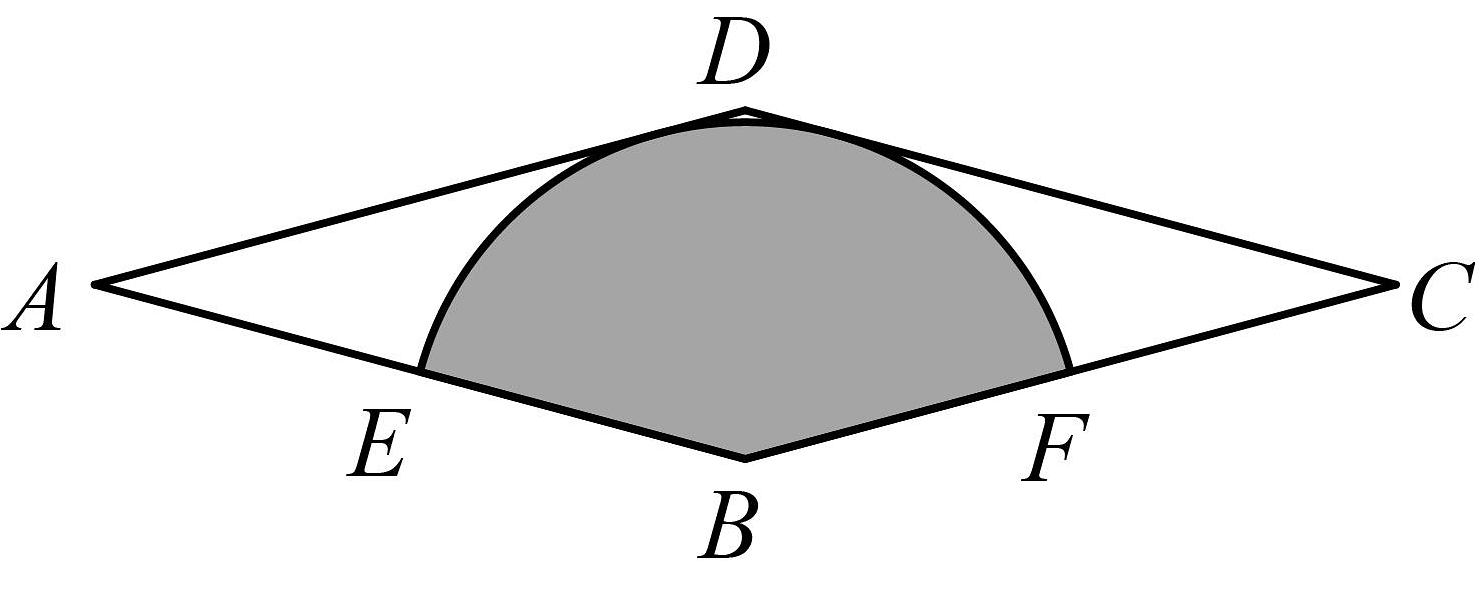
-
18、2025年4月,我国跳水名将陈芋汐在跳水世界杯夺得金牌,其中一跳的有效得分分别为10,8,8,9,9,则这组数据的中位数是
-
19、分解因式:
-
20、下列不等式中,与不等式组成的不等式组只有一个整数解的是( )A、 B、 C、 D、