相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图,在中, , , , 点Q在边上, , 点P在边上, , 垂足为H.
 (1)、求证: .(2)、求的长.
(1)、求证: .(2)、求的长. -
2、如图,已知反比例函数的图象与直线相交于 , B两点.
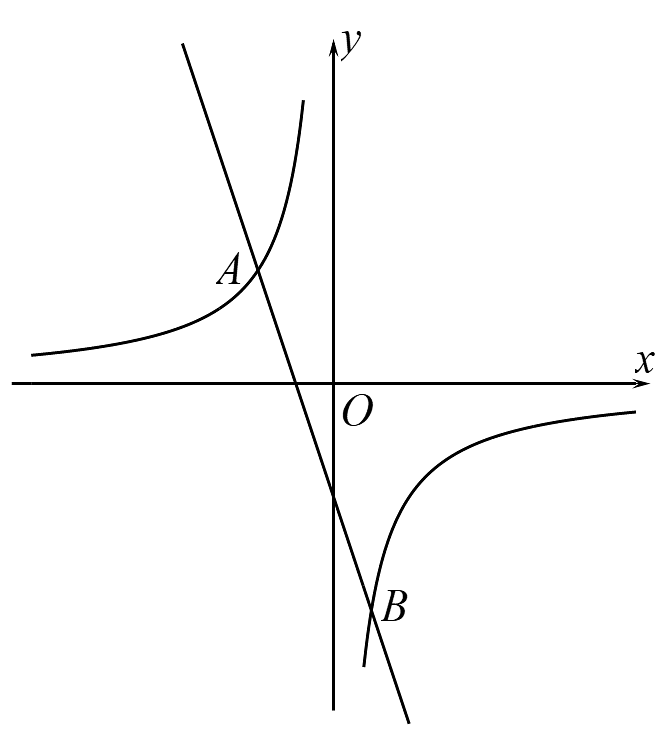 (1)、求k的值.(2)、当时,请直接写出x的取值范围.
(1)、求k的值.(2)、当时,请直接写出x的取值范围. -
3、定义:在平面直角坐标系中,横、纵坐标相等的点为“完美点”,顶点是“完美点”的二次函数为“完美函数”.(1)、若点是“完美点”,求a的值.(2)、已知某“完美函数”的顶点在直线上,且与y轴的交点到原点的距离为4,求该“完美函数”的解析式.
-
4、杠杆原理也称为“杠杆平衡条件”,要使杠杆平衡,作用在杠杆上两个力矩(力与力臂的乘积)大小必须相等,即:阻力阻力臂动力动力臂,用代数式表示为 . 如图,已知石头重量(阻力)为 , 阻力臂长 , 小华想用一根撬棍撬起这块石头,但他只有的力量,那么他该选择动力臂为多少米的撬棍才能撬动这块大石头?

-
5、如图,在边长为1个单位长度的小正方形组成的网格中,建立平面直角坐标系 , 的三个顶点A,B,C都在格点(网格线的交点)上.
 (1)、将向左平移6个单位长度,得到 , 画出 .(2)、画出与相似的 , 使它与的相似比为 .
(1)、将向左平移6个单位长度,得到 , 画出 .(2)、画出与相似的 , 使它与的相似比为 . -
6、如图, , 直线m,n分别与直线a,b,c交于点B,C,E和点A,D,F.已知 , , , 求线段的长.

-
7、如图,点C的坐标为 , 是x轴上的一动点,B为y轴上一点,且 , .

(1)如图1,当时, .
(2)如图2,连接 , F为的中点,在点A从原点O运动到点的过程中,点F所经过的路线长是 .
-
8、如图,在平面直角坐标系中,直线与坐标轴交于A,B两点,且与反比例函数的图象交于点C,D,则的面积为 .

-
9、如图,某小区地下车库入口栏杆短臂 , 长臂 , 当短臂端点A下降时,长臂端点B升高 m.

-
10、在同一平面直角坐标系中,若 , 则函数与的大致图象是( )A、
 B、
B、 C、
C、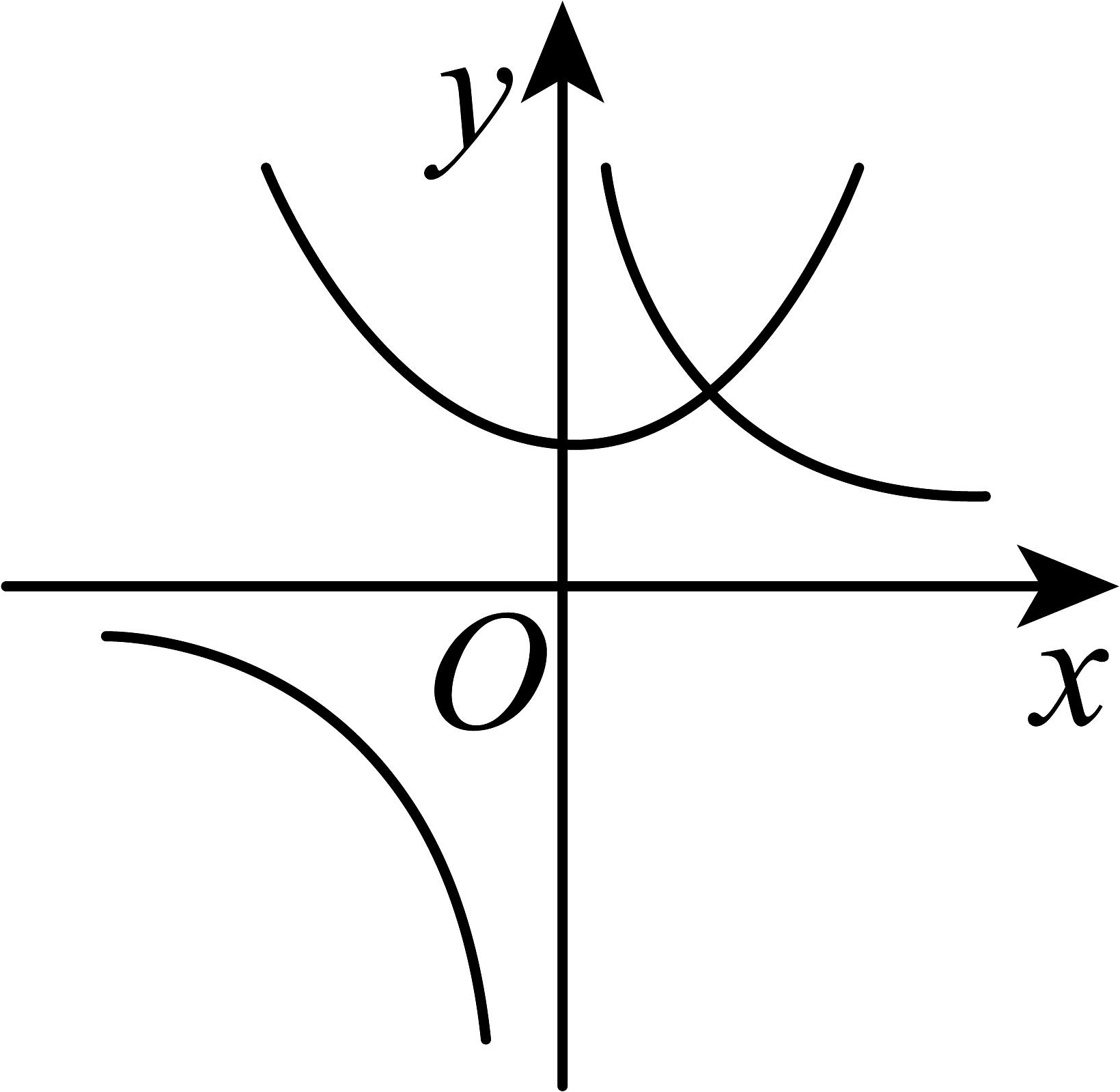 D、
D、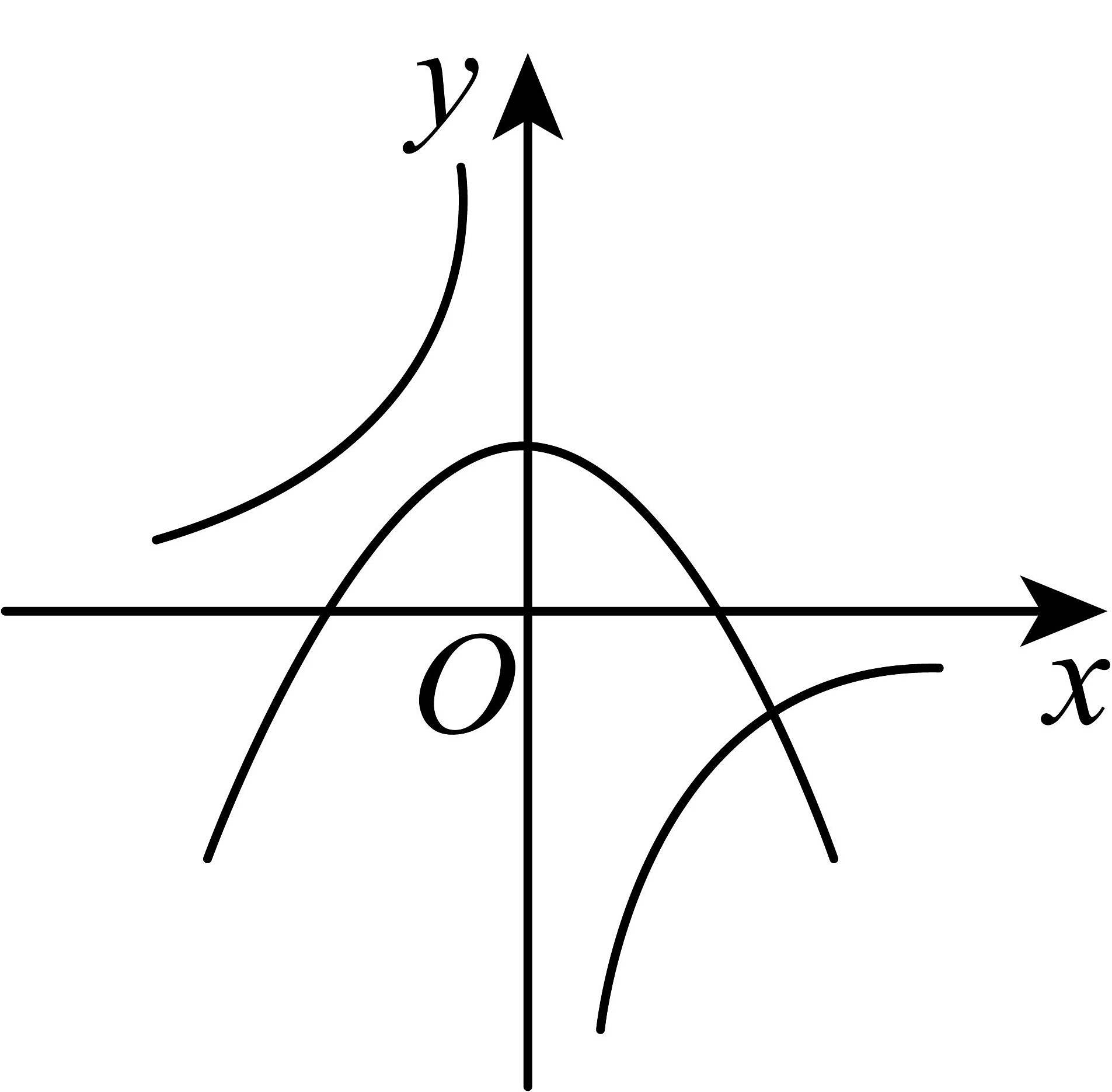
-
11、如图,这是某平台销售的折叠椅子的示意图,与地面平行,已知 , , 若 , 则的长是( )
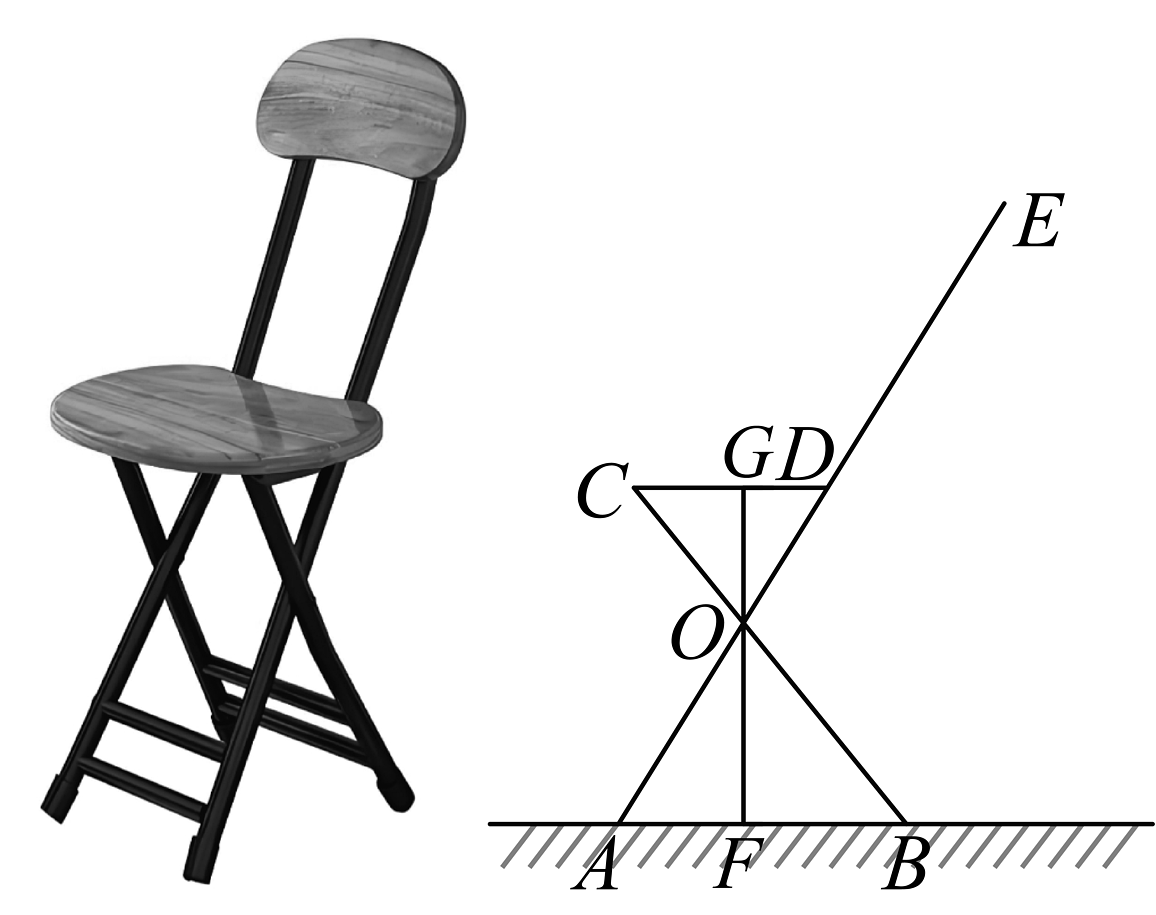 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图,抛物线与轴交于 , , 则关于的方程的解为( )
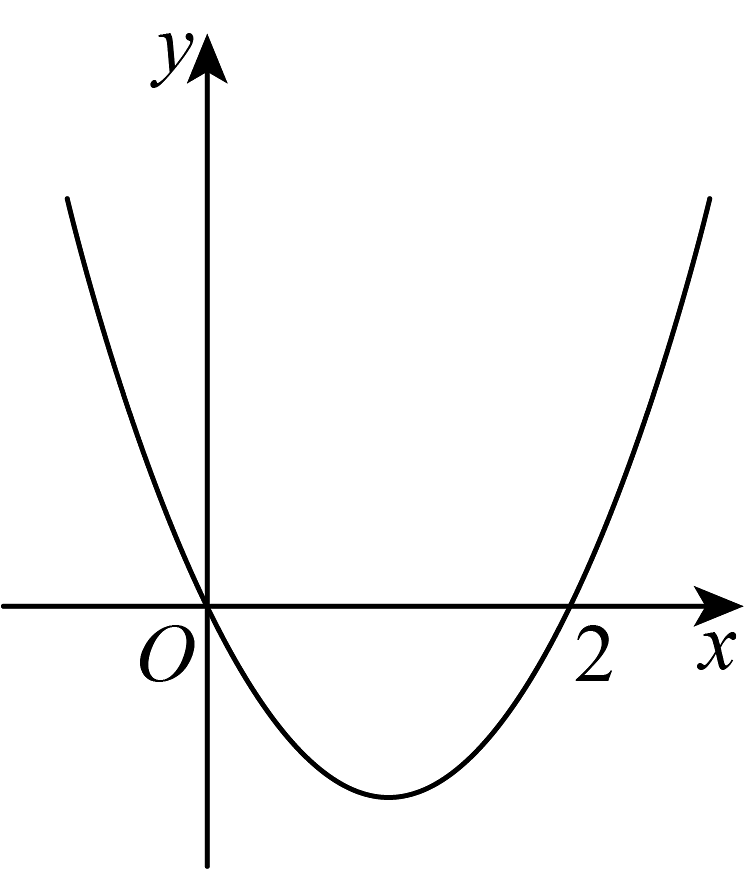 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
13、如图,的顶点分别在坐标轴和反比例函数的图象上,并且的面积为6,则k的值为( )
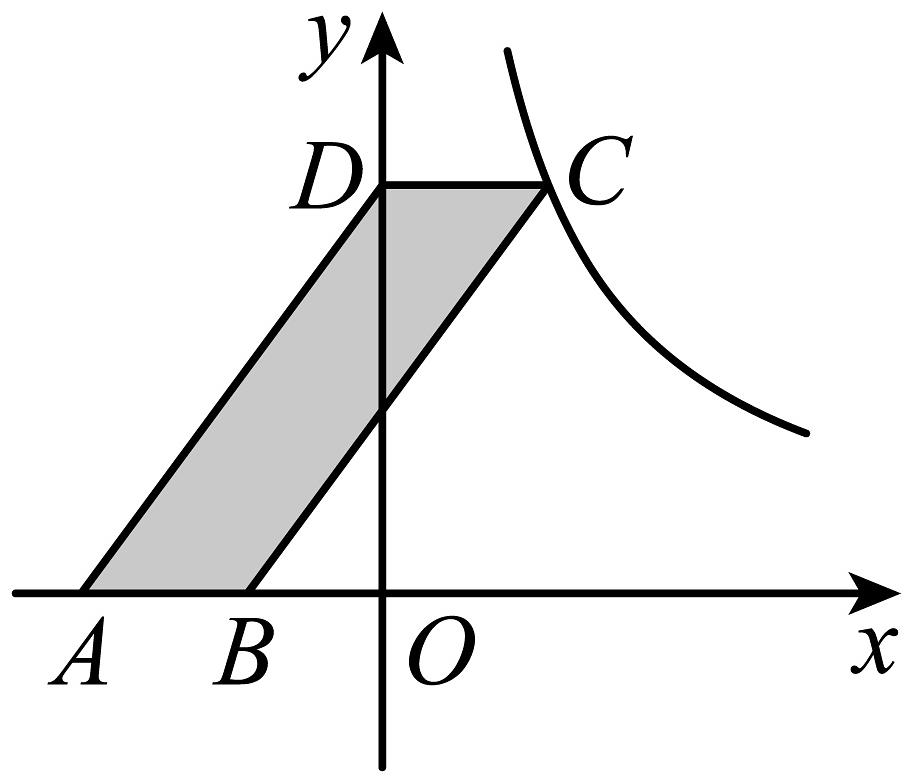 A、6 B、 C、3 D、
A、6 B、 C、3 D、 -
14、如图,在中,D是上一点,连接 , 下列条件中不能判断的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、将抛物线先向右平移2个单位长度,再向下平移1个单位长度,平移后对应的二次函数解析式为( )A、 B、 C、 D、
-
16、下列各组图中,是相似图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
17、下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、
-
18、如图,已知直线y=x﹣4分别与x轴,y轴交于A,B两点,直线OG:y=kx(k<0)交AB于点D.
(1)求A,B两点的坐标;
(2)如图1,点E是线段OB的中点,连接AE,点F是射线OG上一点,当OG⊥AE,且OF=AE时,求EF的长;
(3)如图2,若k= , 过B点BCOG,交x轴于点C,此时在x轴上是否存在点M,使∠ABM+∠CBO=45°,若存在,求出点M的坐标;若不存在,请说明理由.

-
19、勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
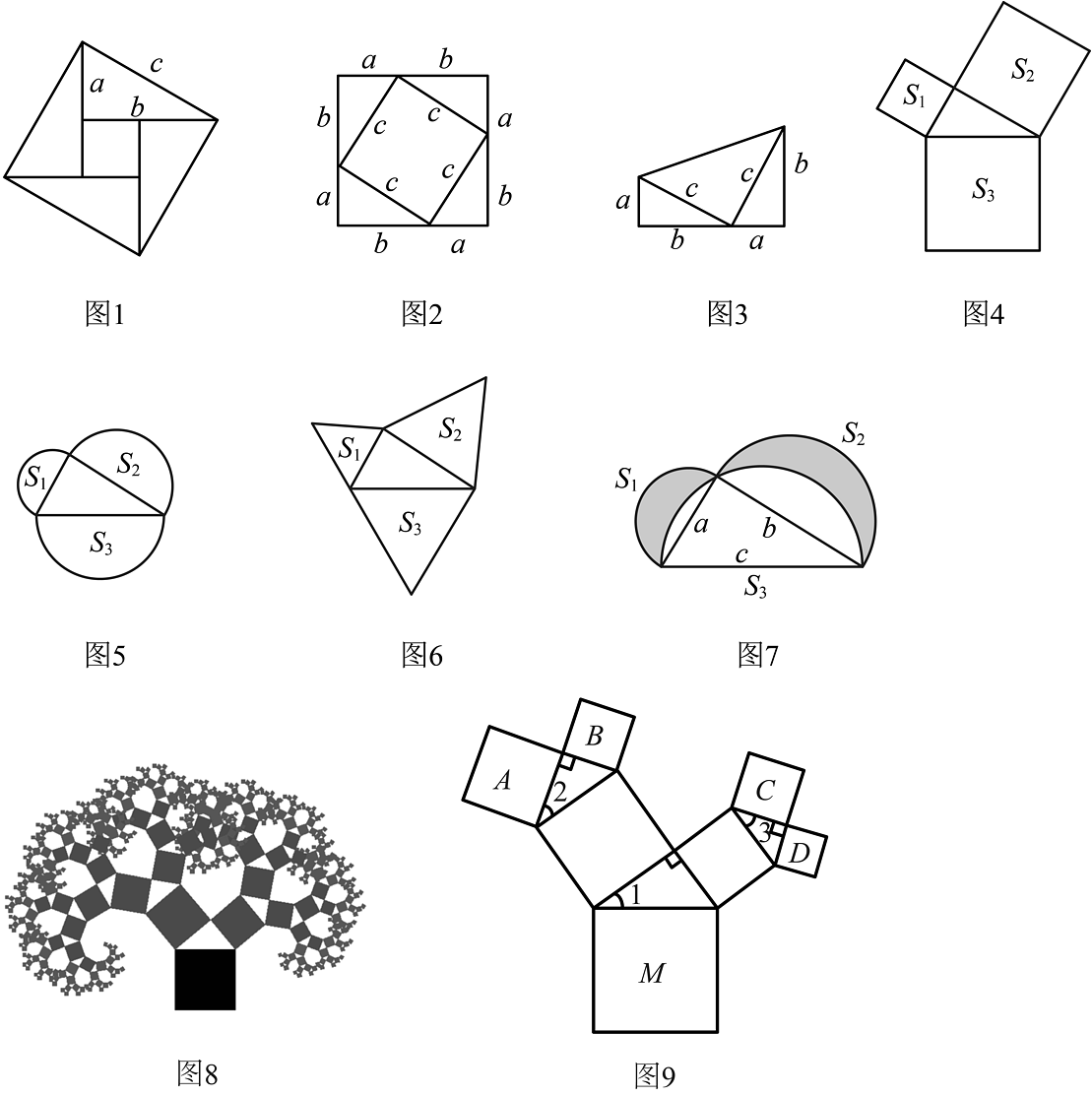 (1)、①如果用a,b和c分别表示直角三角形的两直角边和斜边,则______(用含有a,b和c的式子表示三者之间的等量关系);
(1)、①如果用a,b和c分别表示直角三角形的两直角边和斜边,则______(用含有a,b和c的式子表示三者之间的等量关系);②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)、①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足的有______个;②如图7所示,分别以直角三角形两直角边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 , , 直角三角形面积为 , 请判断 , , 的关系并证明;
(3)、如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知 , 则当变化时,回答下列问题:(结果可用含m的式子表示)则:①______.
②b与c的关系为______,a与d的关系为______.
-
20、周末,小丽和爸爸、妈妈一家三口去杨梅园游玩.已知该杨梅园内的杨梅单价是每千克40元.为满足客户需求,该杨梅园现推出两种不同的销售方案:
甲方案:游客进园需购买30元的门票,采摘的杨梅按原价的六折收费;
乙方案:游客进园不需购买门票,采摘的杨梅在10千克以内按原价收费、超过10千克后,10千克部分按原价收费,超过部分按原价的五折收费.
设采摘量为x千克,按甲方案所需总费用为元,按乙方案所需总费用为元.
(1)、当采摘量超过10千克时,分别求出、关于x的函数表达式;(2)、若采摘量为30千克,选择哪种方案更划算?请说明理由.