相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图,抛物线 与x轴交于A,B 两点(点A 在点 B 左侧),与y轴交于点 C,P 是直线 BC 上一动点,Q是x轴上一动点,连接AP,PQ,则AP+PQ的最小值为.

-
2、如图,在等腰三角形ABC中,点 D 为AC的中点,M,N分别是AB,BC 上的动点,若CD=2,∠A=120°,则 DN+MN 的最小值为.

-
3、 如图,在△ABC 中,AB =4,∠BAC = 45°,∠BAC 的平分线交 BC 于点 D,E,F 分别是边AD,AB 上的动点,则 BE+EF 的最小值是.

-
4、 如图,正方形 ABCD 的对角线 AC,BD 相交于点O,点P 为 BC 边上一动点(不与点 B,C重合),PE⊥OB 于点 E,PF⊥OC 于点 F.若AB=20,则EF的最小值为 ( )
 A、10 B、 C、20 D、
A、10 B、 C、20 D、 -
5、如图,四边形ABCD是菱形,∠A=60°,延长AD 到点E,使DE=AD,连接BD,BE,CE.点P是BC的中点,M,N分别在线段CE,BE上.若AB=6,则PN+NM 的最小值为.

-
6、如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,点E是AB上任意一点,若AD=5,AC=4,则 DE 的最小值为 ( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
7、如图,抛物线 与x轴交于点A(4,0),与y轴交于点B(0,6).
 (1)、求抛物线的解析式;(2)、在x轴上有一动点 P(m,0)(点 P不与点A,点O 重合),过点 P作x轴的垂线交直线AB 于点 N,交抛物线于点 M.若 PN:MN=1:3,求m的值.
(1)、求抛物线的解析式;(2)、在x轴上有一动点 P(m,0)(点 P不与点A,点O 重合),过点 P作x轴的垂线交直线AB 于点 N,交抛物线于点 M.若 PN:MN=1:3,求m的值. -
8、如图,E是菱形ABCD对角线AC上的一点,连接BE,DE,CE=DE.
 (1)、求证:∠DEB=2∠DAB;(2)、求证:
(1)、求证:∠DEB=2∠DAB;(2)、求证: -
9、如图,在矩形 ABCD 中,点E 是 AB 的中点,点F 是 BC 上的一点,AB=8,∠FED=30°,∠FDE=45°,则 BC 的长度为.

-
10、 如图,在△ABC中,过点A 作AD⊥BC 于点D,正方形EFGH内接于△ABC,点H,G在边BC上,点 E,F分别在边AB 和AC 上.若AD=5cm,BC=10 cm,则正方形 EFGH的边长为 cm.

-
11、 如图,在⊙O 中,AB 是⊙O 的直径,CD 是⊙O 的切线,若 则⊙O的半径为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图,在四边形ABCD中,点 E 是BC的中点,连接AC,DE,交于点 F,且∠AFD=∠B.若CE=2,AC=5,则下列结论正确的是( )
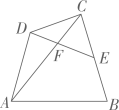 A、AB:EF=5:3 B、 C、 D、△CEF∽△CAB
A、AB:EF=5:3 B、 C、 D、△CEF∽△CAB -
13、 如图,在△ABC中,点 D,E分别在边AB,AC上,连接DE,且DE∥BC,若AD=3,AB=4,S四边形DECB=14,则S△ABC= ( )
 A、50 B、40 C、32 D、26
A、50 B、40 C、32 D、26 -
14、如图,在Rt△ABC中, 点D是AB边上的点, 交AC于点E, AB=10,则BC的长为.

-
15、如图,在▱ABCD中,点E 在边AD上,连接BE并延长交CD的延长线于点F,若AE=2ED,DE∥BC则FD:FC的值为.
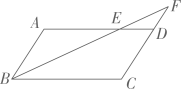
-
16、已知 , 互为倒数, , 互为相反数, , 求的值.
-
17、先化简,再求值: . 其中 , .
-
18、计算:(1)、(2)、(3)、(4)、
-
19、如图所示的日历中,带阴影的方框里有四个数,随着方框的移动,方框里的四个数存在一定的关系.设方框里最小的一个数为 , 则这四个数之和为(用含的代数式表示,并化为最简).

-
20、计算的结果是 .