相关试卷

1、计算 ${(- 1)}^{2014} + {(- 1)}^{2025}$ 的结果是（）

A、0 B、 $- 1$ C、 $- 2$ D、2

查看解析
2、我国古代数学家祖冲之算出的圆周率的近似值在3.1415926和3.1415927之间，并提出圆周率的约率为 $\frac{22}{7}$ ，密率为 $\frac{355}{113}$ ．下列对圆周率取近似数错误的是（）

A、3.1（精确到十分位） B、3.14（精确到0.01） C、3.141（精确到千分位） D、3.1416（精确到0.0001）

查看解析
3、2024年10月17日，习近平总书记在安徽省合肥市考察了合肥滨湖科学城，了解当地推进科技体制创新、加快科技成果转化等情况.据报道，自运营以来，滨湖科学城大力推进安徽科技大市场建设，累计挖掘国内外成果1.8万项，挂牌、转化科技成果3027项，含成立公司160家，促成科技成果转化交易金额超1173亿元，其中1173亿用科学记数法表示为（）

A、 $0.1173 \times 10^{12}$ B、 $1.173 \times 10^{12}$ C、 $1.173 \times 10^{11}$ D、 $11.73 \times 10^{10}$

查看解析
4、 $- 2024$ 的相反数为（）．

A、 $- 2024$ B、2024 C、 $- \frac{1}{2024}$ D、 $\frac{1}{2024}$

查看解析
5、要使一个六边形框架稳固且不活动，至少要钉根木条．

查看解析
6、如图，已知二次函数 $y = a x^{2} + 2 x + c$ 的图象与x轴交于A，B两点．A点坐标为 $(- 1, 0)$ ，与y轴交于点 $C (0, 3)$ ，点M为抛物线顶点，点E为AB中点．
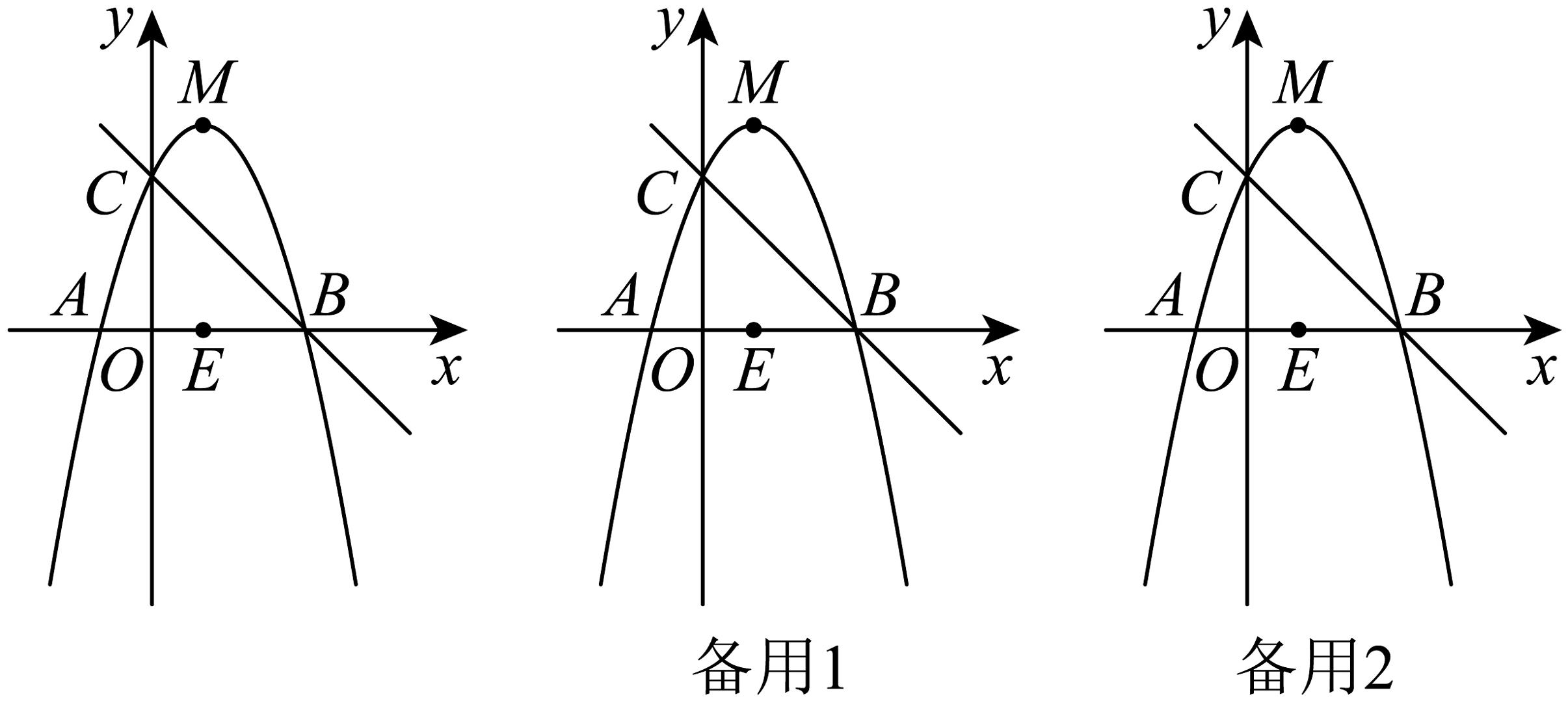AI

(1)、求二次函数的表达式；

(2)、在直线BC上方的抛物线上存在点Q，使得 $∠ Q C B = 2 ∠ A B C$ ，求点Q的坐标；

(3)、已知D，F为抛物线上不与A，B重合的相异两点，若直线AD，BF交于点P，则无论D，F在抛物线上如何运动，当D，E，F三点共线时，试判断 $△ A B P$ 的面积是否为定值，若是，请求出定值：若不是，请说明理由．

查看解析
7、【课本再现】
例1 在同一直角坐标系中，画出函数 $y = \frac{1}{2} x^{2}$ ， $y = 2 x^{2}$ 的图象．
例2 分别列表，再画出它们的图象（图1）．
$x$
$\cdot \cdot \cdot$
$- 4$
$- 3$
$- 2$
$- 1$
0
1
2
3
4
$\cdot \cdot \cdot$
$y = \frac{1}{2} x^{2}$
$\cdot \cdot \cdot$
8
4.5
2
0.5
0
0.5
2
4.5
8
$\cdot \cdot \cdot$
$x$
$\cdot \cdot \cdot$
$- 2$
$- 1.5$
$- 1$
$- 0.5$
0
0.5
1
1.5
2
$\cdot \cdot \cdot$
$y = 2 x^{2}$
$\cdot \cdot \cdot$
8
4.5
2
0.5
0
0.5
2
4.5
8
$\cdot \cdot \cdot$
（1）如图2是二次函数 $y_{1} = 2 x^{2}$ 的图像，在图中画出一次函数 $y_{2} = 2 x + 4$ 的图像，并求出二次函数 $y_{1} = 2 x^{2}$ 与一次函数 $y_{2} = 2 x + 4$ 的交点；
（2）利用图像直接写出当 $y_{1} \leq y_{2}$ 时，自变量的取值范围．
【拓展应用】
秦明同学在解题中发现，两个函数的交点情况与一元二次方程的解的情况有密切的联系．既而深入思考“将一次函数 $y_{2} = 2 x + 4$ 的图像向下平移多少个单位长度能与二次函数 $y_{1} = 2 x^{2}$ 的图像有且只有一个交点”，请你帮他解决这个问题．

查看解析
8、四边形 $A B C D$ 是正方形，E、F分别是 $D C$ 和 $C B$ 的延长线上的点，且 $D E = B F$ ，连接 $A E 、 A F 、 E F$ ．

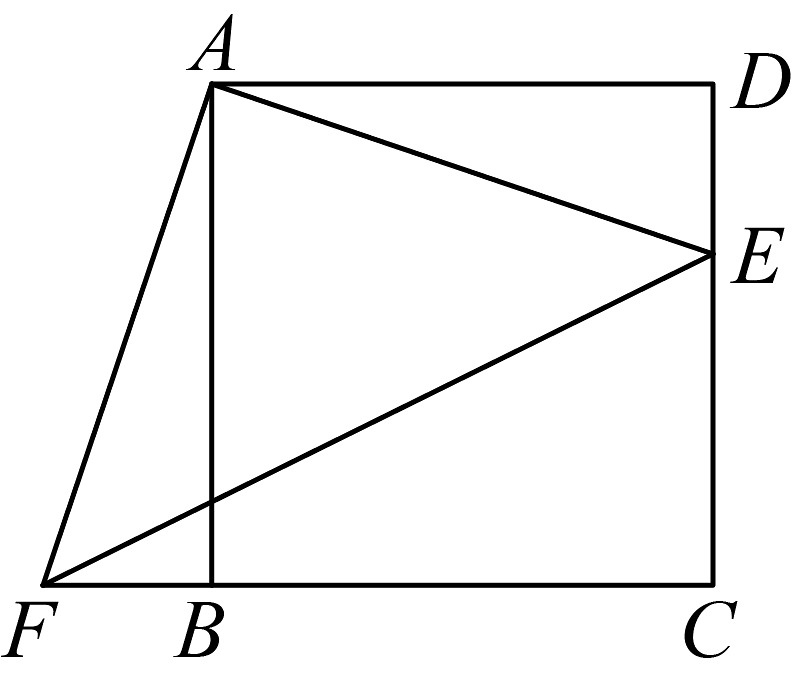(1)、试判断 $△ A E F$ 的形状，并说明理由；

(2)、填空： $△ A B F$ 可以由 $△ A D E$ 绕旋转中心点，按顺时针方向旋转度得到；

(3)、若 $B C = 8$ ，则四边形 $A E C F$ 的面积为．（直接写结果）

查看解析
9、如图，在平面直角坐标系中，将边长为 $a$ 的正方形 $O A B C$ 绕点 $O$ 顺时针旋转 $45^{°}$ 后得到正方形 $O A_{1} B_{1} C_{1}$ ．依此方式连续旋转 $2024$ 次得到正方形 $O A_{2024} B_{2024} C_{2024}$ ，那么点 $A_{2024}$ 的坐标是（）

A、 $(a, 0)$ B、 $(\frac{\sqrt{2}}{2} a, - \frac{\sqrt{2}}{2} a)$ C、 $(- \frac{\sqrt{2}}{2} a, - \frac{\sqrt{2}}{2} a)$ D、 $(0, a)$

查看解析
10、如图，Rt $△$ ABC中，∠A＝90°，∠ABC＝40°，将Rt $△$ ABC绕着点C逆时针旋转得Rt $△$ EDC，且点E正好落在BC上，连接BD，则∠CBD的度数为（　　）

A、40° B、55° C、60° D、65°

查看解析
11、如图， $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 关于点 $O$ 成中心对称，下列说法：
① $∠ B A C = ∠ B_{1} A_{1} C_{1}$ ；② $A C = A_{1} C_{1}$ ；③ $O A = O A_{1}$ ；④ $△ A B C$ 与 $△ A_{1} B_{1} C_{1}$ 的面积相等，其中正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看解析
12、问题背景及探索：
（1）已知在 $△ A B C$ 中， $A B = A C$ ， E、D都在边 $B C$ 上，
①如图1，若将 $△ A D C$ 绕点A顺时针旋转，当 $A C$ 与 $A B$ 重合时，点D旋转到 $D^{'}$ ，且 $D^{'} E = D E$ ，求出 $∠ E A D$ ， $∠ B A E$ ， $∠ C A D$ 数量关系；
②如图2，若 $A B ⊥ A C$ ， $E D^{2} = B E^{2} + D C^{2}$ ，求 $∠ E A D$ 的度数；
问题拓展
（2）如图3，等边 $△ A B C$ 边长为6， $A E$ 绕点A逆时针旋转 $120 °$ 得 $A E^{'}$ ， N为 $A C$ 与 $B E^{'}$ 的交点，M为 $A B$ 的中点，当E在 $B C$ 边上运动时，请直接写出 $M N$ 的最小值．

查看解析
13、如图是由小正方形组成的7×7网格，每个小正方点叫做格点． $A ， B ， C$ 三点在格点，点D在 $A C$ 上，仅用无刻度的直尺在给定网格中完成画图．

(1)、在图1中，先画 $△ A B C$ 的 $∠ A$ 平分线 $A E$ ，再将 $△ A B C$ 绕点A旋转，使得旋转后的三角形的顶点都是格点，画出旋转后的三角形；

(2)、在图2中，先画点G，使四边形 $A C B G$ 为平行四边形，再在 $B G$ 上画点H，使 $∠ D H G = ∠ C H B$ ．

查看解析
14、如图， $A B$ 是半圆O的直径，C是 $A B$ 上一点，过点C作弦 $A D$ 的垂线，垂足为E， $C E = D E$ ．

(1)、求证：C是 $\overset{⌢}{A B}$ 的中点；

(2)、若 $B D = D E$ ，半圆O的半径为 $\sqrt{10}$ ，求 $C E$ 的长．

查看解析
15、为了庆祝祖国75岁华诞，小红制作了一副《盛世华章》的手工刺绣，如图该作品是一个长 $60 c m$ ，宽 $40 c m$ 的矩形，小红想将此作品装裱到四周宽度相同的相框里，制成一副矩形挂图，若要使整个挂图的面积是 $3500 {c m}^{2}$ ，求相框的宽度？

查看解析
16、如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，将 $△ A B C$ 绕点B逆时针旋转得到 $△ F B E$ ，点C，A的对应点分别为点E、F，点E落在 $B A$ 上，连接 $A F$ ．若 $∠ B A C = 24 °$ ．求 $∠ A F E$ 的度数．

查看解析
17、如图，在平行四边形 $A B C D$ 中，将 $A B$ 绕A逆时针旋转到 $A B^{'}$ ， $∠ B A B^{'}$ 的角平分线经过 $B C$ 的中点E，且 $B^{'} C = \frac{1}{2} B C$ ， $∠ D A B^{'} = \frac{1}{2} ∠ B^{'} B C$ ，则 $\frac{A B}{B C}$ 的值为．

查看解析
18、抛物线 $y = a x^{2} + b x + c (a < 0)$ 与x轴交于 $A (- 3, 0)$ ， B两点，与y轴交于点C，点 $(m - 6, n)$ 与点 $(4 - m, n)$ 也在该抛物线上，下列结论：①点B的坐标为 $(1, 0)$ ；②方程 $a x^{2} + b x + c + 2 = 0$ 有两个不相等的实数根；③ $\frac{3}{4} a + c < 0$ ④当 $x = - t^{2} - 2$ （ $t$ 为常数）时， $y < c$ ．其中正确结论的序号是

查看解析
19、方程 $(3 x + 1) (x - 3) + t^{2} = 0$ 总有两个相等的实数根，则t的值为

查看解析
20、如图（1），是中国传统园林建筑中的月亮门，拱门的上部分是圆的一段弧．随着四季更迭，半遮半掩之间，便将丝丝景致幻化成诗情画意．图（2）是月亮门的示意图，弦 $A B$ 长 $2 m$ ，拱高 $C D$ 长 $3 m$ ，则该拱门的半径是m．

查看解析

上一页 912 913 914 915 916 下一页跳转

$x$	$\cdot \cdot \cdot$	$- 4$	$- 3$	$- 2$	$- 1$	1	2	3	4	$\cdot \cdot \cdot$
$y = \frac{1}{2} x^{2}$	$\cdot \cdot \cdot$	8	4.5	2	0.5	0.5	2	4.5	8	$\cdot \cdot \cdot$
$x$	$\cdot \cdot \cdot$	$- 2$	$- 1.5$	$- 1$	$- 0.5$	0.5	1	1.5	2	$\cdot \cdot \cdot$
$y = 2 x^{2}$	$\cdot \cdot \cdot$	8	4.5	2	0.5	0.5	2	4.5	8	$\cdot \cdot \cdot$