相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、某林业局将一种树苗移植成活的情况绘制成如统计图,由此可估计这种树苗移植成活的概率约为( )
 A、0.95 B、0.90 C、0.85 D、0.80
A、0.95 B、0.90 C、0.85 D、0.80 -
2、如图1,是的直径,点D为下方上一点,点C为弧的中点,连结 , , .
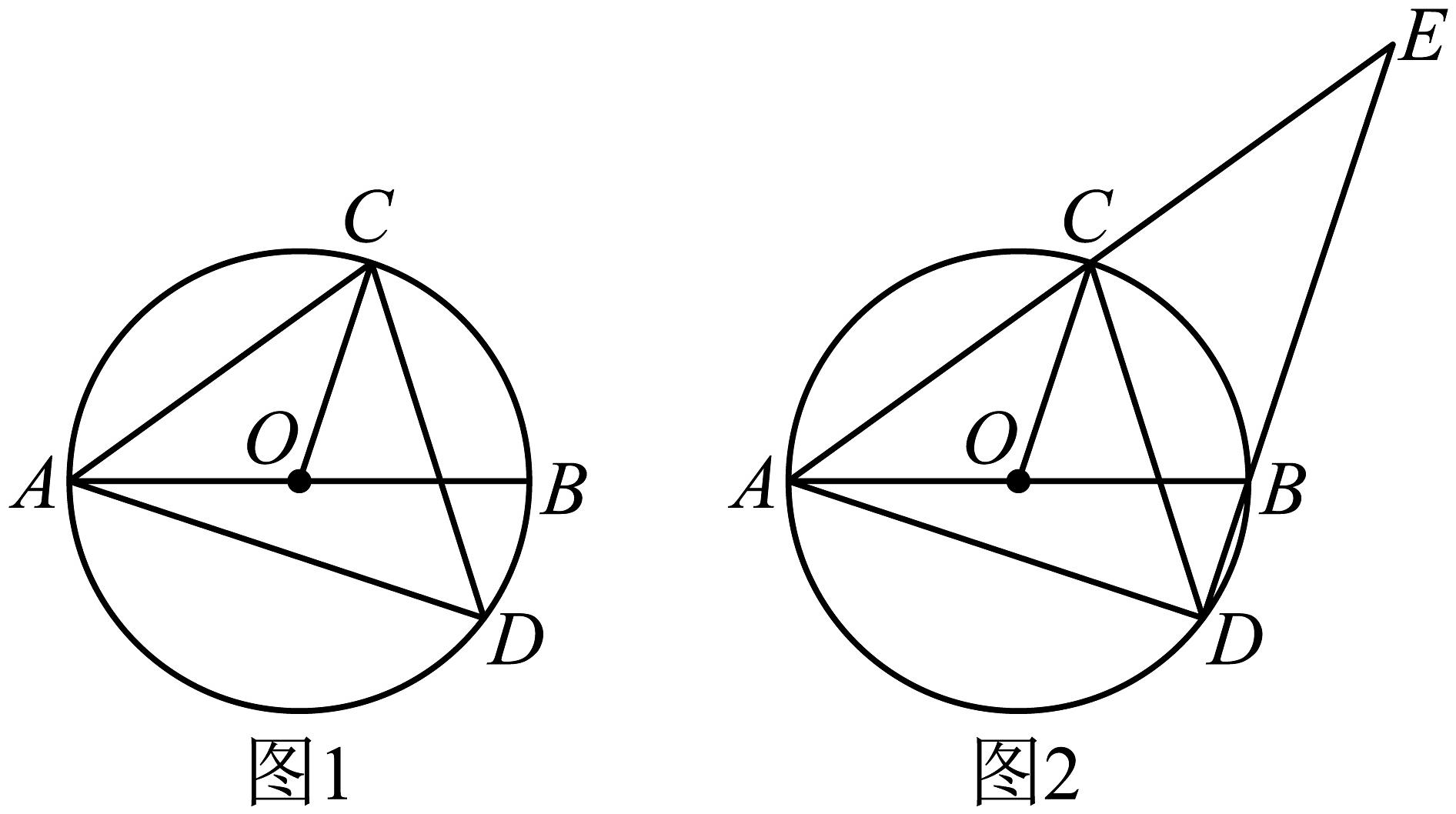 (1)、求证:平分 .(2)、如图2,延长 , 相交于点E.
(1)、求证:平分 .(2)、如图2,延长 , 相交于点E.①求证: .
②若 , , 求的半径.
-
3、如何拟定运动员拍照记录的方案?
素材1
图1是单板滑雪运动员从大跳台滑雪场地滑出的场景,图2是跳台滑雪场地的横截面示意图.垂直于水平底面 , 点D到A之间的滑道呈抛物线型.已知 , , 且点B处于跳台滑道的最低处.
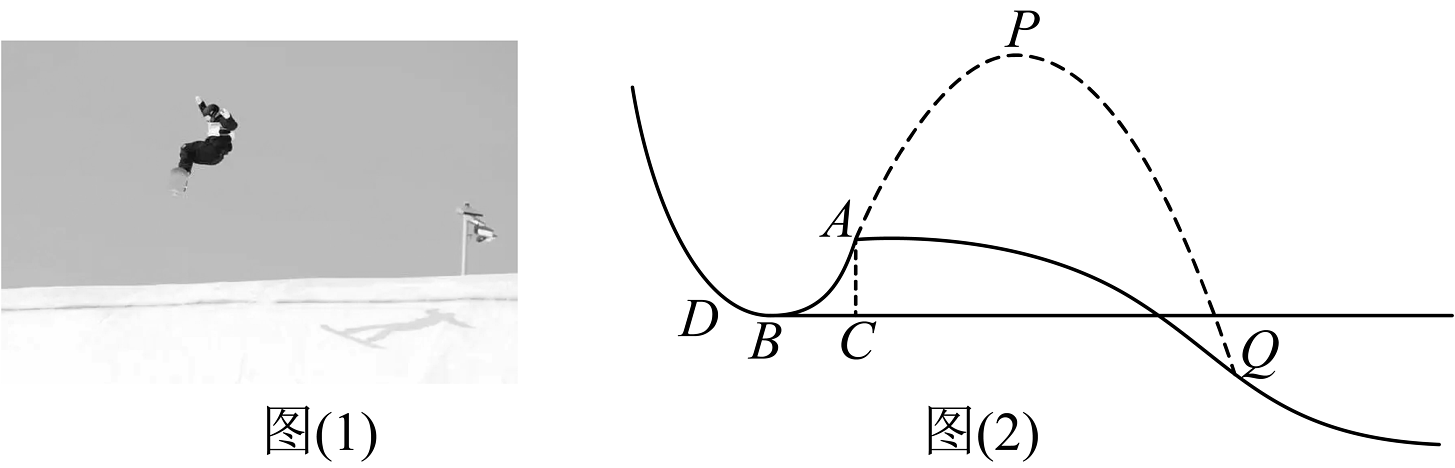
素材2
如图3,某运动员从点A滑出后的路径满足以下条件:
①运动员滑出路径与D、A之间的抛物线形状相同.
②该运动员在底面上方竖直距离处达到最高点P.
③落点Q在底面下方竖直距离 .

素材3
高速摄像机能高度还原运动员的精彩瞬间,如图4,有一台摄像机M进行跟踪拍摄:
①它与点B位于同一高度,且与点B距离;
②运动过程需在摄像头视角范围内才能记录,记摄像头的俯角为α;
③在平面直角坐标系中,设射线的解析式为 , 其比
例系数k和俯角α的函数关系如图5所示.
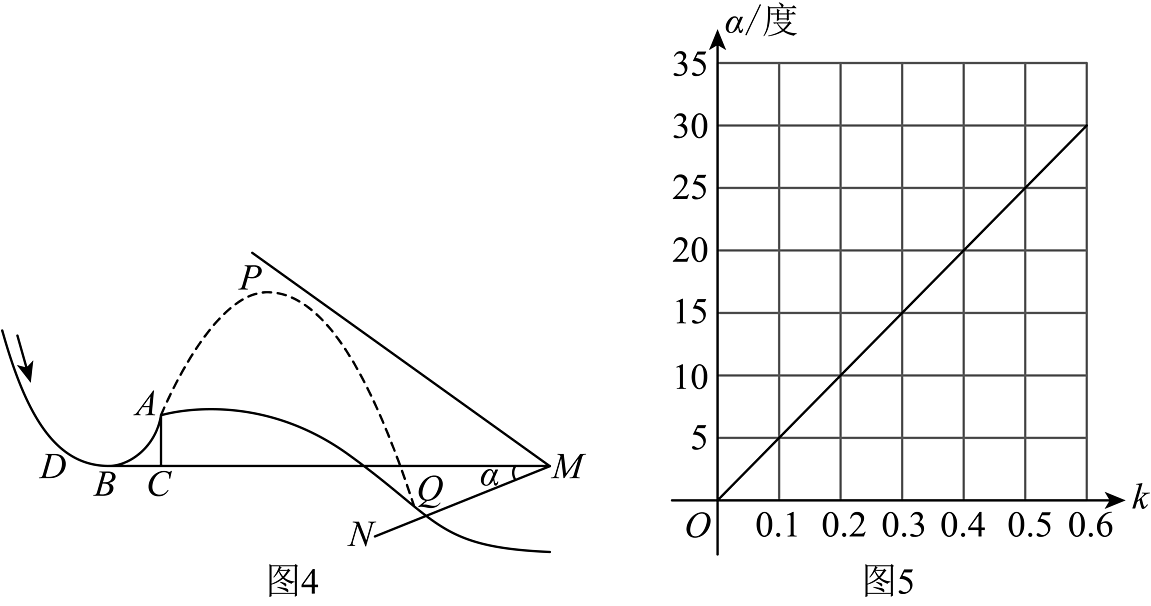
问题解决
任务1
确定D、A之间滑道的形状
在图2中建立适当的平面直角坐标系,求滑道所在抛物线的函数表达式.
任务2
确定运动员达到最高点的位置
在同一平面直角坐标系中,求运动员到达最高处时与点A的水平距离.
任务3
确定拍摄俯角α
若要求运动员的落点Q必须在摄像机M的视角范围内,则俯角α至少多少度(精确到个位)?
-
4、如图,在中, , 以为直径的分别交 , 于点 , , 连接交于点 .
 (1)、求证:;(2)、连接 , 若 , , 求的长.
(1)、求证:;(2)、连接 , 若 , , 求的长. -
5、在平面直角坐标系中,抛物线的顶点为 , 且过点 .(1)、求抛物线的函数表达式;(2)、求将抛物线向左平移几个单位,可使得平移后所得抛物线经过原点?
-
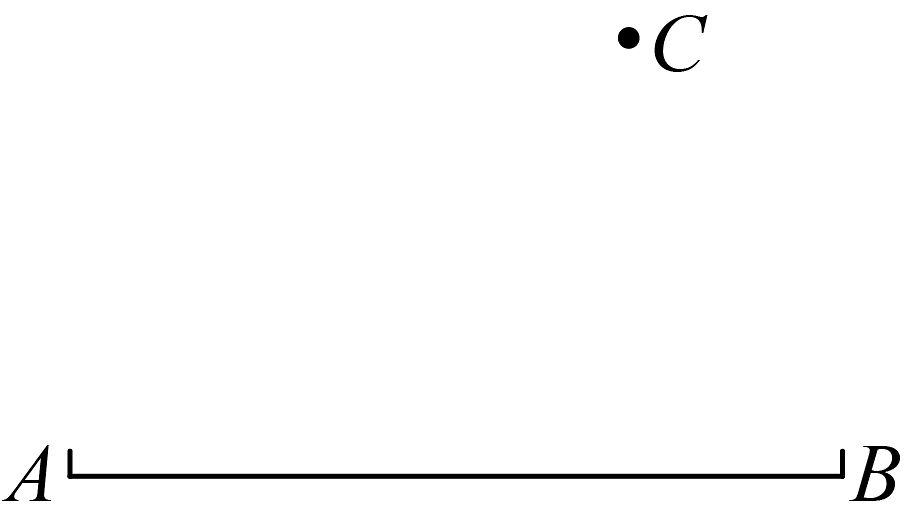
6、如图,以已知线段为弦作⊙O,使其经过已知点C.利用直尺和圆规作图(保留作图痕迹,不必写出作法).
-
7、如图所示,某建筑物有一抛物线形的大门,小滨想知道这道门的高度,他先测出门的宽度 , 然后用一根长为的小竹竿竖直的接触地面和门的内壁,并测得 , 则门高为( )
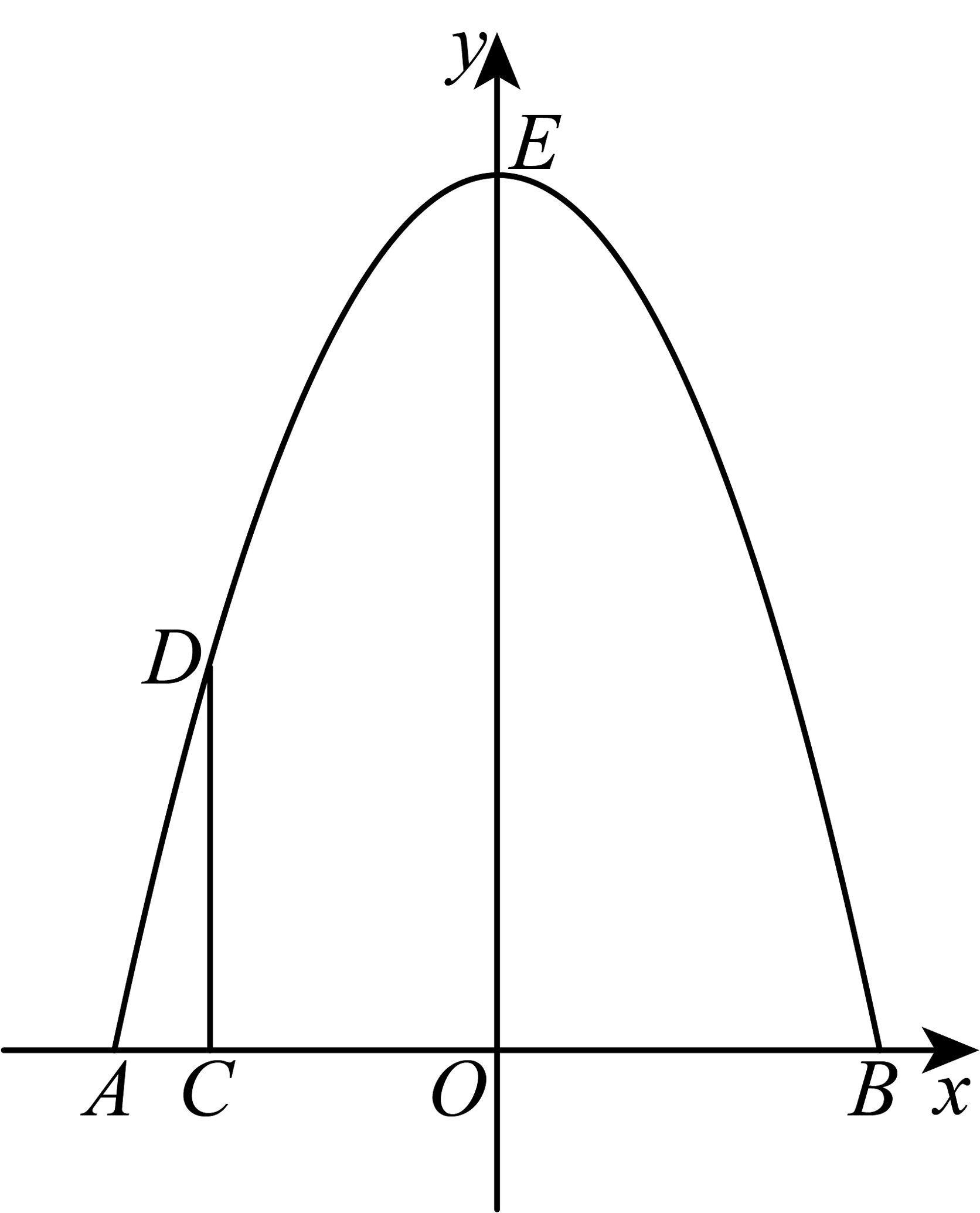 A、 B、 C、 D、
A、 B、 C、 D、 -
8、下列判断正确的是( )A、平分弦的直径垂直于弦 B、平分弦的直径必平分弦所对的两条弧 C、弦的垂直平分线必平分弦所对的两条弧 D、平分一条弧的直线必平分这条弧所对的弦
-
9、如图,的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将绕原点顺时针旋转后得到 , 则点的对应点的坐标是( )
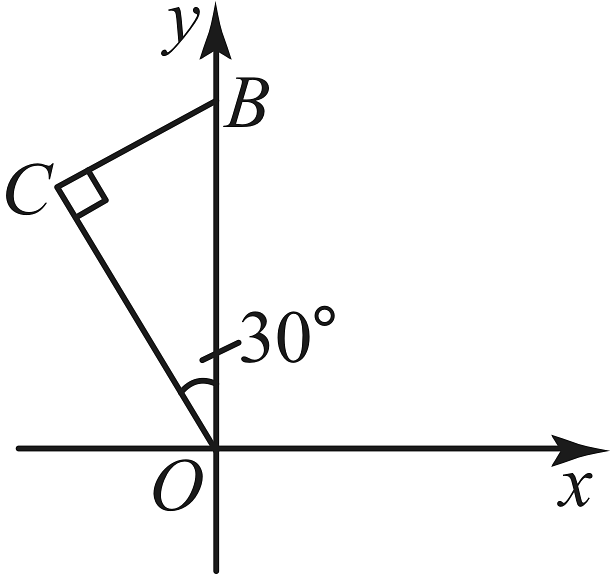 A、 B、 C、 D、
A、 B、 C、 D、 -
10、将抛物线的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为( )A、 B、 C、 D、
-
11、如图, , 则的度数是( )
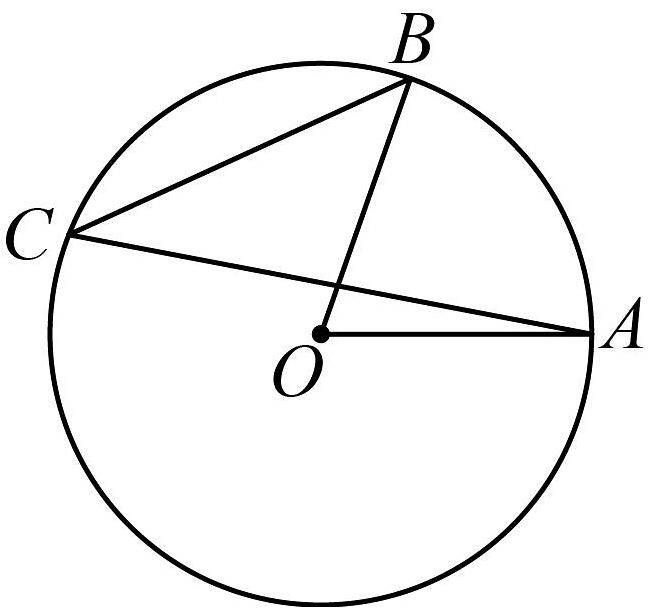 A、 B、 C、 D、
A、 B、 C、 D、 -
12、定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,那么称此图形为“手拉手全等模型”.例如,如图①,与都是等腰三角形,其中 , 则 .
 (1)、如图②,与都是等腰三角形, , , 且 , 求证: .(2)、如图③若和均为等腰直角三角形, , 点A,D,E在同一条直线上,为中上的高,连接 , 求的度数以及线段 , , 之间的数量关系,并说明理由.(3)、如图④,在四边形中, , , , 求的长.
(1)、如图②,与都是等腰三角形, , , 且 , 求证: .(2)、如图③若和均为等腰直角三角形, , 点A,D,E在同一条直线上,为中上的高,连接 , 求的度数以及线段 , , 之间的数量关系,并说明理由.(3)、如图④,在四边形中, , , , 求的长. -
13、【问题提出】
(1)已知:如图1所示,于点D,于点E,点C在线段上, , 且 . 求证:
① .
② .
【问题解决】
(2)如图2所示,点D,C,E在直线l上,点A,B在l的同侧, , 若 , , 求的面积.

-
14、如图,已知是等边三角形, , , 分别是射线 , , 上的点,且 , 连结 , , .
 (1)、求证:;(2)、试判断的形状,并说明理由.
(1)、求证:;(2)、试判断的形状,并说明理由. -
15、如图,的延长线于点 , 于点 , 且 .
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
16、如图,点 , , , 在同一条直线上, , , . 求证:

-
17、如图,点D在上,点E在上,相交于点O.
 (1)、若 , 求的度数;(2)、试猜想与之间的关系,并证明你的猜想.
(1)、若 , 求的度数;(2)、试猜想与之间的关系,并证明你的猜想. -
18、在中,利用直尺(没有刻度)和圆规作图(要求保留作图痕迹,不必写出作法):
 (1)、作出边上的中线;(2)、作出的角平分线 .
(1)、作出边上的中线;(2)、作出的角平分线 . -
19、如图,在中, , 是的平分线,是边上的中线.若 . 则 .

-
20、根据数量关系列不等式:的3倍与的差大于2. .