相关试卷

1、下列各语句是真命题的是（）

A、三个角对应相等的三角形全等 B、等角对等边 C、等腰三角形的对称轴是顶角平分线 D、三角形任何两边的和大于第三边

查看解析
2、如果 $a > b$ ，那么下列结论一定正确的是( )

A、 $1 + a > 1 + b$ B、 $a - 3 < b - 3$ C、 $- 3 a > - 3 b$ D、 $a c > b c$

查看解析
3、已知三角形两边的长分别是 $3$ 和 $7$ ，则第三边的长可以是（）

A、 $3$ B、 $10$ C、 $6$ D、 $16$

查看解析
4、如图，直线 $l_{1}$ 的解析表达式为： $y = - 3 x + 3$ ，且 $l_{1}$ 与 $x$ 轴交于点 $D$ ，直线 $l_{2}$ 经过点 $A$ ， $B$ ，直线 $l_{1}$ ， $l_{2}$ 交于点 $C$ ．

(1)、求点D的坐标；

(2)、求直线 $l_{2}$ 的解析表达式；

(3)、求 $△ A D C$ 的面积；

(4)、在直线上存在异于点C的另一点P，使得 $△ A D P$ 与 $△ A D C$ 的面积相等，求点P的坐标．

查看解析
5、周末，张洋去某杨梅园摘杨梅，已知该杨梅园内的杨梅单价是每千克40元．为满足客户需求，该杨梅园现推出两种不同的销售方案：
甲方案：游客进园需购买30元的门票，采摘的杨梅按原价的七折收费；
乙方案：游客进园不需购买门票，采摘的杨梅在10千克以内按原价收费、超过10千克后，10千克部分按原价收费，超过部分按原价的五折收费．
设张洋的采摘量为 $x (x > 0)$ 千克，按甲方案所需总费用为 $y_{1}$ 元，按乙方案所需总费用为 $y_{2}$ 元．

(1)、当采摘量超过10千克时，分别求出 $y_{1}$ 、 $y_{2}$ 关于x的函数表达式；

(2)、若张洋的采摘量为30千克，选择哪种方案更划算?请说明理由．

查看解析
6、在 $Rt △ A B C$ 中， $A C = B C$ ，点D为 $A B$ 中点， $∠ G D H = 90 °$ ， $∠ G D H$ 绕点D旋转， $D G, D H$ 分别与边 $A C$ ， $B C$ 交于E，F两点，下列结论：
① $A E + B F = \frac{\sqrt{2}}{2} A B$ ；② $A E^{2} + B F^{2} = E F^{2}$ ；③ $S_{四边形 C E D F} = \frac{1}{2} S_{△ A B C}$ ；④ $△ D E F$ 始终为等腰直角三角形，其中正确的是

查看解析
7、如图，有一块直角三角形纸片，两直角边 $A C = 6 cm$ ， $B C = 8 cm$ ．现将直角边 $A C$ 沿直线 $A D$ 折叠，使它落在斜边 $A B$ 上，且与 $A E$ 重合，则 $C D$ 的长等于 $cm$ ．

查看解析
8、如图，直线 $y = x + 2$ 与直线 $y = a x + c$ 相交于点 $P (m, 3)$ ，则关于 $x$ 的不等式 $x + 2 \geq a x + c$ 的解集为．

查看解析
9、如图，在平面直角坐标系中，一动点自点 $A_{0} (- 1, 0)$ 处向上平移1个单位长度至点 $A_{1} (- 1, 1)$ 处，然后向右平移2个单位长度至点 $A_{2} (1, 1)$ 处，再向下平移3个单位长度至点 $A_{3} (1, - 2)$ 处，再向左平移4个单位长度至点 $A_{4} (- 3, - 2)$ 处……按此规律平移下去，若这点平移到点 $A_{2024}$ 处时，则点 $A_{2024}$ 的坐标是（）

A、 $(1013, 1012)$ B、 $(- 1013, 1012)$ C、 $(- 1013, - 1012)$ D、 $(- 1012, - 1013)$

查看解析
10、某种蜡烛燃烧的长度与燃烧时间成正比例关系．若点燃6分钟后，高度下降 $3.6 cm$ ，则长 $22 cm$ 的此种蜡烛点燃15分钟后，剩余蜡烛的长度为（）

A、 $11 cm$ B、 $12 cm$ C、 $13 cm$ D、 $14 cm$

查看解析
11、下面四幅作品分别代表“惊蛰”“谷雨”“立秋”“冬至”，其中是轴对称图形的是（）

A、 B、 C、 D、

查看解析
12、已知 $⊙ O$ 的半径为 $13 cm$ ，弦 $A B ∥ C D$ ， $A B = 24 cm$ ， $C D = 10 cm$ ，则 $A B$ 、 $C D$ 之间的距离为．

查看解析
13、用配方法把二次函数 $y = - 2 x^{2} - 4 x + 1$ 写成 $y = a {(x - h)}^{2} + k$ 的形式为．

查看解析
14、如图，O是正 $△ A B C$ 内一点， $O A = 3$ ， $O B = 4$ ， $O C = 5$ ，将线段 $B O$ 以点B为旋转中心逆时针旋转 $60 °$ 得到线段 $B O^{'}$ ，下列结论：① $△ B O^{'} A$ 可以由 $△ B O C$ 绕点B逆时针旋转 $60 °$ 得到；②点O与 $O^{'}$ 的距离为4；③ $∠ A O B = 150 °$ ；④四边形 $A O B O^{'}$ 面积 $= 6 + 4 \sqrt{3}$ ；⑤ $S_{△ A O C} + S_{△ A O B} = 6 + \frac{9}{4} \sqrt{3}$ ，其中正确的结论是（）

A、①③④⑤ B、①②③④ C、①②④⑤ D、①②③④⑤

查看解析
15、 $⊙ O$ 的半径为5， $M$ 是圆外一点， $M O = 6$ ， $∠ O M A = 30 °$ ，则弦 $A B$ 的长为（）

A、4 B、6 C、 $6 \sqrt{3}$ D、8

查看解析
16、下列二次函数的图象中，顶点在第二象限的是（）

A、 $y = {(x - 1)}^{2} + 3$ B、 $y = {(x - 1)}^{2} - 3$ C、 $y = {(x + 1)}^{2} + 3$ D、 $y = {(x + 1)}^{2} - 3$

查看解析
17、某研学小组在研究拱桥的过程中发现拱桥的轮廓线（图中的桥下沿虚线部分）一般为抛物线或圆形，于是他们根据所学知识分组测量数据来确定某一拱桥的轮廓线，并解决相关问题．
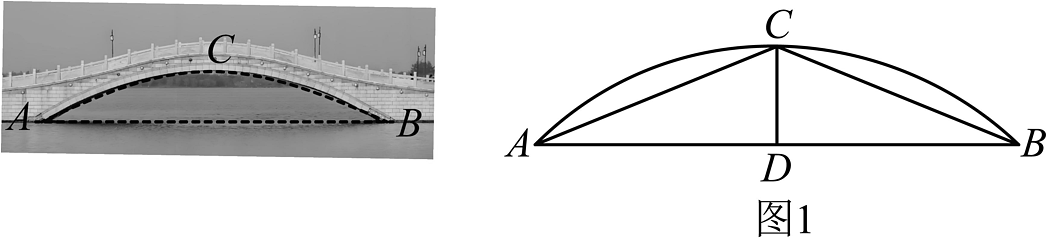
【实验操作】
如图1，第一小组在线段 $A B$ 的垂直平分线与轮廓线的最高点的交点 $C$ 处通过测量获得以下数据（单位：米）：
小组
线段 $1$
线段 $2$
线段 $3$
第一小组
$C D = 4$
$A C = 8$
$B C = 8$
任务1：请根据第一小组的数据求 $∠ A C B$ 的度数．
【建立模型】
如图 $2$ ，第二小组在轮廓线 $B C$ 段上选取 $E$ 点（不与 $B$ 、 $C$ 重合），在河边 $A$ 和 $B$ 处分别测量 $E$ 点的仰角，测量获得以下数据：
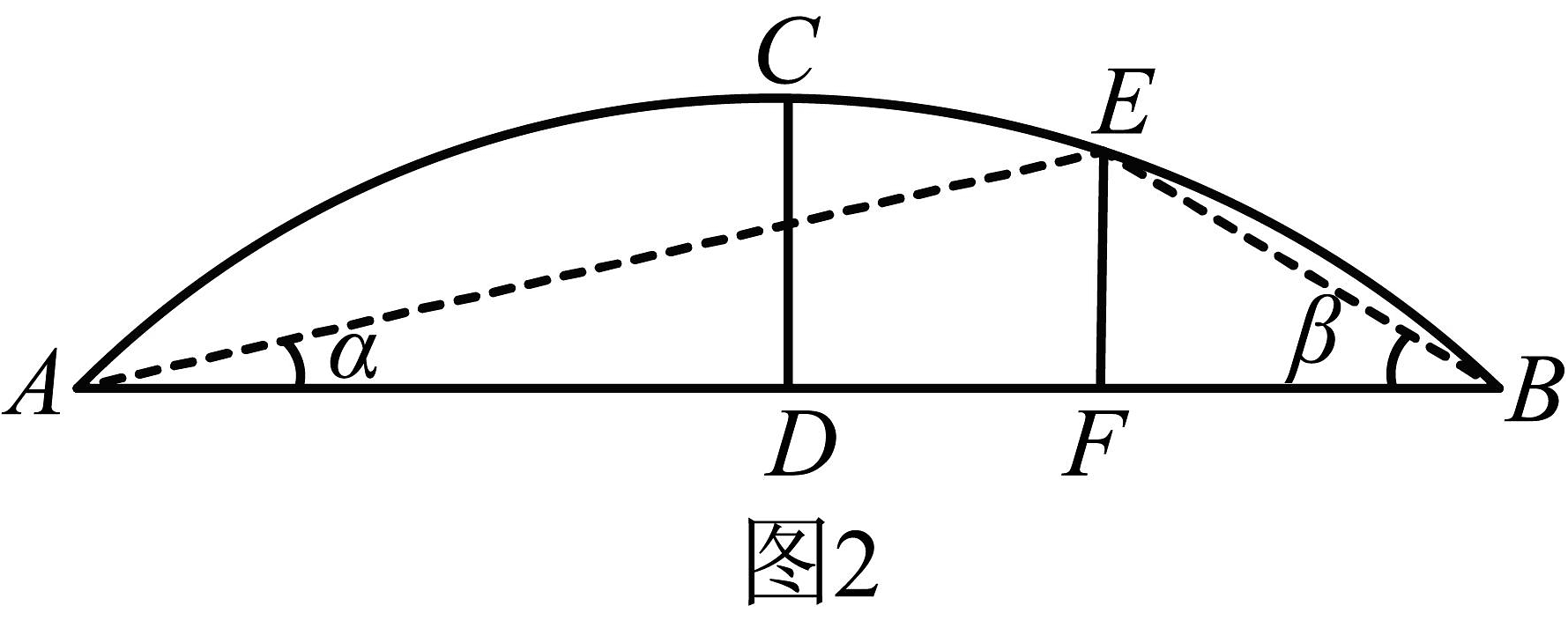
小组
$A$ 测 $E$ 仰角
$B$ 测 $E$ 仰角
第二小组
$∠ α = 13 °$
$∠ β = 32 °$
任务 $2$ ：根据所获得的数据，判断该拱桥轮廓线是抛物线还是圆形，请说明理由．
如果轮廓线是圆形，请求出圆的半径；如果轮廓线是抛物线，请建立适当的直角坐标系求抛物线的解析式．
【解决问题】
任务3：由于安全通行需要，现需要在拱桥上安装倒 $T$ 型的限高杆（如图 $3$ 中虚线部分），为了保证安装稳定，横杆两端和竖杆上端与桥体固定多出的部分长度均为 $\frac{1}{3}$ 米（横杆悬空的部分大于 $6$ 米），且横杆长度和竖杆长度之比为 $\frac{26}{5}$ ，那么此时横向限高杆离水面距离为多少米？（限高杆的宽度忽略不计）

查看解析
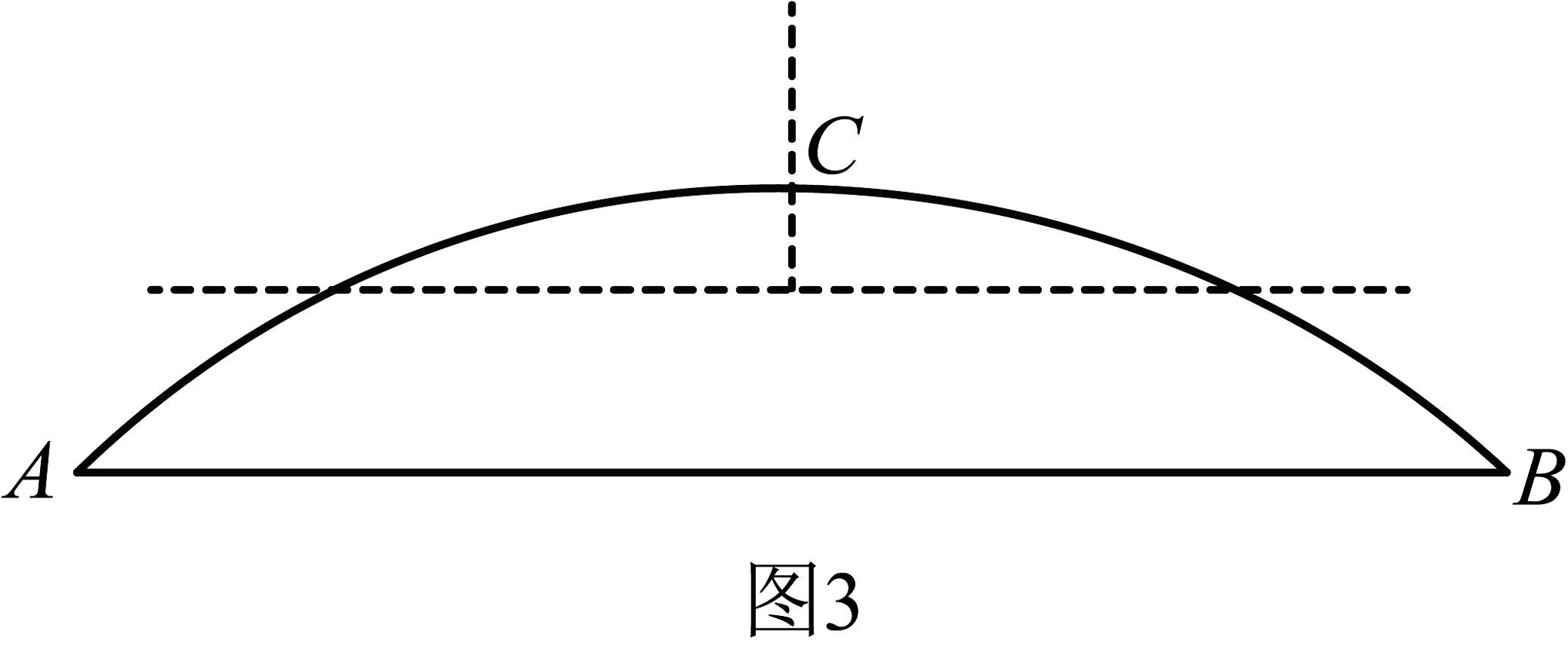
18、如图，在6×6的正方形网格中，点A，B，C均在格点上，请按要求作图．

(1)、在图1中画一个格点 $△ A D E$ ，使 $△ A D E ∽ △ A B C$ ．

(2)、在图2中画一条格点线段BP，交AC于点Q，使 $C Q = 2 A Q$ ．

查看解析
19、如图，点C是 $\overset{⌢}{A B}$ 上一点，且半径为2， $A C = B C$ ， $∠ A C B = 120 °$ ，点D在 $\overset{⏜}{B C}$ 上运动，连接 $A D$ 交 $B C$ 于点E，则 $\frac{D E}{A E}$ 的最大值＝．

查看解析
20、圆内接四边形 $A B C D$ 中， $∠ A : ∠ B : ∠ C = 2 : 3 : 7$ ，则 $∠ D =$ $° .$

查看解析

上一页 915 916 917 918 919 下一页跳转

小组	线段 $1$	线段 $2$	线段 $3$
第一小组	$C D = 4$	$A C = 8$	$B C = 8$

小组	$A$ 测 $E$ 仰角	$B$ 测 $E$ 仰角
第二小组	$∠ α = 13 °$	$∠ β = 32 °$