相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、 如图,在平面直角坐标系中,已知A(-1,0),B(0,2),将△ABO沿直线AB 翻折后得到△ABC.若反比例函数 0)的图象经过点C,则k=.

-
2、 如图,D 是等边三角形ABC 中边AB上的点,AD=2,BD=4.现将△ABC折叠,使得点C与点D 重合,折痕为EF,且点E,F分别在边 AC 和BC 上,则 .

-
3、 如图,已知矩形ABCD 的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD: AB=3:1,则点 C的坐标是.

-
4、 如图,△ABC为等边三角形,点D,E分别在边 BC,AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为 ( )
 A、1.8 B、2.4 C、3 D、3.2
A、1.8 B、2.4 C、3 D、3.2 -
5、如图,在平面直角坐标系中,四边形OABC是梯形CB∥OA,OC=BA,OA=7,BC=1,AB=5,P为x轴上的一个动点,点P 不与点O,A 重合.连结CP,过点 P 作PD 交AB 于点 D.
 (1)、直接写出点 B 的坐标:;(2)、当点 P 在线段OA 上运动时,使得∠CPD=∠OAB,且 BD:AD=3:2,则点 P的坐标为.
(1)、直接写出点 B 的坐标:;(2)、当点 P 在线段OA 上运动时,使得∠CPD=∠OAB,且 BD:AD=3:2,则点 P的坐标为. -
6、如图,E 是AB 的中点,AC=5, BD=2.若∠A=∠CED=∠B,则AB的长是 ( )
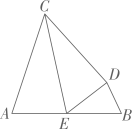 A、7 B、 C、 D、10
A、7 B、 C、 D、10 -
7、如图,正方形ABCD 的边长为4,E 是BC 上一点,过点E作EF⊥AE,交DC于点F,连结AF,则AF的最小值是( )
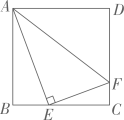 A、5 B、 C、2 D、3
A、5 B、 C、2 D、3 -
8、如图,已知点 A(0,4),B(4,1),BC⊥x轴于点C,点 P为线段OC上一点,且PA⊥PB,则点 P 的坐标为.

-
9、 根据收集的素材,探索完成任务.
探究太阳能热水器的安装 素材一 
太阳能热水器是利用绿
色能源造福人类的一项
发明.某品牌热水器主要
部件太阳能板需要安装
在每天都可以有太阳光照射到的地方,才能保证使用效果,否则不予安装.
素材二
某市位于北半球,太阳光线与水平线的夹角为α,冬至日时, 夏至日时, 参考数据: sin 14°≈0.24, 0.48, c os29°≈ 0. 87, tan29°≈ 0. 55; 0.93; sin 76°≈0. 97, cos76°≈0. 24,
索材三

如图,该市甲楼位于
乙楼正南方向,两楼
东西两侧都无法获得
太阳光照射.现准备
在乙楼南面墙上安装
该品牌太阳能板.已知两楼间距为54米,甲楼AB 共11层,乙楼CD 共15层,一层从地面起,每层楼高皆为3.3米. AE为某时刻的太阳光线.
问题解决
任务一
确定使用数据:要判断乙楼哪些楼层不能安装该品牌太阳能板,应选择 日(填“冬至”或“夏至”)时,α为 (填“14°”“29°”“43°”“76°”中的一个)进行计算.
任务二
探究安装范围:利用任务一中选择的数据进行计算,确定乙楼中哪些楼层不能安装该品牌太阳能热水器.
-
10、为积极响应绿色出行的号召,骑车出行已经成为当前的新风尚.图①是某品牌自行车放在水平地面上的实物图,图②是其部分示意图,其中AB∥CD∥l,车轮半径为 32 cm,∠ABC=64°,BC=60 cm,坐垫 E 与点 B的距离 BE 为 10 cm.
 (1)、求坐垫 E 到地面的距离;(2)、根据经验,当坐垫 E 到 CD 的距离调整为人体腿长的 时,坐骑比较舒适.小明的腿长约为84 cm,现将坐垫E调整至坐骑舒适的高度位置 E'处,求EE'的长.(结果精确到0.1 cm.参考数据: sin 64°≈0.90, cos 64°≈0.44, tan 64°≈2.05)
(1)、求坐垫 E 到地面的距离;(2)、根据经验,当坐垫 E 到 CD 的距离调整为人体腿长的 时,坐骑比较舒适.小明的腿长约为84 cm,现将坐垫E调整至坐骑舒适的高度位置 E'处,求EE'的长.(结果精确到0.1 cm.参考数据: sin 64°≈0.90, cos 64°≈0.44, tan 64°≈2.05) -
11、阅读与思考:
请仔细阅读并完成相应的任务.
利用我们所学习的三角函数的相关知识可以解决许多关于三角形边长、角度、面积等问题.如图,在锐角三角形 ABC中,∠A,∠ABC,∠C的对边分别是a,b,c,过点 B 作 BH⊥AC于点H,则 即AH= ccos A,于是CH=b-ccos A.在 Rt△ABH 中, AH2 , 在 Rt△BHC 中, 整理得

任务:
(1)、;.(2)、已知在△ABC 中,∠A,∠B,∠C 的对边分别是a,b,c, 求c. -
12、 如图,在△ABC 中,AD⊥BC 于点 D,AE 是 BC 边上的中线,AB=10,AD=6,tan∠ACB=1.
 (1)、求 BC的长;(2)、求 sin∠DAE 的值.
(1)、求 BC的长;(2)、求 sin∠DAE 的值. -
13、如图,点 B 位于点 A 的北偏东60°方向,距离2k m处,点 D在点 B 的正北方向,且在点A 的东北方向,则点 D 到点A 的距离为 km.

-
14、如图,在 Rt△ABC 中,∠C=90°, D为边AC上一点,∠BDC=45°,AD=7,则CD=.

-
15、如图,△ABC的顶点在边长为1的正方形网格的格点上.
 (1)、直接写出 cos B 和 tan(∠ACB-90°)的值;(2)、求 sin A 的值.
(1)、直接写出 cos B 和 tan(∠ACB-90°)的值;(2)、求 sin A 的值. -
16、方形网格中,已知点 A,B,C,D,O均在格点上,其中A,B,D又在⊙O 上,E 是线段CD 与⊙O的交点,则∠BAE 的正切值为.

-
17、如图,在4×5的网格中,每个小正方形的边长均为1.若△ABC的顶点都在格点上,则 sin C 的值为.

-
18、 如图是一架人字梯,已知AB=AC=2米,AC与地面 BC的夹角为α,则两梯脚之间的距离 BC为( )
 A、4cosα米 B、4sinα米 C、4tanα米 D、米
A、4cosα米 B、4sinα米 C、4tanα米 D、米 -
19、学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳AB到地面,如图所示.已知彩旗绳与地面形成25°角(即∠BAC=25°),彩旗绳固定在地面的位置与图书馆相距32 米(即AC=32米),则彩旗绳AB 的长度为( )
 A、32sin 25°米 B、32cos 25°米 C、米 D、米
A、32sin 25°米 B、32cos 25°米 C、米 D、米 -
20、 如图,某游乐场一山顶滑梯的坡角为α,高为h,则滑梯的长l为( )
 A、hsinα B、htanα C、 D、
A、hsinα B、htanα C、 D、