相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、 如图,四边形 ABCD 的对角线AC,BD相交于点O,OA=OC,AD∥BC,则下列说法错误的是 ( )
 A、若AC=BD,则四边形ABCD 是矩形 B、若 BD 平分∠ABC,则四边形 ABCD 是菱形 C、若AB⊥BC且AC⊥BD,则四边形ABCD是正方形 D、若AB=BC且AC⊥BD,则四边形ABCD是正方形
A、若AC=BD,则四边形ABCD 是矩形 B、若 BD 平分∠ABC,则四边形 ABCD 是菱形 C、若AB⊥BC且AC⊥BD,则四边形ABCD是正方形 D、若AB=BC且AC⊥BD,则四边形ABCD是正方形 -
2、 如图,P 是正方形ABCD 的对角线BD上一动点(不与点 B,D 重合),PE⊥DC,PF⊥BC,垂足分别为E,F.
 (1)、求证:四边形 FCEP 为矩形;(2)、求证:四边形 FCEP 的周长是定值:(3)、求证:PA=EF;(4)、在点 P 的运动过程中,EF 的长也随之变化,若正方形 ABCD 的边长为2,求 EF 长的最小值.
(1)、求证:四边形 FCEP 为矩形;(2)、求证:四边形 FCEP 的周长是定值:(3)、求证:PA=EF;(4)、在点 P 的运动过程中,EF 的长也随之变化,若正方形 ABCD 的边长为2,求 EF 长的最小值. -
3、如图
 (1)、如图①,在正方形 ABCD 中,E为BD 上一点 连结AE,CE,则AE 与CE 的数量关系为;(2)、如图②,若EA=EM,判断ME 与 EC 的位置关系,并说明理由;(3)、如图③,过点 E 作 ME⊥EC交AD 于点 M,请判断EA 与 EM的数量关系,并说明理由.
(1)、如图①,在正方形 ABCD 中,E为BD 上一点 连结AE,CE,则AE 与CE 的数量关系为;(2)、如图②,若EA=EM,判断ME 与 EC 的位置关系,并说明理由;(3)、如图③,过点 E 作 ME⊥EC交AD 于点 M,请判断EA 与 EM的数量关系,并说明理由. -
4、如图,▱ABCD的对角线AC,BD交于点 O,分别以点 B,C 为圆心, AC, BD长为半径画弧,两弧交于点 P,连结 BP,CP.
 (1)、试判断四边形 BPCO 的形状,并说明理由;(2)、请说明当▱ABCD 的对角线满足什么条件时,四边形 BPCO是正方形?
(1)、试判断四边形 BPCO 的形状,并说明理由;(2)、请说明当▱ABCD 的对角线满足什么条件时,四边形 BPCO是正方形? -
5、如图,在菱形ABCD 中,点 P 在对角线 BD 上,过点 P 分别作CD,BC的平行线交 BC,CD于点E,F.
 (1)、求证:AB=PE+PF;(2)、连结AP,若∠ABC=60°,∠APE=150°,判断 PE 与 PF 的数量关系,并说明理由.
(1)、求证:AB=PE+PF;(2)、连结AP,若∠ABC=60°,∠APE=150°,判断 PE 与 PF 的数量关系,并说明理由. -
6、如图,在△ABC中,∠BAC=90°,D 是 BC的中点,分别过点A,D 作 BC,BA的平行线交于点 E,且 DE 交 AC 于点 O,连结CE,AD.
 (1)、求证:四边形ADCE是菱形;(2)、若 求四边形ADCE的面积.
(1)、求证:四边形ADCE是菱形;(2)、若 求四边形ADCE的面积. -
7、如图,在菱形ABCD中,F是CD上一动点,过点F作FG⊥AC交BC于点G,垂足为E,连结AF,AG.
 (1)、求证:AF=AG;(2)、当∠DAB = 100°,AF =AD 时,试求∠AFG的度数.
(1)、求证:AF=AG;(2)、当∠DAB = 100°,AF =AD 时,试求∠AFG的度数. -
8、 如图,有一张矩形纸片 ABCD,在AD边上取一点 P,沿BP 翻折,使点 A 落在矩形内部点 A'处;再次翻折矩形,使点 D 落在PA'上的点 D'处,折痕为 PE,则∠BPE的度数为.

-
9、 如图,延长矩形 ABCD 的边 BC 至点E,使CE=BD,连结 AE.若∠ABD=60°,则∠E= ( )
 A、45° B、30° C、20° D、15°
A、45° B、30° C、20° D、15° -
10、已知:如图0,将矩形纸ABCD 的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形 EFGH.
 (1)、求证:四边形 EFGH 是矩形;(2)、若EH=3 cm,EF=4 cm,求边 AD的长.
(1)、求证:四边形 EFGH 是矩形;(2)、若EH=3 cm,EF=4 cm,求边 AD的长. -
11、如图,在矩形ABCD 中,E,F是边 BC上两点,且 BE=EF=FC,连结DE,AF,DE 与AF 相交于点 G,连结 BG.若AB=4,BC=6,则sin∠GBF的值为 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、 如图,在菱形ABCD 中,对角线 AC,BD 交于点O,添加条件: , 可使菱形 ABCD 成为正方形.

-
13、如图,正方形 ABCD 的对角线交于点O,则图中共有个等腰直角三角形.

-
14、
定义
有一组邻边相等,并且有一个角是的平行四边形叫做正方形
性质
正方形的四条边相等
正方形的四个角都是
正方形的对角线相等,并且互相垂直平分,每条对角线平分一组对角(即对角线与边的夹角等于45°).
正方形既是轴对称图形又是中心对称图形,对称轴有四条,对称中心是
判定
有一个角是直角,且有一组邻边相等的平行四边形是正方形
有一组邻边相等的矩形是正方形
有一个角是直角的菱形是正方形
-
15、如图, □ABCD 的对角线AC,BD交于点 O,以下条件不能证明□AB-CD 是菱形的是( )
 A、∠BAC=∠BCA B、∠ABD=∠CBD C、 D、
A、∠BAC=∠BCA B、∠ABD=∠CBD C、 D、 -
16、 如图,在菱形 ABCD中,对角线AC,BD相交于点O,过点 A 作AE⊥BC,垂足为 E,交 BD 于点F.若AC=6,BD=8.
 (1)、菱形 ABCD 的面积为;(2)、AB= , AE= ;(3)、BF=.
(1)、菱形 ABCD 的面积为;(2)、AB= , AE= ;(3)、BF=. -
17、
定义
有一组的平行四边形叫做菱形
性质
菱形的四条边都
菱形的对角线互相平分,并且每条对角线平分
菱形是轴对称图形,所在的直线是它的对称轴
菱形是中心对称图形,它的对称中心是
判定
定义法
四条边相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
结论
菱形的面积=底×高
菱形的面积等于乘积的一半
菱形的两条对角线将其分成四个直角三角形,且四个直角三角形的面积相等
-
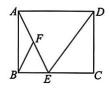
18、 如图,在矩形ABCD 中,点E在边 BC 上,F 是 AE 的中点,AB=8,AD=DE=10,则 BF 的长为.
-
19、 如图,在矩形ABCD中,对角线AC,BD 相交于点O,∠ABD=60°,AB=2,则AC的长为( )
 A、6 B、5 C、4 D、3
A、6 B、5 C、4 D、3 -
20、已知四边形 ABCD 是平行四边形,下列条件中,不能判定▱ABCD为矩形的是( )A、∠A=90° B、∠B=∠C C、AC=BD D、AC⊥BD