相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、 如图,水暖管横截面是圆,半径r=5mm的水暖管有积水(阴影部分),水面的宽度AB 为8 mm,则积水的最大深度 CD(CD<r)是mm.

-
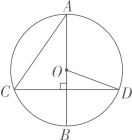
2、如图,AB是⊙O的直径,弦CD⊥OA 于点 E,连结OC,OD.若⊙O的半径为m,∠AOD=α,则下列结论一定成立的是 ( )
 A、OE=m·tanα B、CD=2m·sinα C、AE=m·cosα D、
A、OE=m·tanα B、CD=2m·sinα C、AE=m·cosα D、 -
3、 如图3,四边形 ABCD是⊙O的内接四边形,BE是⊙O的直径,连结 CE,DE.若∠BAD=110°,则∠DCE=°.

-
4、 如图,AB 是半圆O的直径,∠BAC=30°,则∠D 的度数是( )
 A、130° B、125° C、120° D、115°
A、130° B、125° C、120° D、115° -
5、
性质
圆内接四边形的对角
圆内接四边形的任意一个外角等于它的内对角
-
6、如图,点 A,B,C 在⊙O上,C 为. 的 中 点.若∠BAC = 2 ∠OAB, 则∠AOB等于( )
 A、144° B、135° C、130° D、120°
A、144° B、135° C、130° D、120° -
7、 如图,在⊙O中,△AOB 是 正 三 角形,点 C 在 上.若∠CAB=20°,则∠ABC=( )
 A、10° B、15° C、20° D、25°
A、10° B、15° C、20° D、25° -
8、
定义
顶 点 在 , 并且 两 边 都 和 圆的角叫做圆周角
圆周角定理
圆周角的度数等于它所对弧上的圆心角度数的一半
圆周角定理的推论
半圆(或直径)所对的圆周角是;90°的圆周角所对的弦是
在同圆或等圆中,同弧或等弧所对的圆周角;相等的圆周角所对的弧也
防错提醒
圆的一条弧(弦)只对着一个圆心角,所对的圆周角有无数个;一条弧所对的圆周角的度数只有一个,而一条弦所对的圆周角的度数有两个,这两个度数的和为180°
-
9、 如图,AB,AC 是⊙O 的两条弦,OD⊥AB 于点D,OE⊥AC 于点E,连结OB,OC.若∠DOE=140°,则∠BOC的度数为 ( )
 A、70° B、80° C、90° D、100°
A、70° B、80° C、90° D、100° -
10、 如图,AB是⊙O的直径, ∠COD=35°,则∠AOE的度数为 .

-
11、 如图,AB 是半圆O的直径,弦CD∥AB,CD=8,弦CD与直径AB 之间的距离为3,则AB=.

-
12、 如图,在⊙O中,点 C 在弦AB 上,连结OB,OC.若OB=5,AC=1,BC=5,则线段OC的长为.

-
13、如图,⊙O的直径CD垂直弦AB于点E,且CE=3,DE=7,则AE=( )
 A、4 B、2 C、 D、
A、4 B、2 C、 D、 -
14、 如图,在⊙O 中,已知直径AB⊥弦CD,∠BOD=70°,那么∠BAC的度数等于( )
 A、55° B、45° C、35° D、25°
A、55° B、45° C、35° D、25° -
15、
垂径定理
垂直于弦的直径 , 并且平分弦所对的弧
推论
平分弦(不是直径)的直径垂直于弦,并且平分
平分弧的直径弧所对的弦
-
16、
确定圆的条件
不在同一条直线上的三个点确定一个圆
三角形的外心
三角形三条边的的交点,即为三角形外接圆的圆心
防错提醒
锐角三角形的外心在三角形的内部,直角三角形的外心为直角三角形的斜边中点,钝角三角形的外心在三角形的外部
-
17、
圆
在同一平面内,线段 OP 绕它固定的一个端点O 旋转一周,另一端点 P 所经过的封闭曲线叫做圆.定点O叫做圆心,线段OP 叫做圆的半径
弦
连结圆上任意两点的叫做弦
直径
经过圆心的弦叫做直径
弧
圆上任意两点间的部分叫做圆弧,简称弧
半圆
圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆
优弧
大于半圆的弧叫做优弧
劣弧
小于半圆的弧叫做劣弧
-
18、 问题情境:
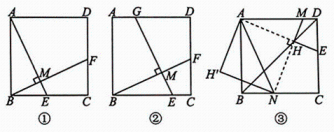
如图①,在正方形ABCD中,点E,F分别在边 BC,CD 上,且 AE⊥BF,垂足为 M,那么 AE 与BF 相等吗?
 (1)、直接判断:AE BF(填“=”或“≠”);在“问题情境”的基础上,继续探索:(2)、问题探究:
(1)、直接判断:AE BF(填“=”或“≠”);在“问题情境”的基础上,继续探索:(2)、问题探究:如图②,在正方形ABCD中,点E,F,G分
别在边 BC,CD 和 DA 上,且 GE⊥BF,垂足为M,那么 GE 与 BF 相等吗?请证明你的结论;
(3)、问题拓展:如图③,点 E在边 CD 上,且 MN⊥AE,垂足为H,当点 H在正方形ABCD 的对角线BD上时,连结AN,将△AHN沿AN 翻折,点 H落在点 H'处.四边形AHNH'是正方形吗?请说明理由.
-
19、 如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF 相交于点G,H 为BF 的中点,连结GH,则GH 的长为.

-
20、 如图,在正方形ABCD中,点E,F分别在边CD,AD 上,BE⊥CF于点G,若BC=8,AF=2,则GF的长为.
