相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、已知关于的一元二次方程 .(1)、证明:无论取何值,此方程总有两个实数根;(2)、若方程有两个不相等的实数根分别为 , 且 , 求的值.
-
2、如图,在平面直角坐标系中,已知△ABC的顶点的坐标分别是A(﹣5,2),B(﹣2,4),C(﹣1,1).

(1)在图中作出△A1B1C1 , 使△A1B1C1和△ABC关于x轴对称;
(2)画出将△ABC以点O为旋转中心,顺时针旋转90°对应的△A2B2C2;
(3)直接写出点B关于点C的对称点的坐标.
-
3、在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .

-
4、如图,是直径,、是上的两点,且 , 连接和 , 下列四个结论中:①;②垂直平分;③;④ . 所有正确结论的序号是 .

-
5、如图,点分别在正方形的边上,且 . 把绕点顺时针旋转得到 . 若 , 则的长度为 .

-
6、已知二次函数的图象如图所示,对称轴为直线 , 有下列6个结论:①;②;③;④;⑤方程有两个相等的实数根;⑥当时,随的增大而减小.其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
7、如图, , 分别与相切于 , 两点,点为上异于点 , 的一点.若 , 则的度数为( )
 A、 B、 C、 D、或
A、 B、 C、 D、或 -
8、若为二次函数的图象上的三点,则 , 的大小关系是( )A、 B、 C、 D、
-
9、已知关于的一元二次方程有实数根,则系数的取值范围是( )A、 B、 C、且 D、且
-
10、平面直角坐标系中,与点关于原点对称的点的坐标是( )A、 B、 C、 , D、
-
11、围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.下面是对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、
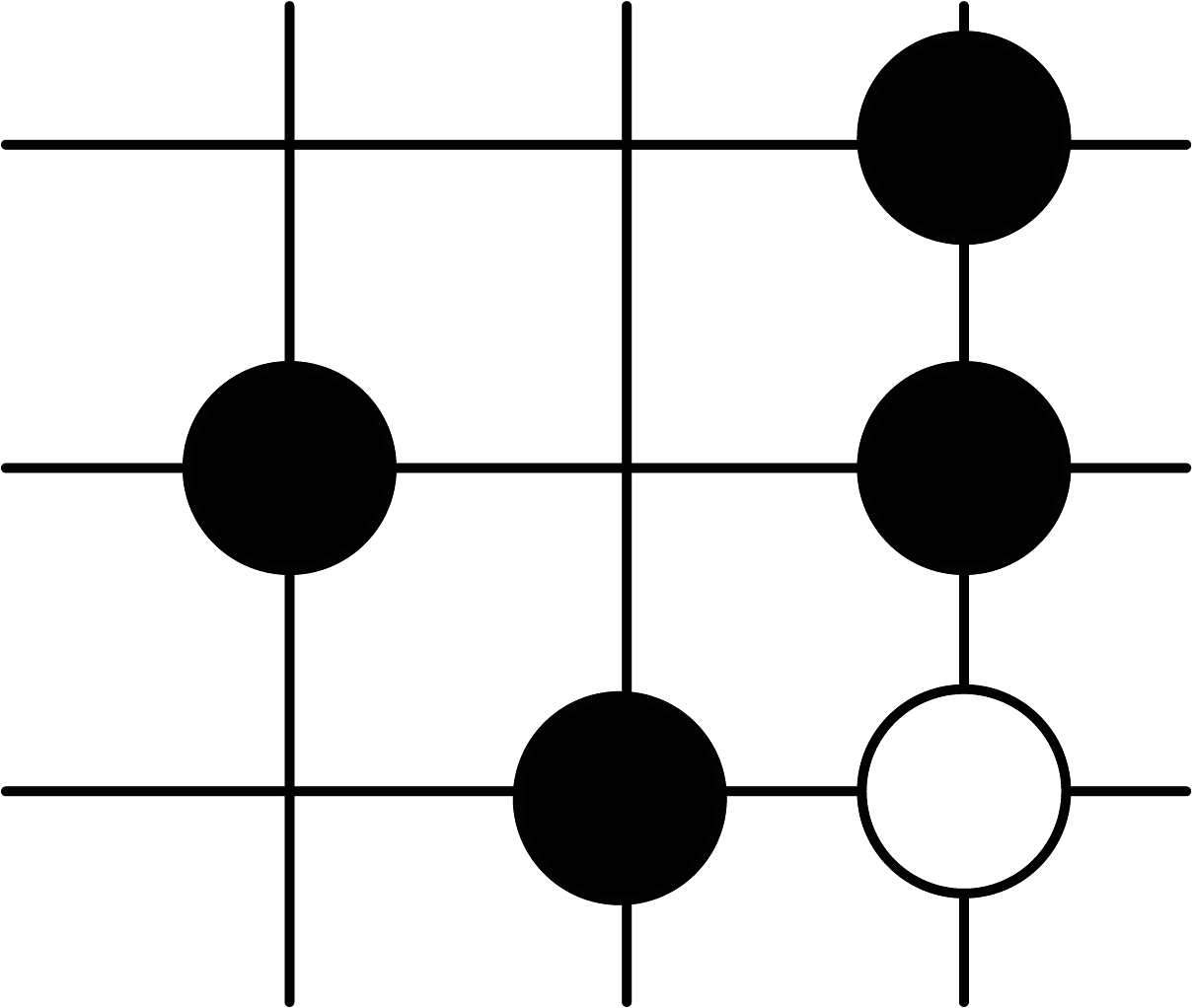 B、
B、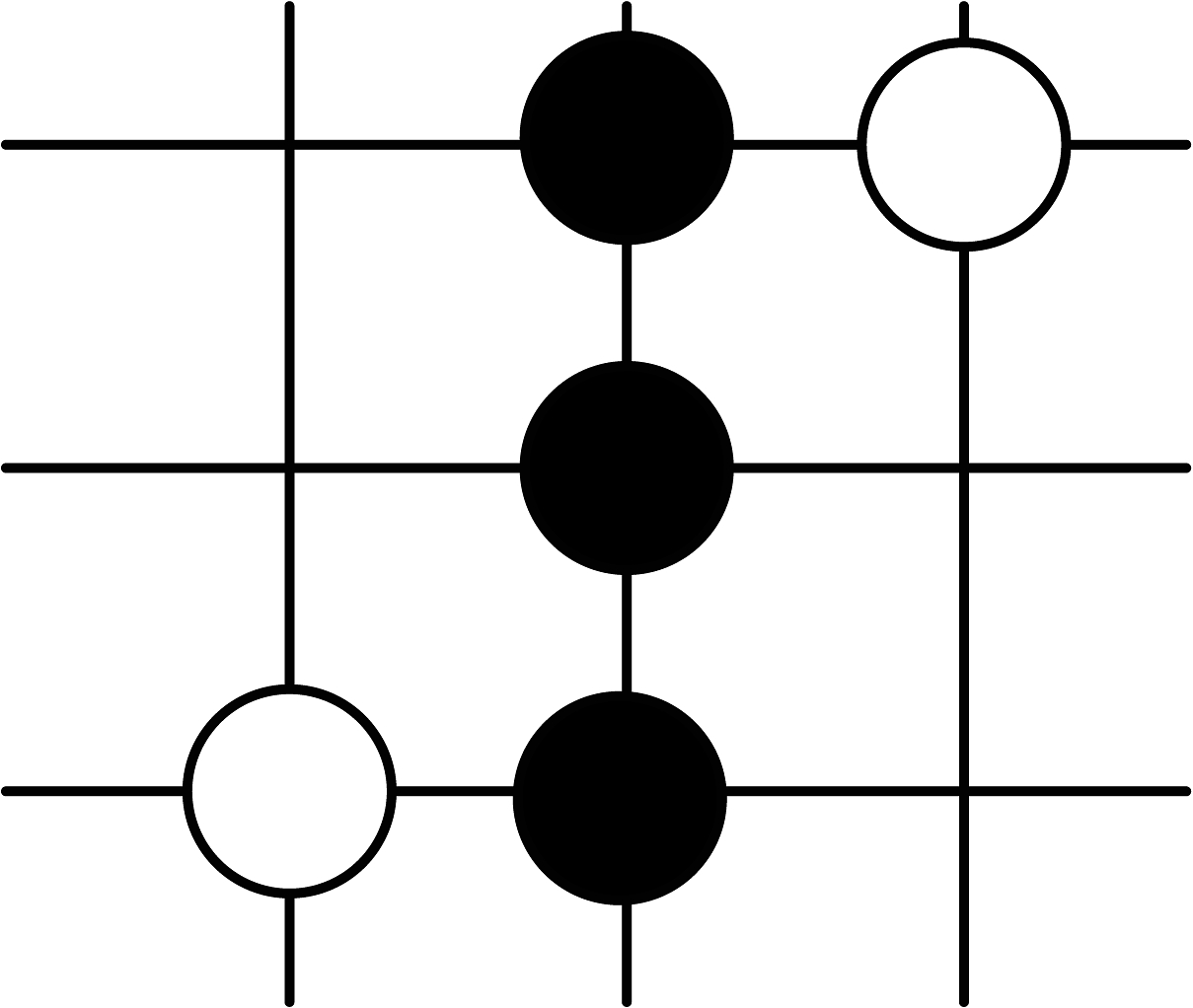 C、
C、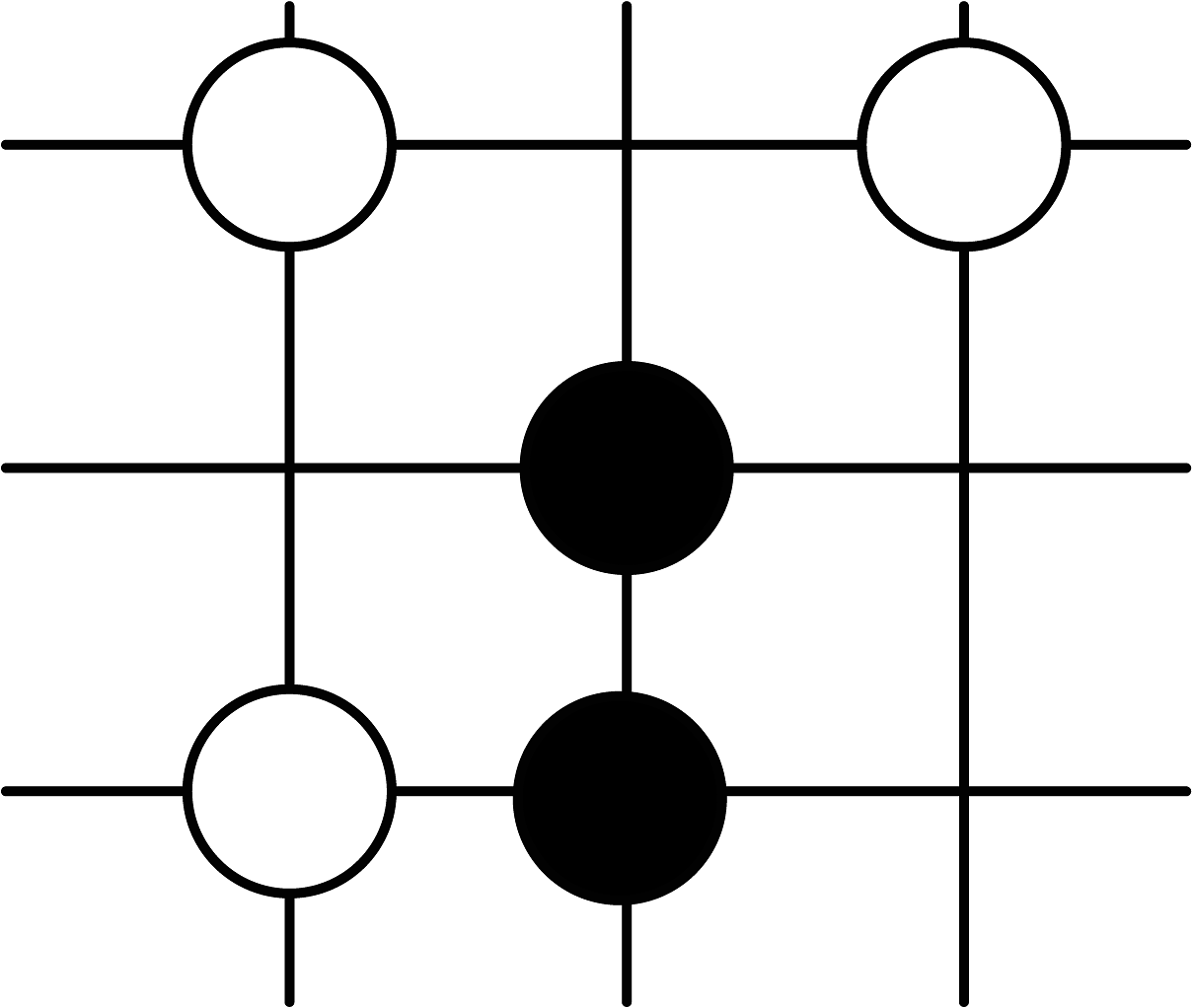 D、
D、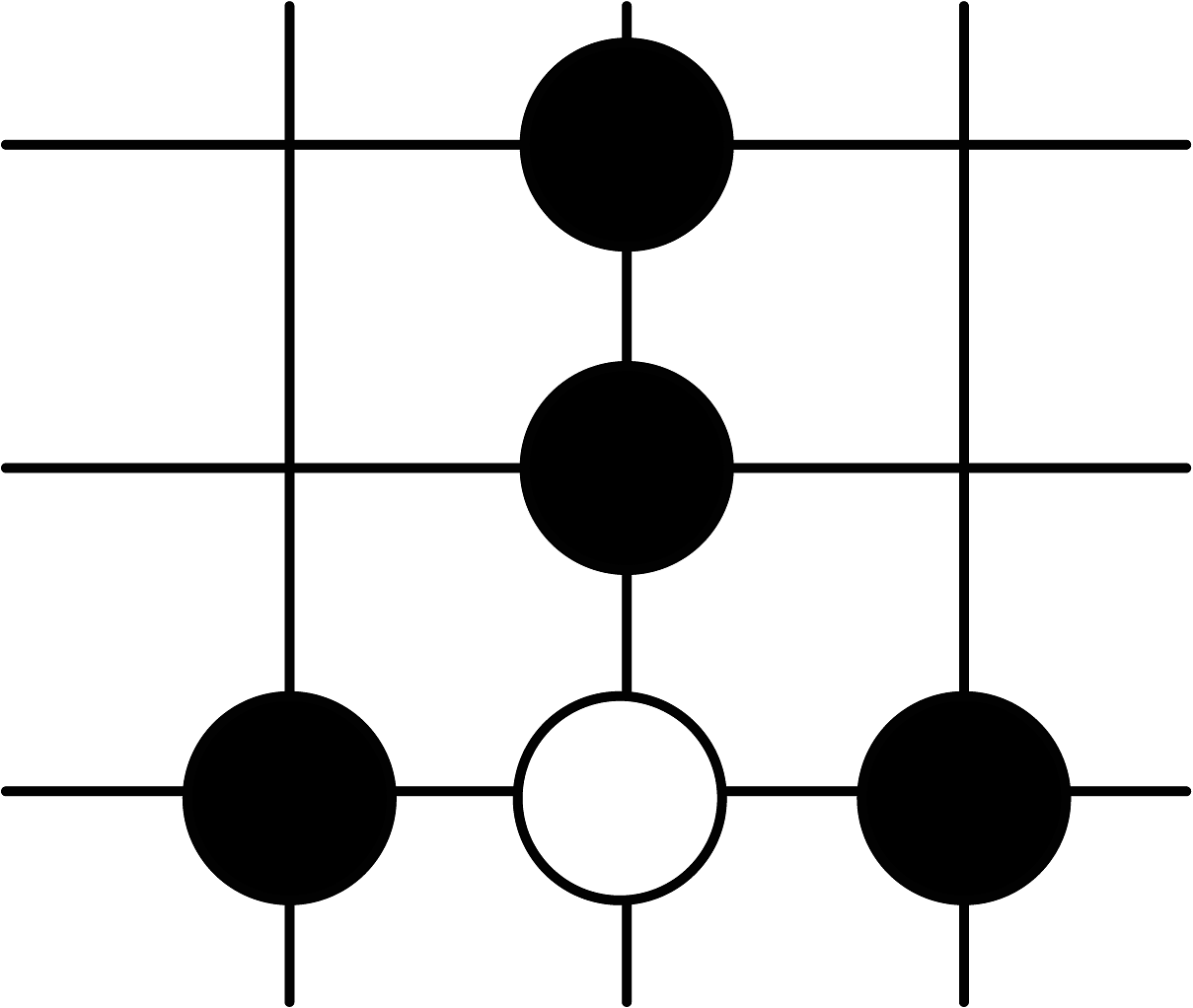
-
12、教科书第39页有下面一段文字:
思考:
如图1,把一长一短的两根木棍的一端固定在一起,摆出 . 固定住长木棍,转动短木棍,得到 . 这个实验说明了什么?
图1中的与满足两边和其中一边的对角分别相等,即 , , , 但与不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.

小明通过对上述问题的再思考,提出:两边和其中一边的对角(这个角是钝角)分别相等的两个三角形全等.即在和中,若 , , ( , 为钝角),则 . 对于小明的结论,阿强和阿芳分别提出了验证方案.
(1)、阿强的验证方案:根据教科书中探究三角形全等判定方法的经验,利用尺规作图验证小明提出的结论.即先画一个 , 使为钝角,如图2,再画一个 , 使 , , . 把画好的剪下来,放到上,看它们是否重合.请利用直尺和圆规画出符合条件的(不写画法,保留作图痕迹);
(2)、阿芳的验证方案:利用三角形全等的判定方法证明小明提出的结论.即:在和中,已知 , , ( , 为钝角),如图3.求证: . 请写出证明过程.

-
13、如图, , 是的角平分线, , 交于点E.请判断与的大小关系,并说明理由.

-
14、学习完《利用三角形全等测距离》后,数学兴趣小组同学就“测量河两岸A,B两点间距离”这一问题,设计了如下方案.
课题
测量河两岸A,B两点间距离
测量工具
测量角度的仪器,皮尺等
测量方案示意图

测量步骤
①在点B所在河岸同侧的平地上取点C和点D,使得点A,B,C在一条直线上,且;
②测得 , ;
③在的延长线上取点E,使得;
④测得的长度为30米.
请你根据以上方案求出A,B两点间的距离 .
-
15、某工厂要制作两边长分别为2米和4米,第三边长为奇数的三角形框架.(1)、设计小组可以设计几种不同规格的三角形框架,为什么?(2)、设计小组成员到建材市场收集数据如下:
铁条规格/米
2
3
4
5
6
单价/(元/根)
6
8
10
15
20
根据市场能购买到的铁条制作满足上述条件的三角形框架各一个(铁条长度可以切割,但不能拼接),求最少费用.
-
16、如图, , , , 在同一直线上, , , , , 若 , 求的度数.

-
17、如图,方格纸中每个小正方顶点上.
 (1)、请在图1中画出中边上的高和边上的中线 .(2)、请在图2中画出与关于直线成轴对称的图形 .
(1)、请在图1中画出中边上的高和边上的中线 .(2)、请在图2中画出与关于直线成轴对称的图形 . -
18、两组邻边分别相等的四边形叫做“筝形”,如图,四边形是一个筝形,其中 , , 得到如下结论:①;②;③ , 其中正确的结论有(填序号).

-
19、已知为等边三角形,为的高,点E在延长线上,且 , 若 , 则 .

-
20、判断一张纸带的两边 , 是否相互平行,提供了两种折叠与测量方案.方案Ⅰ:沿图1中虚线折叠,若测得 , 则 , 否则不平行;方案Ⅱ:先沿图2中折叠,展开后再沿折叠,若测得 , , 则 , 否则不平行.对于方案Ⅰ,Ⅱ,下列说法正确的是( )
 A、Ⅰ可行,Ⅱ不可行 B、Ⅰ不可行,Ⅱ可行 C、Ⅰ,Ⅱ都不可行 D、Ⅰ,Ⅱ都可行
A、Ⅰ可行,Ⅱ不可行 B、Ⅰ不可行,Ⅱ可行 C、Ⅰ,Ⅱ都不可行 D、Ⅰ,Ⅱ都可行