相关试卷

1、一元二次方程 $x (x - 3) = 3 - x$ 的根是（）

A、 $x = - 1$ B、 $x = 3$ C、 $x_{1} = - 1$ ， $x_{2} = 3$ D、 $x_{1} = 1$ ， $x_{2} = 2$

查看解析
2、一个自然数的立方，可以分裂成若干个连续奇数的和．例如： $2^{3}, 3^{3}$ 和 $4^{3}$ 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和，即 $2^{3} = 3 + 5; 3^{3} = 7 + 9 + 11$ ； $4^{3} = 13 + 15 + 17 + 19$ ；……；若 $6^{3}$ 也按照此规律来进行“分裂”，则 $6^{3}$ “分裂”出的奇数中，最小的奇数是．由此可得，当n为正整数时， ${(2 n + 1)}^{3}$ “分裂”出的奇数中，最大的奇数是．

查看解析
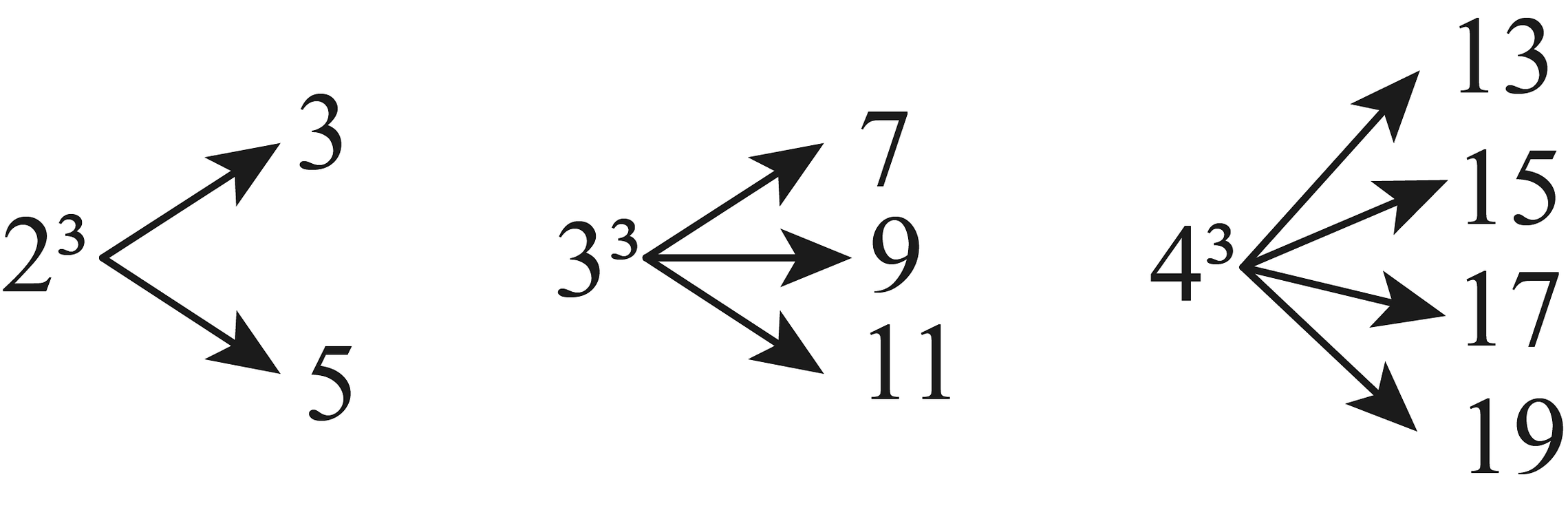
3、用小立方块搭一个几何体，使得它从正面看和从上面看到的形状图如图所示，它最少要 $m$ 个小立方块，最多要 $n$ 个小立方块，则 $m + n$ 的值为．

查看解析
4、绝对值小于2024的所有整数的积等于．

查看解析
5、在学习完“展开与折叠”后，老师让同学们用若干个正方形和长方形拼成一个长方体的展开图．拼完后，小军看来看去觉得所拼图形似乎存在问题．

(1)、请你帮小军分析一下拼图是否存在问题，若有多余块，则把图中多余块涂黑；若还缺少，则直接在原图中补全；

(2)、根据图中的数据，求出修正后的展开图所折叠而成的长方体的体积．

查看解析
6、（1）如果 $|a| = 6, |b| = 5$ 且 $a < b$ ，求 $b - a$ 的值；
（2）已知 $a, b$ 互为相反数， $c, d$ 互为倒数， $| m | = 2$ ，求代数式 $2 m - (a + b - 1) + 3 c d$ 的值．

查看解析
7、如图是由8个棱长均为 $1cm$ 的小正方体搭成的几何体，在下面的网格中画出这个几何体从正面、左面和上面看到的形状图．

(1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图；

(2)、在这个几何体上再添加一些相同的小正方体，如果从左面和从上面看到的形状图不变，那么最多可以再添加个小正方体；

(3)、计算这个几何体的表面积．

查看解析
8、计算下列各题：

(1)、 $27 - (- 12) + 3 - 7$ ；

(2)、 $(- 3 \frac{1}{3}) \times \frac{2}{5} \times (- 2 \frac{1}{2}) \div (- \frac{10}{7})$ ；

(3)、 $(- \frac{3}{4} - \frac{5}{9} + \frac{7}{12}) \div (- \frac{1}{36})$ ；

(4)、 $- 3^{2} + | - 7 | - {(- 2)}^{2} \times {(- 1)}^{2024}$ ．

查看解析
9、冰箱开始启动时的内部温度是12℃，如果每小时冰箱内部的温度降低5℃，那么4小时后，冰箱内部的温度是℃．

查看解析
10、如图是一个“数值转换机”，按下面的运算过程输入一个数x，若输入的数 $x = 3$ ，则输出的结果为（）

A、27 B、19 C、11 D、5

查看解析
11、已知直线 $y = - x + 2$ 与 $x$ 轴交于 $A$ ，与 $y$ 轴交于点 $B$ ，抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A, C$ 两点，与 $y$ 轴交于点 $B$

(1)、求这个抛物线的解析式

(2)、若 $P$ 是直线 $A B$ 上方抛物线上一点，存在点 $P$ 使得 $S_{△ A B P} = \frac{1}{4} S_{△ A B C}$ ，求点 $P$ 的坐标

(3)、在对称轴上是否存在点 $Q$ ，使得 $△ B O Q$ 的周长最小，若存在，请直接写出 $Q$ 点坐标，若不存在，请说明理由．

查看解析
12、如图，用长为 $24 m$ 的篱笆，一面利用墙（墙的最大长度 $a$ 为 $10 m$ ），围成中间隔有一道篱笆的长方形花圃．设花圃的宽 $A B$ 为 $x (m)$ ，面积为 $S (m^{2})$ ．

(1)、 $B C =$ 　　（用含 $x$ 的代数式表示）．

(2)、求出 $S$ 关于 $x$ 的函数表达式，并写出自变量的取值范围．

(3)、饲养室长 $x$ 为何值时，占地面积 $S$ 最大？并求出 $S$ 的最大值．

查看解析
13、如图，正方形 $A B C D$ 的边长为4，点 $F$ 与点 $E$ 是线段 $A B$ 与线段 $B C$ 上的两个动点，在运动过程中线段 $D F$ 与 $A E$ 始终保持垂直，则线段 $B G$ 的最小值是（　　）

A、 $\sqrt{5}$ B、2 C、 $\sqrt{5} - 2$ D、 $2 \sqrt{5} - 2$

查看解析
14、二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，对称轴为直线 $x = 1$ ，下列结论：① $b^{2} - 4 a c > 0$ ；② $a b c < 0$ ；③ $2 a + b = 0$ ；④ $4 a - 2 b + c > 0$ ；⑤ $a x^{2} + b x + c = 0$ 的解为 $x_{1} = - 1$ ， $x_{2} = 3$ ．其中正确的是（　　）

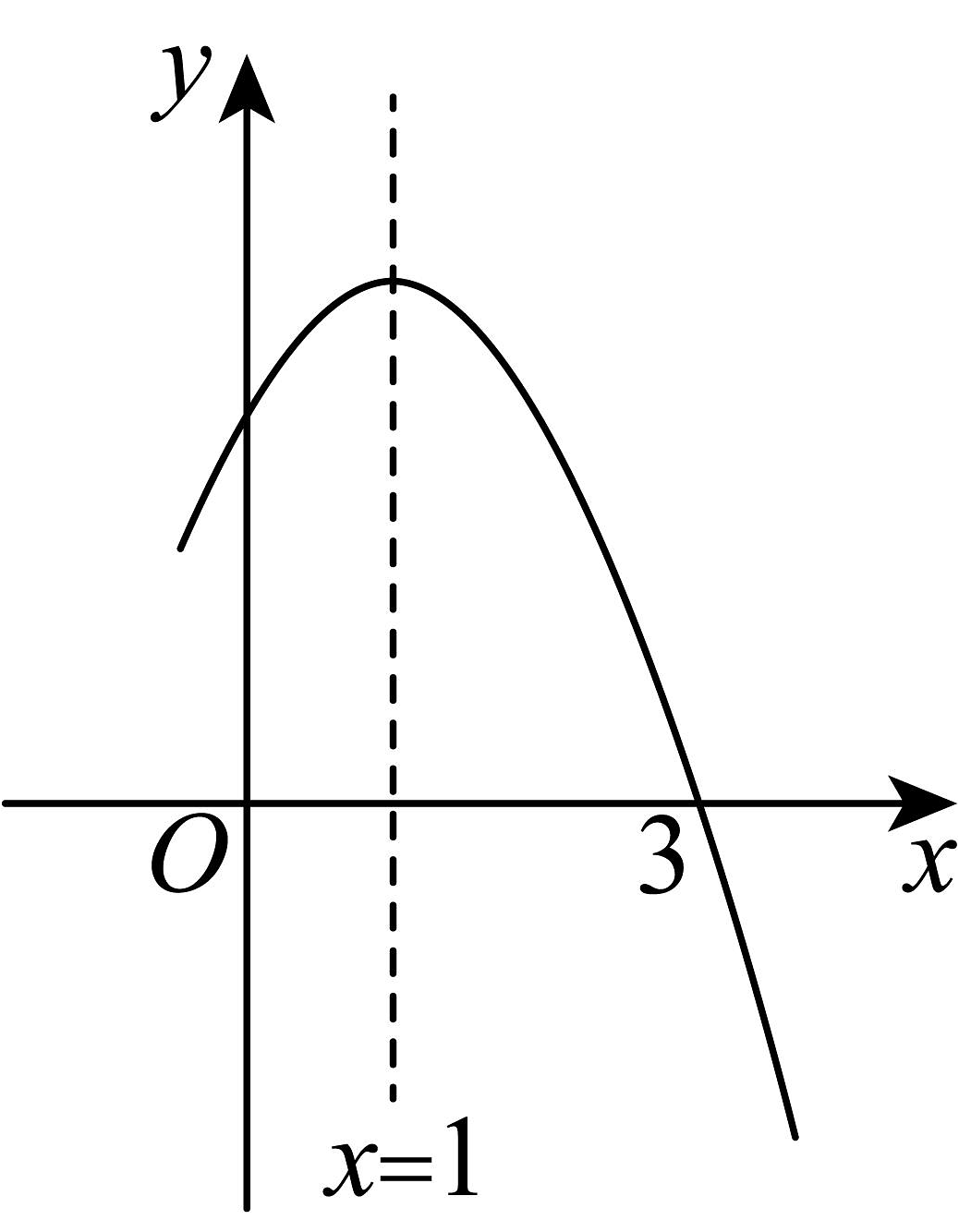A、①②③④ B、①③④⑤ C、①②③⑤ D、①②④⑤

查看解析
15、如图，已知 $⊙ O$ 的半径为 $5 cm$ ，弦 $A B$ 的长为 $8 cm$ ， P是 $A B$ 的延长线上一点， $B P = 2 cm$ ，则 $O P$ 等（）

A、 $2 \sqrt{3} cm$ B、 $3 \sqrt{3} cm$ C、 $2 \sqrt{5} cm$ D、 $3 \sqrt{5} cm$

查看解析
16、下列方程中是关于x的一元二次方程的是（）

A、 $x^{2} + 2 x = x^{2} + 1$ B、 $\frac{1}{x^{2}} + \frac{1}{x} - 2 = 0$ C、 $3 x + 2 y = 5$ D、 $3 {(x + 1)}^{2} = 2 x + 1$

查看解析
17、观察下列等式： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}, \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}, \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，将以上三个等式两边分别相加得 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$ ．

(1)、猜想并写出： $\frac{1}{n (n + 1)} =$ （用含n的代数式表示）；

(2)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2023 \times 2024} =$ ；

(3)、探究并计算： $\frac{1}{2 \times 4} + \frac{1}{4 \times 6} + \frac{1}{6 \times 8} + \dots + \frac{1}{2022 \times 2024}$ ．

查看解析
18、如图，观察下列几何体并回答问题：

(1)、 $n$ 棱柱有个面、条棱、个顶点， $n$ 棱锥有个面、条棱、个顶点．

(2)、所有像三棱柱、四棱柱、六棱柱、三棱锥等这样由四个或四个以上多边形所围成的立体图形叫作多面体．经过前人们归纳总结发现，多面体的面数 $F$ 、顶点个数 $V$ 以及棱的条数 $E$ 存在着一定的数量关系，请直接写出这个关系式．

查看解析
19、蒙古包，作为蒙古族传统的居住形式，承载着浓厚的游牧文化和历史底蕴．它的上面近似于圆锥形，下面近似于圆柱形．如图，一个蒙古包圆柱底面的周长是 $20 π$ 米，高是 $2$ 米，圆锥的高是 $1.2$ 米．

(1)、蒙古包的上面圆锥部分的侧面展开图是_______（填图形名称）；下面圆柱部分的侧面展开图是_______（填图形名称），圆柱部分的侧面展开图的面积是_____平方米（结果保留 $π$ ）．

(2)、这个蒙古包的体积是多少立方米？（结果保留 $π$ ）

查看解析
20、奥运会是集体育精神、民族精神和国际主义精神于一身的世界级运动盛会，象征着世界的和平、团结和友谊．今年巴黎奥运会虽在国外进行，但关注度仍然非常高，人们通过观看电视直播的方式关注这一体育盛会．据中国视听大数据调查显示，电视直播总观看户次超46亿，下表为8月份第一周的电视直播观看户次，其中7月31日观看户次为 $2.74$ 亿．（正数表示比前一天多的户次，负数表示比前一天少的户次）
日期
8月1日
8月2日
8月3日
8月4日
8月5日
8月6日
8月7日
奥运会电视直播观看户次/亿
$- 0.50$
$+ 0.35$
$+ 2.94$
$- 1.14$
$- 0.17$
$- 0.67$
$- 0.81$

(1)、8月2日的电视直播观看户次为亿．

(2)、这一周里，奥运会电视直播观看户次最多的一天达到亿，观看户次最少的一天达到亿．

(3)、据上表统计，这一周内奥运会电视直播总观看户次为多少亿？

查看解析

上一页 867 868 869 870 871 下一页跳转

日期	8月1日	8月2日	8月3日	8月4日	8月5日	8月6日	8月7日
奥运会电视直播观看户次/亿	$- 0.50$	$+ 0.35$	$+ 2.94$	$- 1.14$	$- 0.17$	$- 0.67$	$- 0.81$