相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、下列各式中,不相等的是( )A、和 B、和 C、和 D、和
-
2、有理数a,b,c在数轴上对应点如图所示,则下列式子中正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、下列计算错误的是( )A、 B、 C、 D、
-
4、将写成省略加号后的形式是( )A、 B、 C、 D、
-
5、若足球质量与标准质量相比,超出部分记作正数,不足部分记作负数,则在下面4个足球中,质量最接近标准的是( )A、
 B、
B、 C、
C、 D、
D、
-
6、在中,最小的数是( )A、 B、 C、 D、
-
7、用四舍五入法按要求对0.06018分别取近似值,其中错误的是( )A、0.1(精确到0.1) B、0.060(精确到0.001) C、0.06(精确到百分位) D、0.0602(精确到千分位)
-
8、方程的根的存在情况是( )A、有两个相等的实数根 B、有两个不相等的实根 C、没有实数根 D、无法确定
-
9、小明把一张长方形纸板的四周各剪去一个同样大小的小正方形,如图所示,长方形纸板的长为a,宽为b,小正方形的边长为c.
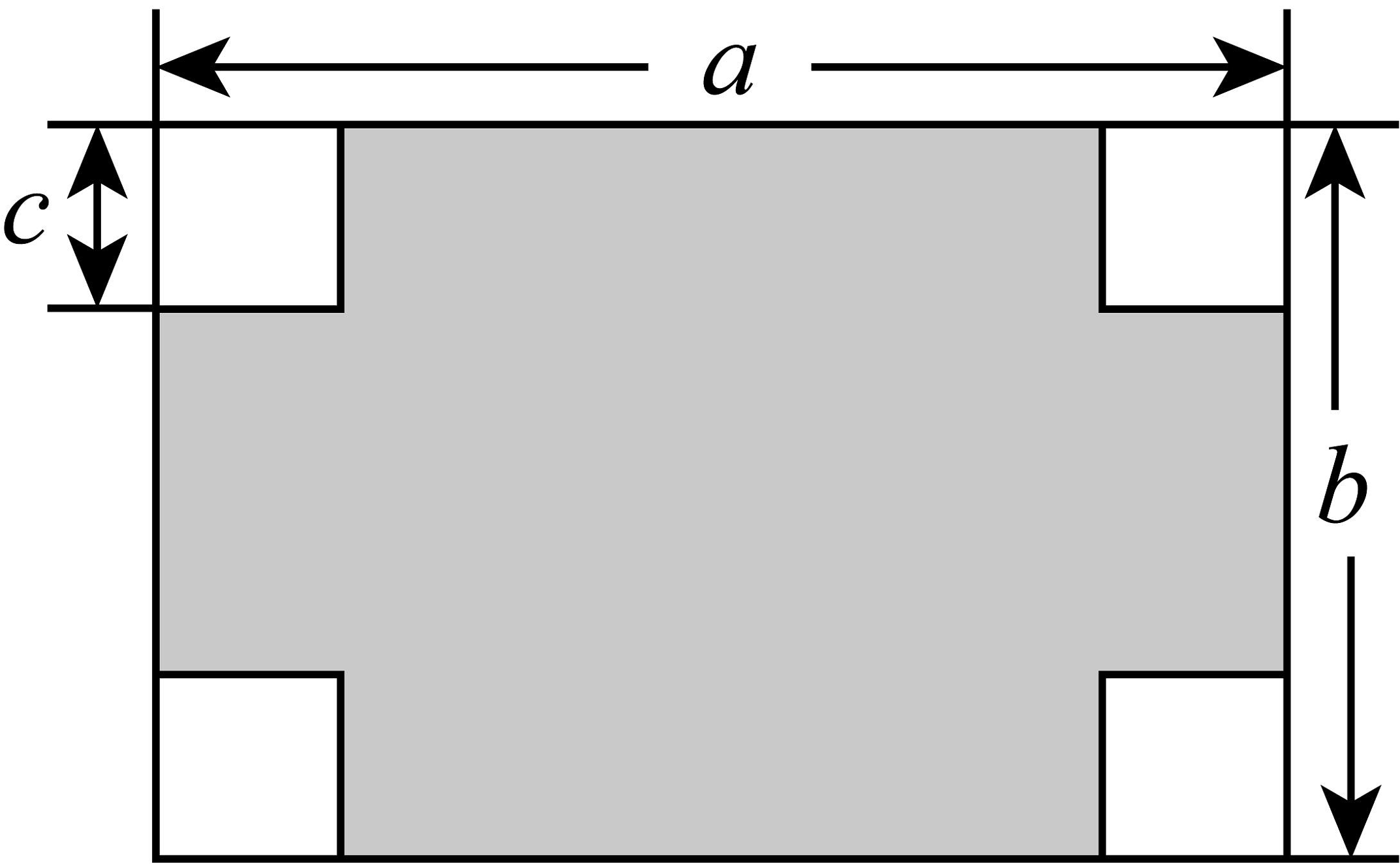 (1)、用含a、b、c的代数式表示剩余纸板(阴影部分)的面积.(2)、当时,求剩余纸板的面积.
(1)、用含a、b、c的代数式表示剩余纸板(阴影部分)的面积.(2)、当时,求剩余纸板的面积. -
10、已知多项式中不含项,求的值.
-
11、计算:(1)、 ;(2)、(3)、(4)、 .
-
12、同学们都知道,表示与的差的绝对值,实际上也可理解为与两数在数轴上所对应的两点之间的距离,同理可理解为与两数在数轴上所对应的两点之间的距离,则表示数轴上有理数所对应的点到和所对应的两点距离之和.请直接写出的最小值 .
-
13、若与是同类项,则 .
-
14、下列说法正确的有( )
①若 , 则;
②若 , 则有是正数;
③若代数式的值与无关,则该代数式值为;
④代数式最大值是 .
A、1个 B、2个 C、3个 D、4个 -
15、若 , 则的值为( )A、 B、 C、 D、
-
16、点在数轴上表示 , 把点沿数轴向左平移个单位到点 , 则点所表示的数是( )A、 B、 C、 D、或
-
17、已知抛物线与x轴相交于 , 两点,与y轴相交于点C.(1)、求抛物线的解析式;(2)、在抛物线的对称轴上是否存在一点P,使得的周长最小,若存在,请求出点P的坐标及的周长;若不存在,请说明理由;(3)、在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得?若存在,请求出点M的坐标;若不存在,请说明理由.
-
18、在平面直角坐标系中,为原点,点 , 点 , 若正方形绕点顺时针旋转,得正方形 , 记旋转角为 .
 (1)、如图 , 当时,求与的交点的坐标;(2)、如图 , 当时,求点的坐标;(3)、若为线段的中点,求长的取值范围(直接写出结果即可).
(1)、如图 , 当时,求与的交点的坐标;(2)、如图 , 当时,求点的坐标;(3)、若为线段的中点,求长的取值范围(直接写出结果即可). -
19、某商场购进一批单价为10元的日用品,若按每件20元的价格销售,每月能卖出20件,若按每件30元的价格销售,每月能卖出10件.假定每月销售件数y(件)与价格x(元/件)之间满足一次函数.(1)、试求y与x之间的函数关系.(2)、在不考虑其他因素的条件下,销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
-
20、如图,在中, , , 将绕B点逆时针旋转得到 , 旋转角为(),若三点恰好在同一条直线上;
 (1)、求旋转角的度数;(2)、若 , 求的长.
(1)、求旋转角的度数;(2)、若 , 求的长.